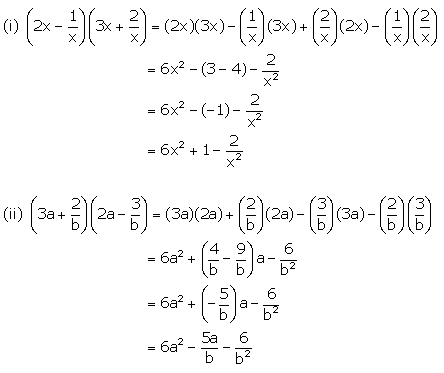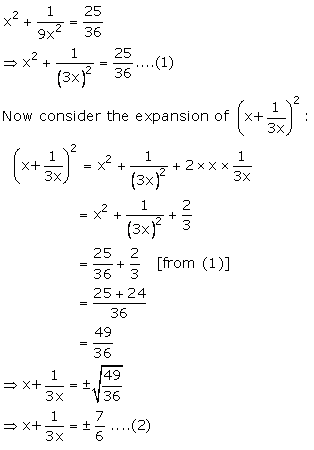Class 9 SELINA Solutions Maths Chapter 4: Expansion
Expansion Exercise Ex. 4(A)
Solution 1(a)
Correct option: (iii) 166
Substituting ![]() and
and ![]() in
in ![]() ,
,

Solution 1(b)
Correct option: (i) 11
Substituting ![]() and
and ![]() in
in ![]() ,
,
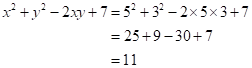
Solution 1(c)
Correct option: (iv) 7
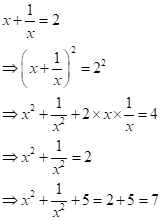
Solution 1(d)
Correct option: (ii) 58
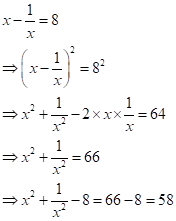
Solution 1(e)
Correct option: (iii) 84
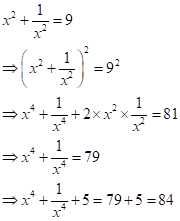
Solution 1(f)
Correct option: (i) 8
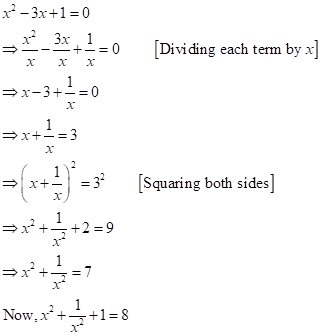
Solution 1(g)
Correct option:
(ii) ![]()
![]()
Now,
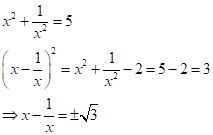
Solution 1(h)
Correct option:
(ii) ![]()
![]()
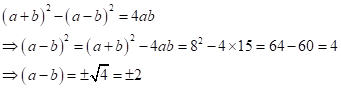
Now,
![]()
Solution 1(i)
Correct option: (ii) 2

Solution 2
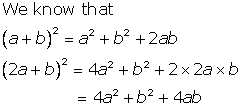


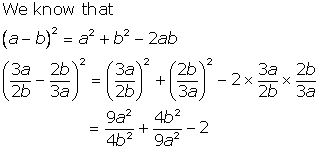
Solution 3
![]()

![]()

![]()

![]()
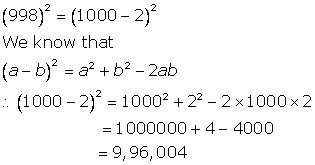
Solution 4
(i)
![]()

(ii)
![]()
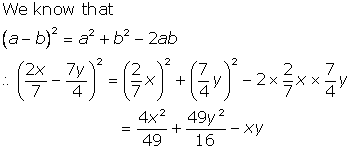
Solution 5
(i)Consider the given expression:

(ii)Consider the given expression:
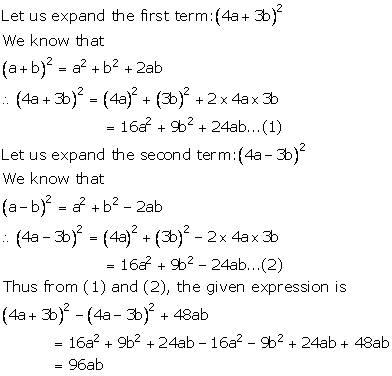
Solution 6

Solution 7

Solution 8
(i)

(ii)

Solution 9
(i)

(ii)

Solution 10
(i)

(ii)

Solution 11
(i)

(ii)

Solution 12
(i)

(ii)

Solution 13
(i)
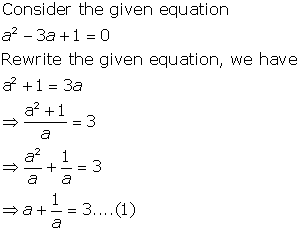
(ii)

Solution 14
(i)
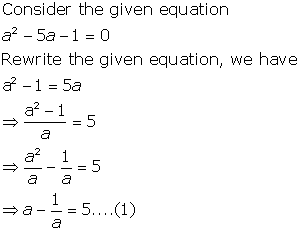
(ii)

(iii)

Solution 15

Solution 16
Given x is 2 more than y, so x = y + 2
Sum of squares of x and y is 34, so x2 + y2 = 34.
Replace x = y + 2 in the above equation and solve for y.
We get (y + 2)2 + y2 = 34
2y2 + 4y - 30 = 0
y2 + 2y - 15 = 0
(y + 5)(y - 3) = 0
So y = -5 or 3
For y = -5, x =-3
For y = 3, x = 5
Product of x and y is 15 in both the cases.
Solution 17
Let the two positive numbers be a and b.
Given difference between them is 5 and sum of squares is 73.
So a - b = 5, a2 + b2 = 73
Squaring on both sides gives
(a - b)2 = 52
a2 + b2 - 2ab = 25
But a2 + b2 = 73
So 2ab = 73 - 25 = 48
ab = 24
So, the product of numbers is 24.
Expansion Exercise Ex. 4(B)
Solution 1(a)
Correct option: (iv) 2

Solution 1(b)
Correct option: (ii) 90
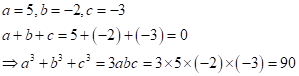
Solution 1(c)
Correct option: (i) 0
Given, ![]()
Now,
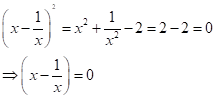
And,
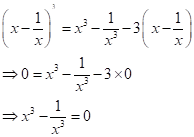
Solution 1(d)
Correct option: (iii)
![]()
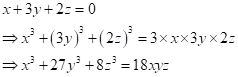
Solution 2
(i)

(ii)

(iii)

(iv)

Solution 3
(i)

(ii)

Solution 4
(i)
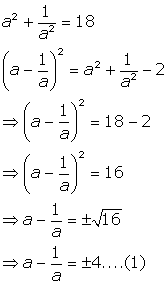
(ii)

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9
Property is if a + b + c = 0 then a3 + b3 + c3 = 3abc
(i) a = 13, b = -8 and c = -5
133 + (-8)3 + (-5)3 = 3(13)(-8)(-5) = 1560
(ii) a = 7, b = 3, c = -10
73 + 33 + (-10)3 = 3(7)(3)(-10) = -630
(iii)a = 9, b = -5, c = -4
93 - 53 - 43 = 93 + (-5)3 + (-4)3 = 3(9)(-5)(-4) = 540
(iv) a = 38, b = -26, c = -12
383 + (-26)3 + (-12)3 = 3(38)(-26)(-12) = 35568
Solution 10
(i)
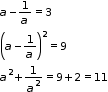
(ii)
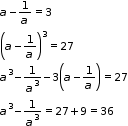
Solution 11
(i)

(ii)

(iii)

Solution 12

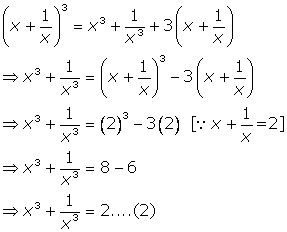

Thus from equations (1), (2) and (3), we have
![]()
Solution 13
Given that 2x - 3y = 10, xy = 16
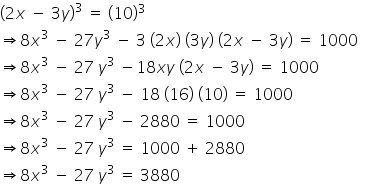
Solution 14
(i)
(3x + 5y + 2z) (3x - 5y + 2z)
= {(3x + 2z) + (5y)} {(3x + 2z) - (5y)}
= (3x + 2z)2 - (5y)2 [since (a + b) (a - b) = a2 - b2]
= 9x2 + 4z2 + 2 × 3x × 2z - 25y2
= 9x2 + 4z2 + 12xz - 25y2
= 9x2 + 4z2 - 25y2 + 12xz
(ii) (3x - 5y - 2z) (3x - 5y + 2z)
= {(3x - 5y) - (2z)} {(3x - 5y) + (2z)}
= (3x - 5y)2 - (2z)2{since(a + b) (a - b) = a2 - b2}
= 9x2 + 25y2 - 2 × 3x × 5y - 4z2
= 9x2 + 25y2 - 30xy - 4z2
= 9x2 +25y2 - 4z2 - 30xy
Solution 15
Given sum of two numbers is 9 and their product is 20.
Let the numbers be a and b.
a + b = 9
ab = 20
Squaring both sides,
(a + b)2 = 92
a2 + b2 + 2ab = 81
a2 + b2 + 40 = 81
So sum of squares is 81 - 40 = 41
Cubing both sides,
(a + b)3 = 93
a3 + b3 + 3ab(a + b) = 729
a3 + b3 + 60(9) = 729
a3 + b3 = 729 - 540 = 189
So the sum of cubes is 189.
Solution 16
Given x - y = 5 and xy = 24 (x>y)
(x + y)2 = (x - y)2 + 4xy = 25 + 96 = 121
So, x + y = 11; sum of these numbers is 11.
Cubing both sides,
(x - y)3 = 53
x3 - y3 - 3xy(x - y) = 125
x3 - y3 - 72(5) = 125
x3 - y3= 125 + 360 = 485
So, difference of their cubes is 485.
Cubing both sides, we get
(x + y)3 = 113
x3 + y3 + 3xy(x + y) = 1331
x3 + y3 = 1331 - 72(11) = 1331 - 792 = 539
So, sum of their cubes is 539.
Solution 17
xy = b ….(i)
4x2 + y2 = a ….(ii)
Now, (2x + y)2 = (2x)2 + 4xy + y2
= 4x2 + y2 + 4xy
= a + 4b ….[From (i) and (ii)]
![]()
Expansion Exercise Ex. 4(C)
Solution 1(a)
Correct option:
(ii) ![]()
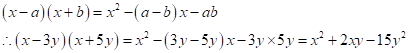
Solution 1(b)
Correct option:
(ii) ![]()
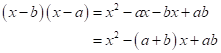
Solution 1(c)
Correct option: (ii) 1

Solution 1(d)
Correct option:
(iii) ![]()
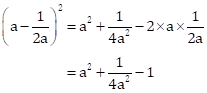
Solution 2
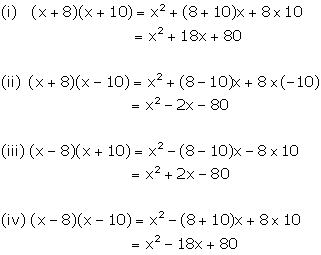
Solution 3
Solution 4
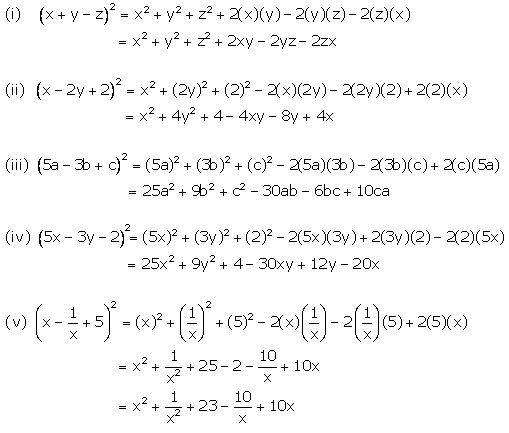
Solution 5

Solution 6

Solution 7

Solution 8

Solution 9
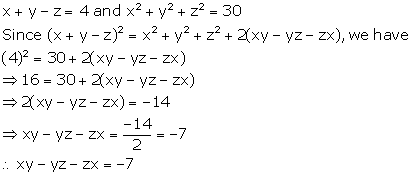
Expansion Exercise Ex. 4(D)
Solution 1(a)
Correct option: (i) 4
![]()
Now,
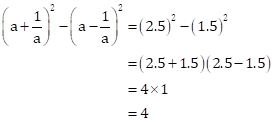
Solution 1(b)
Correct option: (iii) -10
![]()
Therefore, the coefficient of ![]() is -10.
is -10.
Solution 1(c)
Correct option:
(ii) ![]()
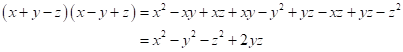
Solution 1(d)
Correct option: (i) -24
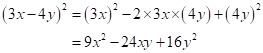
![]()
Solution 2
Given that x3 + 4y3 + 9z3 = 18xyz and x + 2y + 3z = 0
Therefore, x + 2y = - 3z, 2y + 3z = -x and 3z + x = -2y
Now

Solution 3
(i)
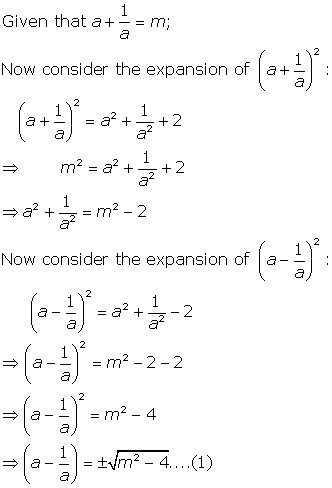
(ii)

Solution 4
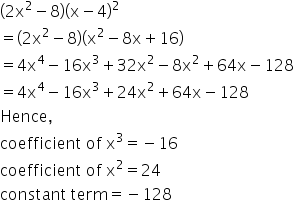
Solution 5
Given that
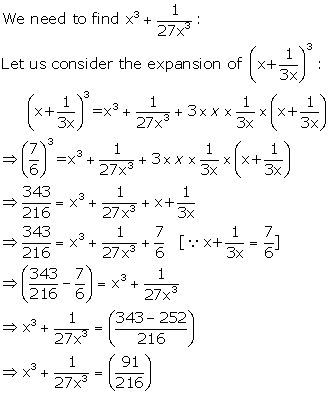
Solution 6
(i)
2(x2 + 1} = 5x
![]()
Dividing by x, we have

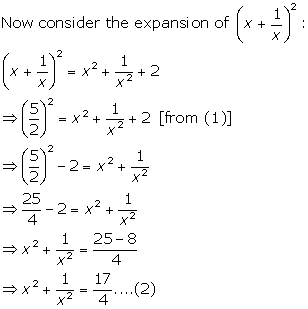
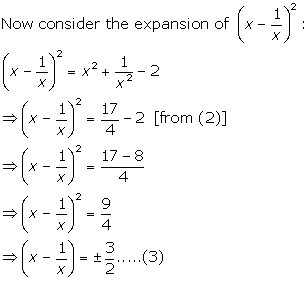
(ii)
![]()

Solution 7
a2 + b2 = 34, ab= 12
(a + b)2 = a2 + b2 + 2ab = 34 + 2 x 12 = 34 + 24 = 58
(a - b)2 = a2 + b2 - 2ab = 34 - 2 x 12 = 34- 24 = 10
(i) 3(a + b)2 + 5(a - b)2 = 3 x 58 + 5 x 10 = 174 + 50 = 224
(ii) 7(a - b)2 - 2(a + b)2 = 7 x 10 - 2 x 58 = 70 - 116 = -46
Solution 8
Given 3x - ![]()
We need to find![]()

Solution 9
Given that ![]()
We need to find the value of ![]()
Consider the given equation:
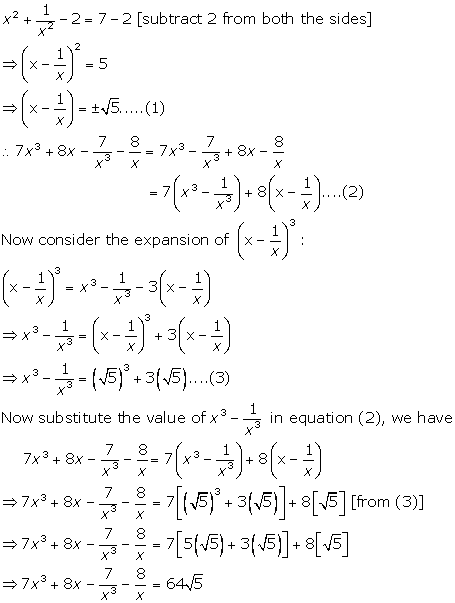
Solution 10
![]()
By cross multiplication,
=> x (x - 5) = 1 => x2 - 5x = 1 => x2 - 1 = 5x
Dividing both sides by x,


![]()
Solution 11
![]()
By cross multiplication,
=> x (5 - x) = 1 => x2 - 5x =-1 => x2 + 1 = 5x
Dividing both sides by x,


Solution 12
Given that 3a + 5b + 4c = 0
3a + 5b = -4c
Cubing both sides,
(3a + 5b)3 = (-4c)3
=>(3a)3 + (5b)3 + 3 x 3a x 5b (3a + 5b) = -64c3
=>27a3 + 125b3 + 45ab x (-4c) = -64c3
=> 27a3 + 125b3 - 180abc = -64c3
=> 27a3 + 125b3 + 64c3 = 180abc
Hence proved.
Solution 13
Let a, b be the two numbers.
.'. a + b = 7 and a3 + b3 = 133
(a + b)3 = a3 + b3 + 3ab (a + b)
=> (7)3 = 133 + 3ab (7)
=> 343 = 133 + 21ab => 21ab = 343 - 133 = 210
=> 21ab = 210 => ab= 2I
Now a2 + b2 = (a + b)2 - 2ab = 72 - 2 x 10 = 49 - 20 = 29
Solution 14
(i) 4x2 + ax + 9 = (2x + 3)2
Comparing coefficients of x terms, we get
ax = 12x
so, a = 12
(ii) 4x2 + ax + 9 = (2x - 3)2
Comparing coefficients of x terms, we get
ax = -12x
so, a = -12
(iii) 9x2 + (7a - 5)x + 25 = (3x + 5)2
Comparing coefficients of x terms, we get
(7a - 5)x = 30x
7a - 5 = 30
7a = 35
a = 5
Solution 15
Given
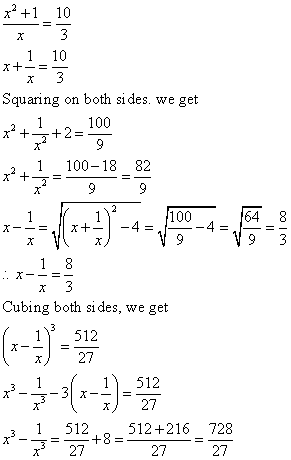
Solution 16
Given difference between two positive numbers is 4 and difference between their cubes is 316.
Let the positive numbers be a and b
a - b = 4
a3 - b3 = 316
Cubing both sides,
(a - b)3 = 64
a3 - b3 - 3ab(a - b) = 64
Given a3 - b3 = 316
So 316 - 64 = 3ab(4)
252 = 12ab
So ab = 21; product of numbers is 21
Squaring both sides, we get
(a - b)2 = 16
a2 + b2 - 2ab = 16
a2 + b2 = 16 + 42 = 58
Sum of their squares is 58.
Expansion Exercise Test Yourself
Solution 1
Using identity:
(x + a)(x + b)(x + c) = x3 + (a + b + c)x2 + (ab + bc + ca)x + abc
(i) (x + 6)(x + 4)(x - 2)
= x3 + (6 + 4 - 2)x2 + [6 × 4 + 4 × (-2) + (-2) × 6]x + 6 × 4 × (-2)
= x3 + 8x2 + (24 - 8 - 12)x - 48
= x3 + 8x2 + 4x - 48
(ii) (x - 6)(x - 4)(x + 2)
= x3 + (-6 - 4 + 2)x2 + [-6 × (-4) + (-4) × 2 + 2 × (-6)]x + (-6) × (-4) × 2
= x3 - 8x2 + (24 - 8 - 12)x + 48
= x3 - 8x2 + 4x + 48
(iii) (x - 6)(x - 4)(x - 2)
= x3 + (-6 - 4 - 2)x2 + [-6 × (-4) + (-4) × (-2) + (-2) × (-6)]x + (-6) × (-4) × (-2)
= x3 - 12x2 + (24 + 8 + 12)x - 48
= x3 - 12x2 + 44x - 48
(iv) (x + 6)(x - 4)(x - 2)
= x3 + (6 - 4 - 2)x2 + [6 × (-4) + (-4) × (-2) + (-2) × 6]x + 6 × (-4) × (-2)
= x3 - 0x2 + (-24 + 8 - 12)x + 48
= x3 - 28x + 48
Solution 2
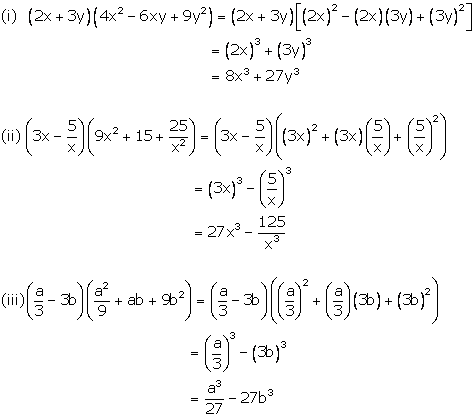
Solution 3
Using identity: (a ± b)3 = a3 ± b3 ± 3ab(a ± b)
(i) (104)3 = (100 + 4)3
= (100)3 + (4)3 + 3 × 100 × 4(100 + 4)
= 1000000 + 64 + 1200 × 104
= 1000000 + 64 + 124800
= 1124864
(ii) (97)3 = (100 - 3)3
= (100)3 - (3)3 - 3 × 100 × 3(100 - 3)
= 1000000 - 27 - 900 × 97
= 1000000 - 27 - 87300
= 912673
Solution 4

Solution 5

Solution 6
a3 - 8b3 + 27c3 = a3 + (-2b)3 + (3c)3
Since a - 2b + 3c = 0, we have
a3 - 8b3 + 27c3 = a3 + (-2b)3 + (3c)3
= 3(a)( -2b)(3c)
= -18abc
Solution 7
x + 5y = 10
⇒ (x + 5y)3 = 103
⇒ x3 + (5y)3 + 3(x)(5y)(x + 5y) = 1000
⇒ x3 + (5y)3 + 3(x)(5y)(10) = 1000
= x3 + (5y)3 + 150xy = 1000
= x3 + (5y)3 + 150xy - 1000 = 0
Solution 8
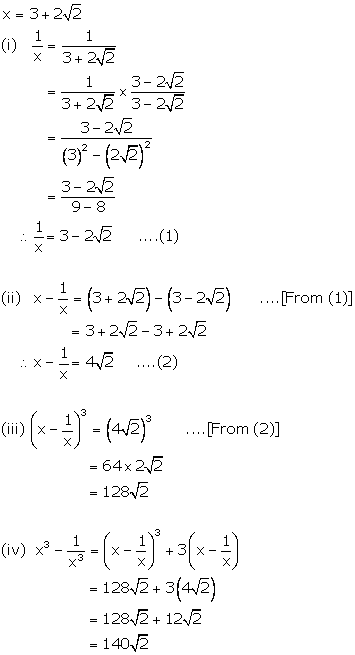
Solution 9
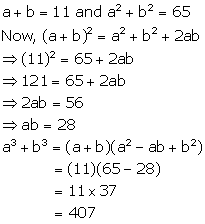
Solution 10
x2 + y2 + z2 - xy - yz - zx
= 2(x2 + y2 + z2 - xy - yz - zx)
= 2x2 + 2y2 + 2z2 - 2xy - 2yz - 2zx
= x2 + x2 + y2 + y2 + z2 + z2 - 2xy - 2yz - 2zx
= (x2 + y2 - 2xy) + (z2 + x2 - 2zx) + (y2 + z2 - 2yz)
= (x - y)2 + (z - x)2 + (y - z)2
Since square of any number is positive, the given equation is always positive.
Solution 11
(i) (a + b)(a + b) = (a + b)2
= a × a + a × b + b × a + b × b
= a2 + ab + ab + b2
= a2 + b2 + 2ab
(ii) (a + b)(a + b)(a + b)
= (a × a + a × b + b × a + b × b)(a + b)
= (a2 + ab + ab + b2)(a + b)
= (a2 + b2 + 2ab)(a + b)
= a2 × a + a2 × b + b2 × a + b2 × b + 2ab × a + 2ab × b
= a3 + a2 b + ab2 + b3 + 2a2b + 2ab2
= a3 + b3 + 3a2b + 3ab2
(iii) (a - b)(a - b)(a - b)
In result (ii), replacing b by -b, we get
(a - b)(a - b)(a - b)
= a3 + (-b)3 + 3a2(-b) + 3a(-b)2
= a3 - b3 - 3a2b + 3ab2