Class 9 SELINA Solutions Maths Chapter 28: Distance Formula
Distance Formula Exercise Ex. 28
Solution 1(a)
Correct option:
(iii) 
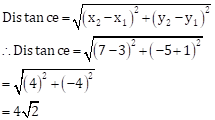
Solution 1(b)
Correct option: (i) 5 units
Solution 1(c)
Correct option: (iii) 3 or -9
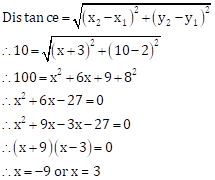
Solution 1(d)
Correct option: (iv) 3x + y = 5
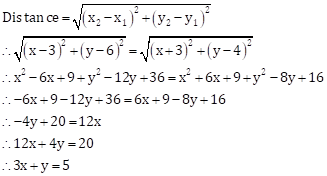
Solution 1(e)
Correct option: (i) 12 units
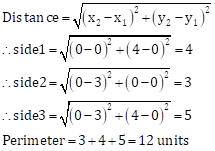
Solution 2
(i) (-3, 6) and (2, -6)
Distance between the given points
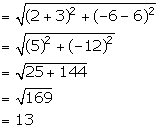
(ii) (-a, -b) and (a, b)
Distance between the given points
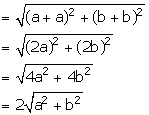
(iii) 
and 
Distance between the given points
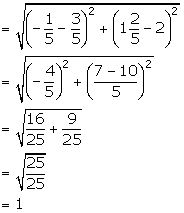
(iv) 
and 
Distance between the given points
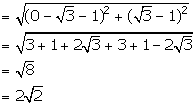
Solution 3
Coordinates of origin are O (0, 0).
(i) A (-8, 6)
AO = 
(ii) B (-5, -12)
BO = 
(iii) C (8, -15)
CO = 
Solution 4
It is given that the distance between the points A (3, 1) and B (0, x) is 5.
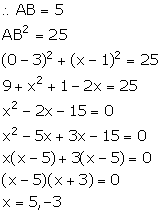
Solution 5
Let the coordinates of the point on x-axis be (x, 0).
From the given information, we have:
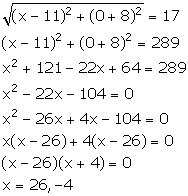
Thus, the required co-ordinates of the points on x-axis are (26, 0) and (-4, 0).
Solution 6
Let the coordinates of the point on y-axis be (0, y).
From the given information, we have:
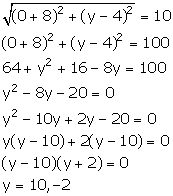
Thus, the required co-ordinates of the points on y-axis are (0, 10) and (0, -2).
Solution 7
It is given that the co-ordinates of point A are such that its ordinate is twice its abscissa.
So, let the co-ordinates of point A be (x, 2x).
We have:
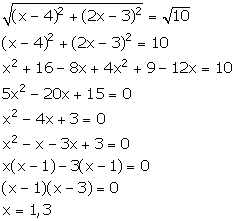
Thus, the co-ordinates of the point A are (1, 2) and (3, 6).
Solution 8
Given that the point P (2, -1) is equidistant from the points A (a, 7) and B (-3, a).
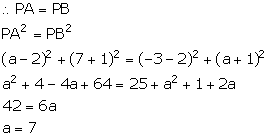
Solution 9
Let the co-ordinates of the required point on x-axis be P (x, 0).
The given points are A (7, 6) and B (-3, 4).
Given, PA = PB
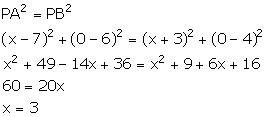
Thus, the required point is (3, 0).
Solution 10
Let the co-ordinates of the required point on y-axis be P (0, y).
The given points are A (5, 2) and B (-4, 3).
Given, PA = PB
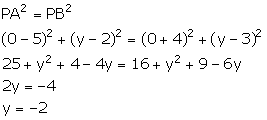
Thus, the required point is (0, -2).
Solution 11
(i) Since, the point P lies on the x-axis, its ordinate is 0.
(ii) Since, the point Q lies on the y-axis, its abscissa is 0.
(iii) The co-ordinates of P and Q are (-12, 0) and (0, -16) respectively.
PQ = 
Solution 12
Since, PQ = QR, 
PQR is an isosceles triangle.
Solution 13
Solution 14
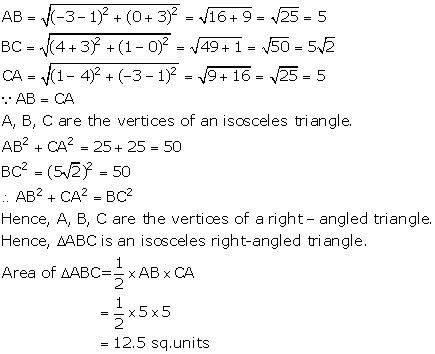
Solution 15
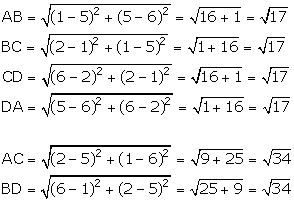
Since, AB = BC = CD = DA and AC = BD,
A, B, C and D are the vertices of a square.
Distance Formula Exercise Test Yourself
Solution 1
Point on y axis will be (0, y)
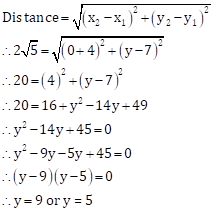
So points will be (0, 9) and (0, 5).
Solution 2
Solution 3
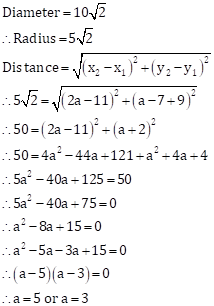
Solution 4
Let the given points be A (-3, 2), B (-5, -5), C (2, -3) and D (4, 4).
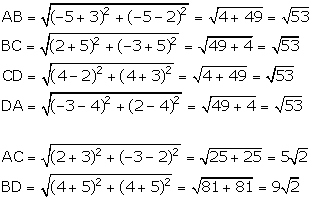
Since, AB = BC = CD = DA and AC 
BD
The given vertices are the vertices of a rhombus.
Solution 5
AB = CD
AB2 = CD2
(-6 + 3)2 + (a + 2)2 = (0 + 3)2 + (-1 + 4)2
9 + a2 + 4 + 4a = 9 + 9
a2 + 4a - 5 = 0
a2 - a + 5a - 5 = 0
a(a - 1) + 5 (a - 1) = 0
(a - 1) (a + 5) = 0
a = 1 or -5
It is given that a is negative, thus the value of a is -5.
Solution 6
Let the circumcentre be P (x, y).
Then, PA = PB
PA2 = PB2
(x - 5)2 + (y - 1)2 = (x - 11)2 + (y - 1)2
x2 + 25 - 10x = x2 + 121 - 22x
12x = 96
x = 8
Also, PA = PC
PA2 = PC2
(x - 5)2 + (y - 1)2 = (x - 11)2 + (y - 9)2
x2 + 25 - 10x + y2 + 1 - 2y = x2 + 121 - 22x + y2 + 81 - 18y
12x + 16y = 176
3x + 4y = 44
24 + 4y = 44
4y = 20
y = 5
Thus, the co-ordinates of the circumcentre of the triangle are (8, 5).
Solution 7
AB = 5
AB2 = 25
(0 - 3)2 + (y - 1 - 1)2 = 25
9 + y2 + 4 - 4y = 25
y2 - 4y - 12 = 0
y2 - 6y + 2y - 12 = 0
y(y - 6) + 2(y - 6) = 0
(y - 6) (y + 2) = 0
y = 6, -2
Solution 8
AB = 17
AB2 = 289
(11 - x - 2)2 + (6 + 2)2 = 289
x2 + 81 - 18x + 64 = 289
x2 - 18x - 144 = 0
x2 - 24x + 6x - 144 = 0
x(x - 24) + 6(x - 24) = 0
(x - 24) (x + 6) = 0
x = 24, -6
Solution 9
Distance between the points A (2x - 1, 3x + 1) and B (-3, -1) = Radius of circle
AB = 10 (Since, diameter = 20 units, given)
AB2 = 100
(-3 - 2x + 1)2 + (-1 - 3x - 1)2 = 100
(-2 - 2x)2 + (-2 - 3x)2 = 100
4 + 4x2 + 8x + 4 + 9x2 + 12x = 100
13x2 + 20x - 92 = 0
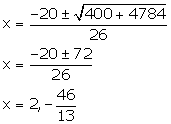
Solution 10
Let the co-ordinates of point Q be (10, y).
PQ = 10
PQ2 = 100
(10 - 2)2 + (y + 3)2 = 100
64 + y2 + 9 + 6y = 100
y2 + 6y - 27 = 0
y2 + 9y - 3y - 27 = 0
y(y + 9) - 3(y + 9) = 0
(y + 9) (y - 3) = 0
y = -9, 3
Thus, the required co-ordinates of point Q are (10, -9) and (10, 3).
Solution 11
(i) Given, radius = 13 units
PA = PB = 13 units
Using distance formula,
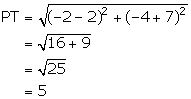
Using Pythagoras theorem in 
PAT,
AT2 = PA2 - PT2 = 169 - 25 = 144
AT = 12 units
(ii) We know that the perpendicular from the centre of a circle to a chord bisects the chord.
AB = 2AT = 2 
12 units = 24 units
Solution 12
Solution 13
We know that any point on x-axis has coordinates of the form (x, 0).
Abscissa of point B = 11
Since, B lies of x-axis, so its co-ordinates are (11, 0).
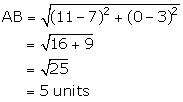
Solution 14
We know that any point on y-axis has coordinates of the form (0, y).
Ordinate of point B = 9
Since, B lies of y-axis, so its co-ordinates are (0, 9).
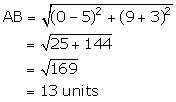
Solution 15
Let the required point on y-axis be P (0, y).
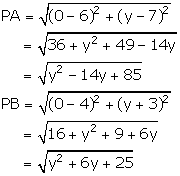
From the given information, we have:
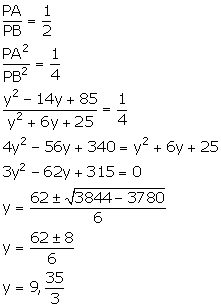
Thus, the required points on y-axis are (0, 9) and
.
Solution 16
It is given that PA: PB = 2: 3
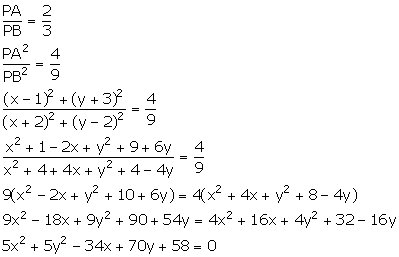
Hence, proved.
Solution 17
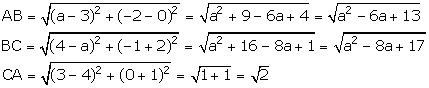
Since, triangle ABC is a right-angled at A, we have:
AB2 + AC2 = BC2
a2 - 6a + 13 + 2 = a2 - 8a + 17
2a = 2
a = 1