Class 9 SELINA Solutions Maths Chapter 15 - Construction of Polygons (Using ruler and compass only)
Construction of Polygons (Using ruler and compass only) Exercise Ex. 15
Solution 1(a)
Correct option: (ii) four sides and one angle are known
A quadrilateral can be constructed if its four sides and one angle are known.
Solution 1(b)
Correct option: (iv) two adjacent sides and contained angle are known
A parallelogram can be constructed if two consecutive sides and the included angle are given.
Solution 1(c)
Correct option: (i) two diagonals and included angle are given
A parallelogram can be constructed if its two diagonals and the included angle are given.
Solution 1(d)
Correct option: (iii) four sides and parallel sides are given
A trapezium can be constructed if its four sides and parallel sides are given.
Solution 1(e)
Correct option: (ii) one side and one diagonal are given
A rhombus can be constructed if measure of its one side and one diagonal are given.
Also, a rhombus can be constructed if both the diagonals are given.
Solution 2
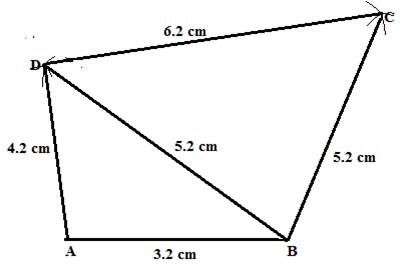
Steps:
1. Draw ![]() .
.
2. With A as a centre draw an arc at D and with B as a centre and radius 5.2 cm draw an arc at D.
3. join AD and DB.
4. With D and b as a centre taking radius 6.2 cm and 5.2 cm draw arc at C. Now join BC and DC.
ABCD is the required quadrilateral.
Solution 3
Steps:
1. Draw ![]() .
.
2. Through A draw AP such that ![]() .
.
3. From AP cut ![]()
4. With D and B as centre and radii 6.3 cm and 5.8 cm respectively, draw arcs cutting each other at C.
5. Join DC and BC.
ABCD is the required quadrilateral.
Solution 4
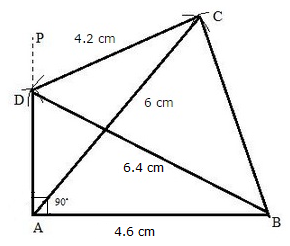
Steps:
1. Draw AB = 4.6 cm
2. Through A, draw AP such that Angle A = 90°.
3. With B as a centre and radii 6.4 cm draw an arc at D on AP.
4. With D and A as a centre and radii 4.2 cm and 6 cm draw arc cutting each other at C.
5. Now join BD, AC and CB.
ABCD is the required quadrilateral.
Solution 5
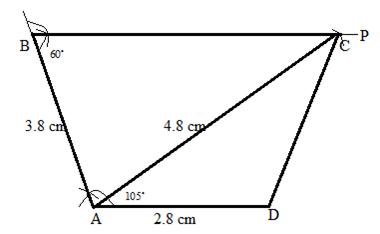
Steps:
1. Draw ![]()
2. Draw ![]() and
and ![]() .
.
3. draw BP such that ![]() .
.
4. With A as a centre and radii 4.8 cm draw an arc cutting BP at C.
5. Join AC,AD.
ABCD is the required quadrilateral.
Solution 6
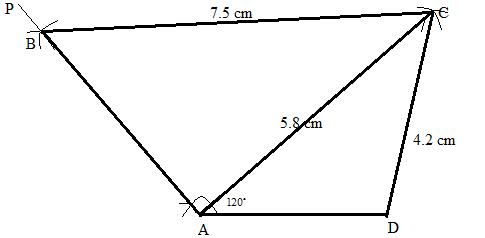
Steps:
1. Draw ![]()
2. draw AP such that ![]() .
.
3. With A and D as a centre and radii 5.8 cm and 4.2 cm draw arcs cutting each other at C.
4. Now join AC and CD.
5. Now with C as centre and radii 7.5 cm draw an arc at B on AP.
6. Now join CB.
ABCD is the required quadrilateral.
Solution 7
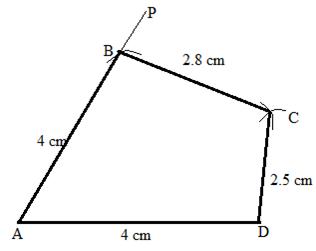
Steps:
1. Draw ![]()
2. Draw AP such that ![]() .
.
3. With A as a centre with radii 4 cm draw an arc at B on AP.
4. Now taking B and D as a centre and radii 2.8 cm and 2.8 cm draw arcs cutting each other at C.
5. Now join BC and CD.
ABCD is the required quadrilateral.
Solution 8
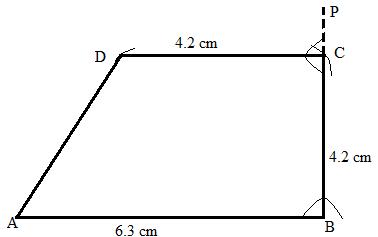
Steps:
1. draw ![]()
2. Draw BP such that ![]() .
.
3. With B as a centre and radii 4.2 cm draw an arc AP at C.
4. With C as a centre draw a line CD with radii 4.2 cm draw a line such that ![]() .
.
5. Now join AD
ABCD is the required quadrilateral.
Solution 9
Steps:
1. Draw ![]()
2. Draw triangle ACD.
3. Then draw triangle ABC.
ABCD is the required parallelogram.
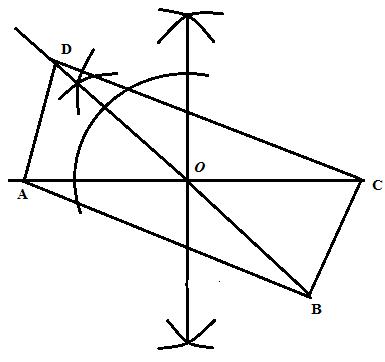
Solution 10
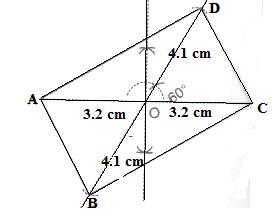
Steps:
1. Draw ![]()
2. Draw line BOD such that ![]() and
and ![]()
3. Join AB,BC,CD and DA.
ABCD is the required parallelogram.
Solution 11
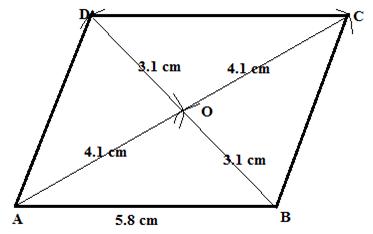
Steps:
1. Since diagonal of a parallelogram bisect each other, construct OAB such that ;
And ![]()
2. Produce AO up to C, such that ![]() and BO upto D, such that
and BO upto D, such that ![]() .
.
3. Join AD,DC and CB.
ABCD is the required parallelogram.
Solution 12
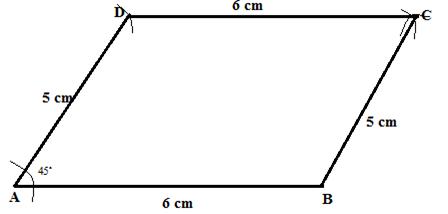
Steps:
1. Draw ![]()
2. Draw AD with radii 5 cm with an angle of ![]() .
.
3. With D and B as a centre and radii 6 cm and 5cm draw arcs cutting each other at C.
4. Now join DC and BC.
ABCD is the required parallelogram.
Solution 13
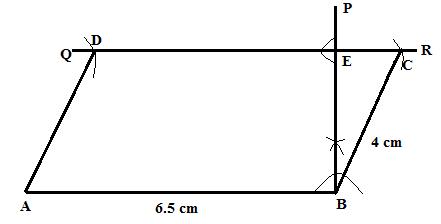
Steps:
1. Draw ![]()
2. At B, draw ![]()
3. From BP cut ![]() .
.
4. Through E draw perpendicular to BP to get QR parallel to AB.
5. With B as a centre and radius ![]() ,draw an arc which cuts QR at C.
,draw an arc which cuts QR at C.
6. With A as a centre and radius ![]() ,draw an arc which cuts QR at D.
,draw an arc which cuts QR at D.
ABCD is the required parallelogram.
Solution 14
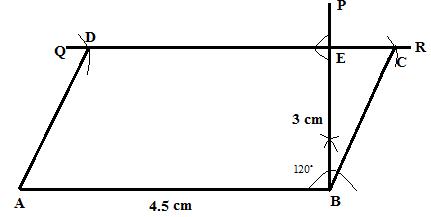
Steps:
1. Draw ![]()
2. At B, draw ![]()
3. From BP cut ![]() .
.
4. Through E draw perpendicular to BP to get QR parallel to AB.
5. With B as a centre draw an arc which cuts QR at C.
6. With A as a centre draw an arc which cuts QR at D.
7. Now join Ad and BC.
ABCD is the required parallelogram.
Solution 15
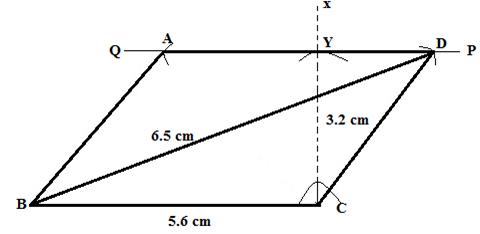
Steps:
1. Draw ![]() .
.
2. At C, draw CX perpendicular to BC.
3. with C as a centre and taking radius 3.2 cm draw an arc to cut CX at Y.
4. Through Y draw a straight line PQ parallel to BC.
5. With B as a centre and radius 6.5 cm draw an arc to meet PQ at D.
6. With D as a centre and radius equal to 5.6 cm , draw an arc to meet PQ at A.
7. Join BA,BD and CD.
ABCD is the requiredparallelogram.
Solution 16
Since each angle of a rectangle is ![]() and opposite sides are equal. Therefore,
and opposite sides are equal. Therefore,

Steps:
1. Draw BC = 7.2 cm.
2. with B as a centre draw a line BX taking as a ![]()
3. Now taking radius 6 cm draw an arc at A.
4. From point A draw a line AY parallel to BC.
5. With A as a centre taking radius 7.2 cm draw an arc at D.
6. Now join CD.
ABCD is the required rectangle.
Solution 17
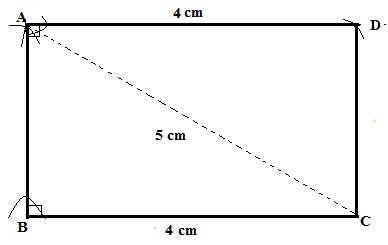
Steps:
1. Draw ![]() .
.
2. With C as a centre and radius 5 cm draw an arc at A.
3. Now join AB and AC.
4. With A as a centre draw an arc at D.
5. Now join AD and CD.
ABCD is the required rectangle.
Solution 18

Steps:
1. Draw ![]() .
.
2. Draw right triangle ACB.
3. Draw right triangle ADB.
4. Join DC.
ABCD is the required rectangle.
Solution 19
Given that the base = 4.8 cm2 and Area = ![]()
We know that area of rectangle![]() .
.
Therefore,
24 = 4.8 x height
Height= 5
With ![]() and height
and height ![]() , the rectangle is shown below:
, the rectangle is shown below:
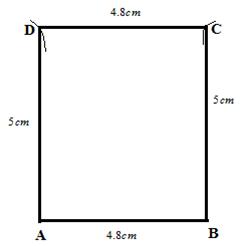
Steps:
1. Draw base ![]() .
.
2. With A and B as a centre draw an arcs taking radius ![]() at D and C.
at D and C.
3. Now join AD,BC and DC.
ABCD is the required rectangle.
Solution 20
Given that the height = 4.5 cm and Area = ![]()
We know that area of rectangle![]() .
.
Therefore,
36= base x 4.5
Base= 8 cm
With ![]() and base
and base ![]() , the rectangle is shown below:
, the rectangle is shown below:

Steps:
1. Draw base ![]() .
.
2. With A and B as a centre draw an arcs taking radius ![]() at D and C.
at D and C.
3. Now join AD,BC and DC.
ABCD is the required rectangle.
Solution 21
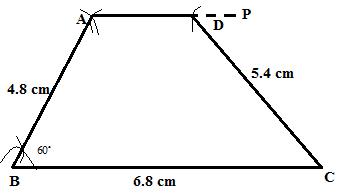
Steps:
1. Draw![]() .
.
2. With B as a centre and radii 4.8 cm draw an arc at A such that ![]() .
.
3. From point A draw a line AP such that ![]() .
.
4. With C as a centre and radii 5.4 cm draw an arc at D on the line AP.
5. Now join AB,CD.
ABCD is the required trapezium.
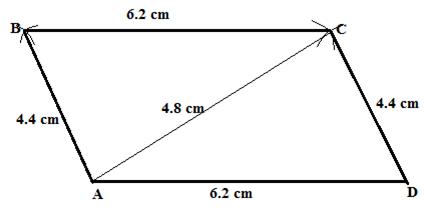
Solution 22
Steps:
1. Draw ![]() .
.
2. From BC cut BE = AD = 4.4 cm
3. draw triangle DEC such that
![]() and
and ![]() .
.
4. Taking B and D as a centre and radii 3.2 cm and 4.4 cm respectively, draw arcs cutting each other at A.
5. Join AB and AD.
ABCD is the required trapezium.
Solution 23
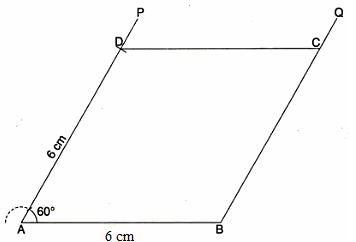
Steps:
1. Draw a line ![]()
2. At A, we construct![]() .
.
3. From AP, we cut at D taking![]() .
.
4. Through B, we draw![]() .
.
5. through D, we draw ![]() to cut BQ at C.
to cut BQ at C.
ABCD is the required rhombus.
Solution 24
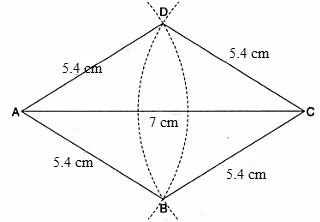
Steps:
1. We construct the segment ![]() .
.
2. With A as a centre and radius 5.4 cm , we draw an arc extending on both sides of AC.
3. With C as centre and same radius as in step 2, we draw an arc extending on both sides of AC to cut the first arc at B and D.
4. Join AB,BC,CD and DA.
ABCD is the required rhombus.
Solution 25
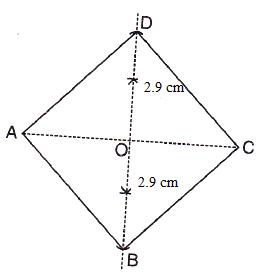
Steps:
1. Draw ![]() .
.
2. Draw perpendicular bisector to AC which cuts AC at O.
3. From this perpendicular cut OD and OB such that,
![]()
4. Join AB,BC,CD and DA.
ABCD is the required rhombus.
Solution 26
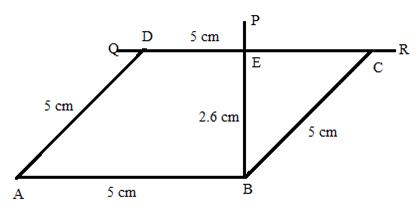
Steps:
1. Draw ![]()
2. At B, draw ![]() .
.
3. From BP, cut ![]()
4. Through E draw perpendicular to CP to get QR parallel to AB.
5. With A and B as a centre and radii 5 cm draw arcs cutting QR at D and C.
ABCD is the required rhombus.
Solution 27
- Construct ∠XAY = 60o
- Then draw a perpendicular ZA = 3cm from A
- Now from Z draw a perpendicular that will meet XA at B
- Take radius equal to AB and cut an arc on AY from A to get point D
- Now keeping the radius as AB, cut arcs from B and D to get the point C
- Now join BC and DC to get the required rhombus ABCD
Solution 28
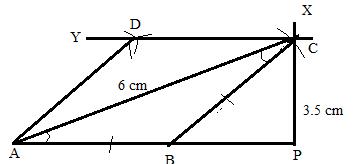
Steps:
1. draw a line AP.
2. now draw ![]() and
and ![]()
3. Now draw a line BC such that ![]() .
.
4. Now at C draw a line CY parallel to AP.
5. At point C and A, taking radius same as AB draw arcs cutting each other at D.
6. Now join AD.
ABCD is the required rhombus.
Solution 29
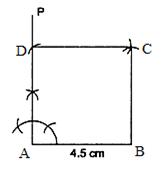
Steps:
1. Draw a line segment ![]()
2. Draw ![]() .
.
3. From AP cut off ![]() .
.
4. With B as a centre and radius 4.5 cm draw an arc.
5. With D as centre and radius 4.5 cm draw another arc cutting the former arc at C.
6. Join BC and CD.
ABCD is the required square.
Solution 30
We know that the diagonals of a square are equal and bisect each other at right angles.
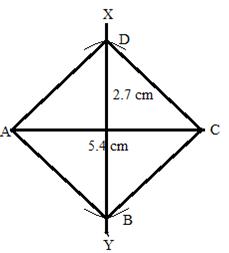
Steps:
1. draw ![]()
2. Draw the right bisector XY of AC, meeting AC at O.
3. From O, set off ![]() along OY and
along OY and ![]() along OX.
along OX.
4. Join AB, BC, CD and DA.
ABCD is the required square.
Solution 31
The perimeter of a square
![]()
Where a is the length of each side.
We have Perimeter = 24 cm.
Therefore,
![]()
Therefore the sides of the squares are of length 6 cm.
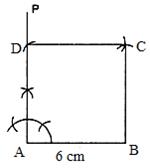
Steps:
1. Draw a line segment ![]()
2. Draw ![]() .
.
3. From AP cut off ![]() .
.
4. With B as a centre and radius 6 cm draw an arc.
5. With D as centre and radius 6 cm draw another arc cutting the former arc at C.
6. Join BC and CD.
ABCD is the required square.
Solution 32
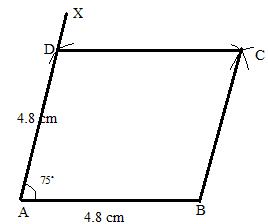
Steps:
1.draw a line ![]()
2. At A Draw AX such that ![]() .
.
3. With A as a centre and measurement equal to AB cut off an arc at D on AX.
4. Using same radius taking D and B as centers cut off arcs, which will intersect at C.
5. Join CD and CB.
ABCD is the required rhombus.
Solution 33(i)
The length of side of regular hexagon is equal to the radius of its circumcircle.
Steps of construction:
1. Draw a circle of radius 2.5 cm
2. Taking any point A on the circumference of the circle as centre, draw arcs of same radii (i.e. 2.5 cm) which cut the circumference at B and F.
3. With B and F as centres, again draw two arcs of same radii which cut the circumference at C and E respectively.
4. With C or E as centre, draw one more arc of the same radius which cuts the circumference at point D.
In this way, the circumference of the circle is divided into six equal parts.
5. Join AB, BC, CD, DE, EF and FA.
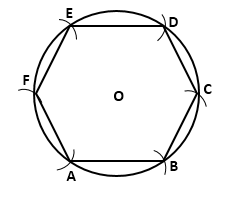
ABCDEF is the required regular hexagon.
Solution 33(ii)
The length of side of regular hexagon is equal to the radius of its circumcircle.
Steps of construction:
1. Draw a circle of radius 3.2 cm
2. Taking any point A on the circumference of the circle as centre, draw arcs of same radii (i.e. 3.2 cm) which cut the circumference at B and F.
3. With B and F as centres, again draw two arcs of same radii which cut the circumference at C and E respectively.
4. With C or E as centre, draw one more arc of the same radius which cuts the circumference at point D.
In this way, the circumference of the circle is divided into six equal parts.
5. Join AB, BC, CD, DE, EF and FA.
ABCDEF is the required regular hexagon.
Construction of Polygons (Using ruler and compass only) Exercise Test Yourself
Solution 1
Steps of construction:
1) Draw AB = 7 cm.
2) Through B, draw BX such that ∠ABX = 90o.
3) From BX, cut BC = 5 cm.
4) Through C, draw CY such that ∠BCY = 90o.
5) From CY, cut CD = 5 cm.
6) Join AD.
ABCD is the required quadrilateral.
Solution 2
Steps of construction:
1) Draw BC = 5 cm.
2) From BC, cut BE = 4.5 cm.
3) Draw triangle DEC such that DE = AB = 3.6 cm and CD = 3.6 cm.
4) Taking B and D as centres and radii 3.6 cm and 4.5 cm respectively, draw arcs cutting each other at A.
5) Join AB and AD.
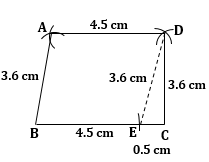
ABCD is the required trapezium.
Solution 3
Steps of construction:
1) Draw AB = 5 cm.
2) Through B, draw BX such that ∠ABX = 90o.
3) From BX, cut BC = 3.6 cm.
4) Through A, draw AY such that ∠BAY = 90o.
5) From AY, cut AD = 3.6 cm.
6) Join CD.
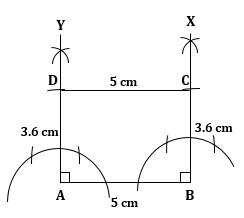
ABCD is the required rectangle.
Solution 4
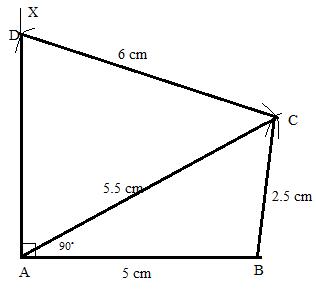
Steps:
1. draw ![]()
2. Now draw ![]() such that it is
such that it is ![]() .
.
3. Taking A and B as a centre and radius 2.5 cm and 5.5 cm draw arcs cuts off at C.
4. Now join BC and AC.
5. Taking C as a centre and radius 6 cm draw arcs at D on AX.
ABCD is the required quadrilateral.
Solution 5
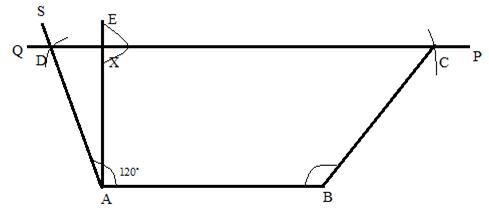
Steps:
1. Draw ![]() .
.
2. now draw ![]() and draw
and draw ![]() such that
such that ![]() .
.
3. Through X draw draw a line QR which is parallel to AB which cuts AS at D.
4. Through B draw an arc taking radius 3.6 cm at C on PQ.
5. Join CB.
ABCD is the required trapezium.
Solution 6
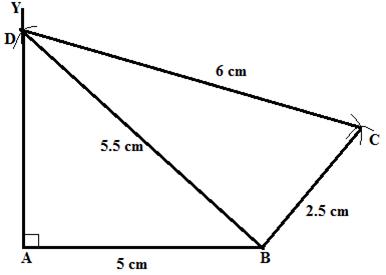
Steps:
1.Draw AB=5cm.
2. From A draw a line AY such that ![]() .
.
3. Taking B as a centre with radius 5.5 cm draw an arc at D on AY.
4. With D and B as centre and radii 6 cm and 2.5 cm draw arcs cutting each other at C.
4. Join DC and BC.
ABCD is the required quadrilateral.
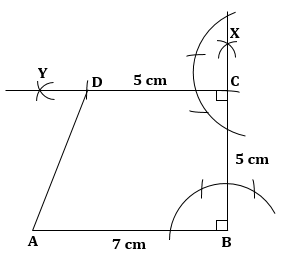
Solution 7

Steps:
1.draw AB=6cm.
2. With A as a centre draw a line AX such that ![]() .
.
3. With A as a centre and radii 3 cm draw an arc on AD.
4. now with D and B as a centre and radii 6 cm and 3 cm draw arcs cutting each other at C.
5. Join DC and BC.
ABCD is the required parallelogram.
Here
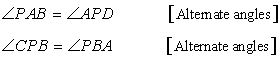
Now,
![]() …… (i)
…… (i)
Also, considering ![]() ,
,
![]() …… (ii)
…… (ii)
Therefore, from (i) and (ii)
![]()
Hence proved.
Solution 8

Steps:
1. Draw a base line AQ.
2. From A take some random distance in compass and draw one are below and above the line. Now without changing the distance in compass draw one are below and above the line. These arcs intersect each other above and below the line. Draw the line passing through these intersecting points, you will get a perpendicular to the line AQ.
3 Take distance of 4 cm in compass and mark an arc on the perpendicular above the line. Draw a line parallel to line AQ passing through through this arc.
4. From point A measure an angle of 60 degree and draw the line which intersect above drawn line at some point label it as D.
5. Using the procedure given in step 2 again draw a perpendicular to line AD.
6. Take distance of 3 cm in compass and mark an arc on the perpendicular above the line. Draw a line parallel to line AD passing through through this arc which intersect the line AQ at some point label it as B and to other line at point C.
ABCD is the required parallelogram.
Solution 9
To draw the parallelogram follows the steps:
·First draw a line AB of measure 6cm. Then draw an angle of measure ![]() at point A such that
at point A such that ![]() and AD = 5cm.
and AD = 5cm.
·Now draw a line CD parallel to the line AB of measure 6cm. Then join BC to construct the parallelogram as shown below:
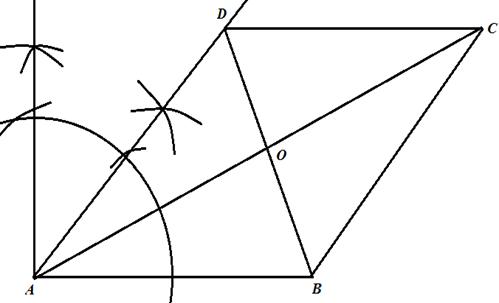
Now it is given that E is the midpoint of BC. We join OE. Now we are to prove that OE || AB and ![]() .
.
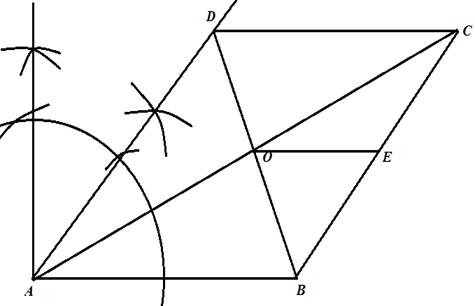
Since O is the midpoint of AC and E is the midpoint of BC, therefore the line is parallel to AB and ![]()
Solution 10
To draw the rectangle follows the steps:
(1)First draw a line AC of measure 6cm.
(2)Then draw the perpendicular bisector of AC through O.
(3)At O draw an angle of measure ![]() . Then produce OD of measure 3cm and OB of measure 3cm each.
. Then produce OD of measure 3cm and OB of measure 3cm each.
(4)Now join AD, AB, BC and CD to form the rectangle.