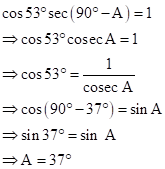Class 9 SELINA Solutions Maths Chapter 25 - Complementary Angles
Complementary Angles Exercise Ex. 25
Solution 1(a)
Correct option: (iii) 45o
sin A = cos A
Now,
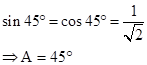
Solution 1(b)
Correct option: (iv) A + B = 90o
If sin A = cos B (A ≠ B), then A and B are complementary angles.
⇒ A + B = 90o
OR
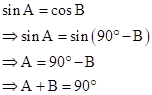
Solution 1(c)
Correct option: (i) 1
If A + B = 90o, then
cos A = sin B
cot A = tan B
![]()
Solution 1(d)
Correct option: (ii) 2
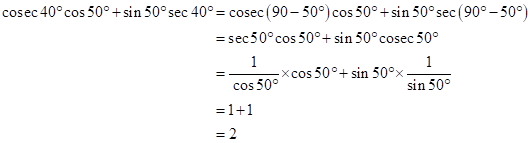
Solution 1(e)
Correct option:
(iv) ![]()
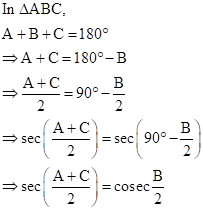
Solution 2(i)
![]()
Solution 2(ii)
![]()
Solution 2(iii)
![]()
Solution 2(iv)
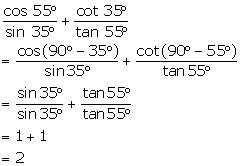
Solution 2(v)
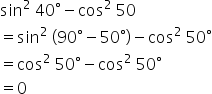
Solution 2(vi)
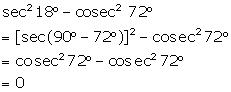
Solution 2(vii)

Solution 2(viii)

Solution 3(i)

Solution 3(ii)
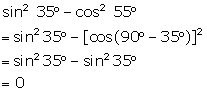
Solution 3(iii)
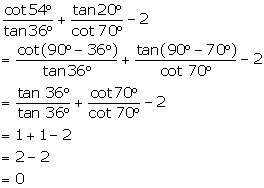
Solution 3(iv)
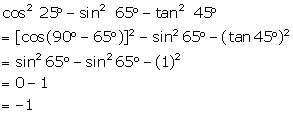
Solution 3(v)
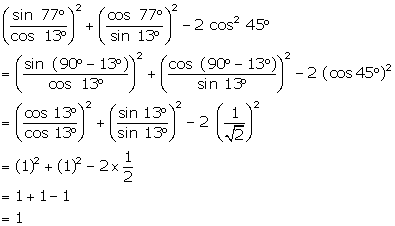
Solution 4(i)
L.H.S.
= tan 10° tan 15° tan 75° tan 80°
= tan (90° - 80°) tan (90° - 75°) tan 75° tan 80°
= cot 80° cot 75 ° tan 75° tan 80°
= (cot 80° tan 80°)(cot 75° tan 75°)
= (1)(1)
= 1
= R.H.S.
Solution 4(ii)
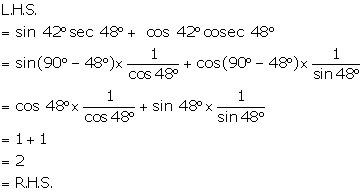
Solution 5

Solution 6
(i) We know that for a triangle ![]() ABC
ABC
![]() A +
A + ![]() B +
B + ![]() C = 180°
C = 180°
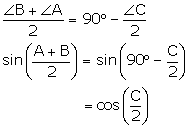
(ii) We know that for a triangle ![]() ABC
ABC
![]() A +
A + ![]() B +
B + ![]() C = 180°
C = 180°
![]() B +
B + ![]() C = 180° -
C = 180° - ![]() A
A
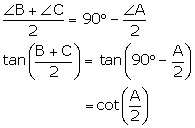
Solution 7
(i)
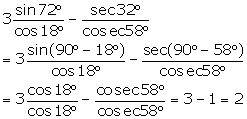

(iii) ![]()

(iv) ![]()
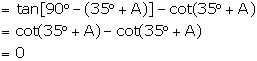
(v) ![]()
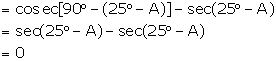
(vi) ![]()
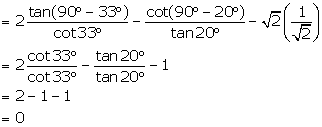
(vii) ![]()
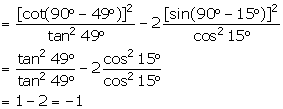
(viii) ![]()
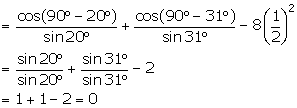
(ix) ![]()
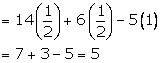
Solution 8

Solution 9(i)
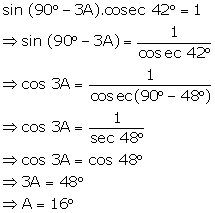
Solution 9(ii)
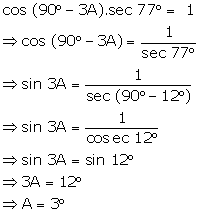
Complementary Angles Exercise Test Yourself
Solution 1
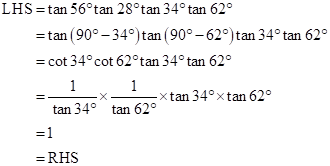
Solution 2
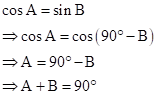
Solution 3
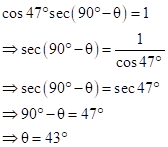
Solution 4
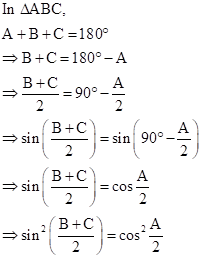
Now,
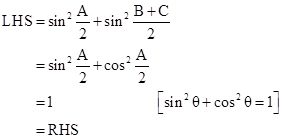
Solution 5
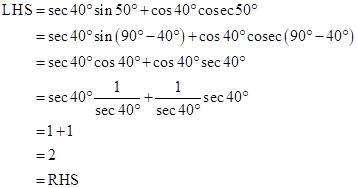
Solution 6
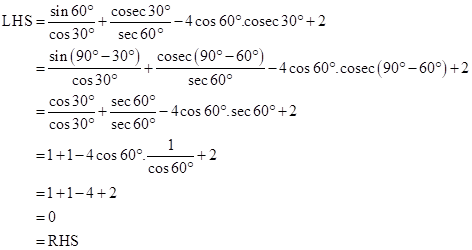
Solution 7
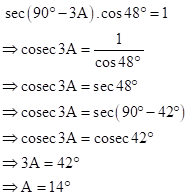
Solution 8
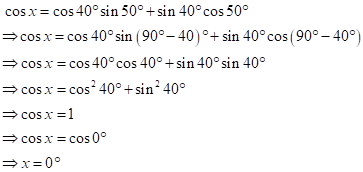
Solution 9
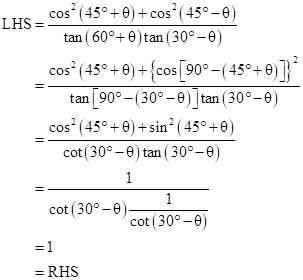
Solution 10
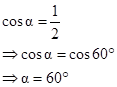
So,
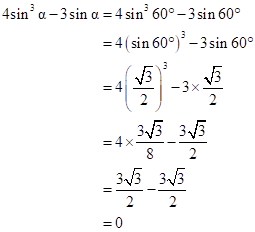
Solution 11
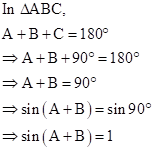
Solution 12
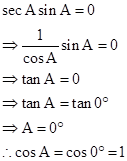
Solution 13
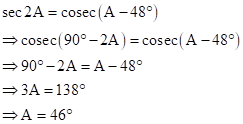
*Back answer is A = 14o. This is possible if the question is as follows:
![]()
Solution 14