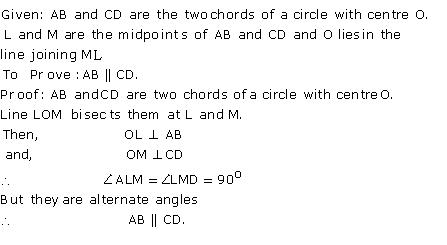Class 9 SELINA Solutions Maths Chapter 17 - Circle
Circle Exercise Ex. 17(A)
Solution 2
Let AB be the chord and O be the centre of the circle.
Let OC be the perpendicular drawn from O to AB.

We know, that the perpendicular to a chord, from the centre of a circle, bisects the chord.
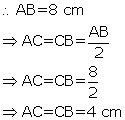
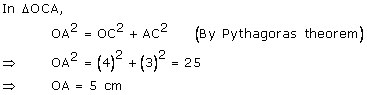
Hence, radius of the circle is 5 cm.
Solution 3
Let AB be the chord and O be the centre of the circle.
Let OC be the perpendicular drawn from O to AB.

We know, that the perpendicular to a chord, from the centre of a circle, bisects the chord.
![]() AC = CB
AC = CB
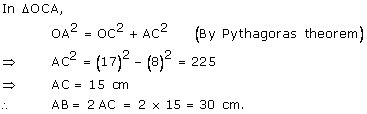
Solution 4
Let AB be the chord of length 24 cm and O be the centre of the circle.
Let OC be the perpendicular drawn from O to AB.
We know, that the perpendicular to a chord, from the centre of a circle, bisects the chord.
![]() AC = CB = 12 cm
AC = CB = 12 cm

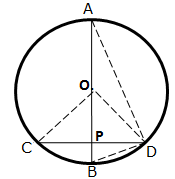
Solution 5
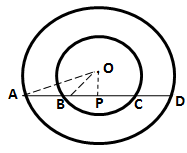
For the inner circle, BC is a chord and ![]() .
.
We know that the perpendicular to a chord, from the centre of a circle, bisects the chord.
![]() BP = PC
BP = PC

For the outer circle, AD is the chord and![]() .
.
We know that the perpendicular to a chord, from the centre of a circle, bisects the chord.
![]() AP = PD
AP = PD
By Pythagoras Theorem,
OA2 = OP2 + AP2
=> AP2 = (34)2 - (16)2 = 900
=> AP = 30 cm
AB = AP - BP = 30 - 12 = 18 cm
Solution 6
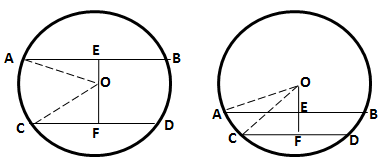
Let O be the centre of the circle and AB and CD be the two parallel chords of length 30 cm and 16 cm respectively.
Drop OE and OF perpendicular on AB and CD from the centre O.

Solution 7
Since the distance between the chords is greater than the radius of the circle (15 cm), so the chords will be on the opposite sides of the centre.
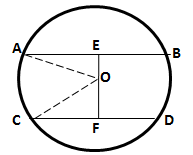
Let O be the centre of the circle and AB and CD be the two parallel chords such that AB = 24 cm.
Let length of CD be 2x cm.
Drop OE and OF perpendicular on AB and CD from the centre O.

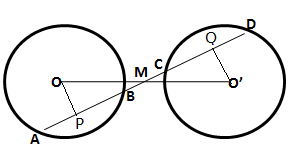
Solution 8

Solution 9

Solution 10
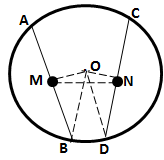

Solution 11
Drop OM and ON perpendicular on AB and CD.
Join OP, OB and OD.
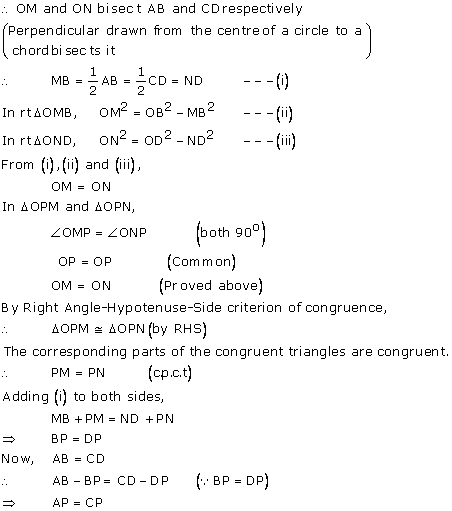
Solution 12


Solution 13
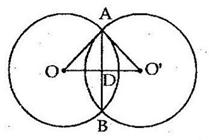

Solution 14
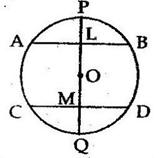
Solution 15

Solution 1(a)
Correct option: (iii) 4 cm
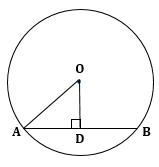
O is the centre of a circle and AB is a chord of length 6 cm.
Draw OD ⏊ chord AB.
AB = 6 cm
⇒ AD = BD = 3 cm (perpendicular to a chord from the centre of a circle bisects the chord)
Radius OA = 5 cm (Diameter = 10 cm)
In right-angled triangle ODA,
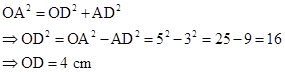
Therefore, the distance of the chord from the centre of a circle is 4 cm.
Solution 1(b)
Correct option: (i) AB = CD
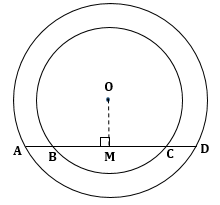
O is the centre of a circle.
Given, AD is a chord of outer circle.
And, BC is a chord of inner circle.
Draw OM ⏊ chords AD and BC.
Now, perpendicular to a chord from the centre of a circle bisects the chord.
⇒ BM = CM (I)
Also, AM = DM
⇒ AB + BM = CM + CD
⇒ AB = CD [From (I)]
Solution 1(c)
Correct option: (ii) OM < ON
Chord AB > chord CD
⇒ AB is at smaller distance from the centre as compared to chord CD.
∴ OM < ON
Solution 1(d)
Correct option: (iii) parallel to each other
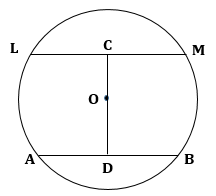
LM and AB are two chords of a circle with centre O.
C and D are mid-points of chords LM and AB respectively.
⇒ OC bisects chord LM and OD bisects chord AB.
∴ OC ⏊ LM and OD ⏊ AB.
⇒ ∠OCM = ∠ODA = 90o
But, these are alternate angles also.
⇒ LM is parallel to AB and CD is a transversal.
Therefore, if a line joining the mid-points of two chords of a circle passes through the circle, then the chords are parallel.
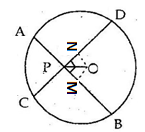
Solution 1(e)
Correct option: (iv) AB ≠ CD
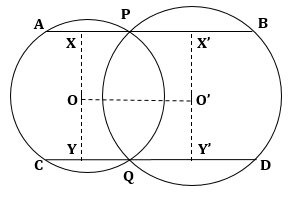
Construction:
Draw OX and OX' perpendiculars on AB.
Draw OY and OY' perpendiculars on CD.
So,
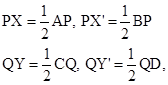
Now,
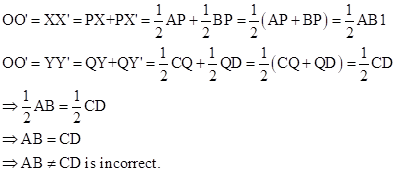
Circle Exercise Ex. 17(B)
Solution 2

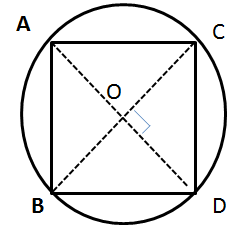

Solution 3

Solution 4
![]()
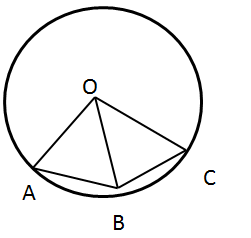

Solution 5

Solution 6

![]()
Solution 7

Solution 8

Solution 1(a)
Correct option: (i) AB = CD
In a circle, if two arcs are equal, they cut equal chords.
Therefore, if arc APB = arc CQD, then chord AB = chord CD.
Solution 1(b)
Correct option: (ii) AB < CD
∠COD > ∠AOB
⇒ arc CD > arc AB
⇒ chord CD > chord AB
That is, AB < CD
Solution 1(c)
Correct option: (ii) 3 : 2
Chord AB : chord CD = 3 : 2
⇒ arc AB : arc CD = 3 : 2
⇒ ∠AOB : ∠COD = 3 : 2
Solution 1(d)
Correct option: (iv) 120o
If an n-sided regular polygon is inscribed in a circle, then the angle subtended
by each side of this polygon at the centre of the circle ![]() .
.
Since triangle ABC is an equilateral triangle,
![]()
Solution 1(e)
Correct option: (iii) 100o
Chord AB : chord CD = 5 : 3
⇒ arc AB : arc CD = 5 : 3
⇒ ∠AOB : ∠DOC = 5 : 3

Circle Exercise Test Yourself
Solution 1
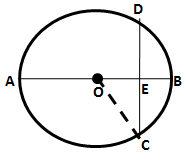
Let the radius of the circle be r cm.

Solution 2

Solution 3
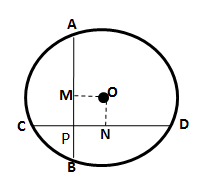
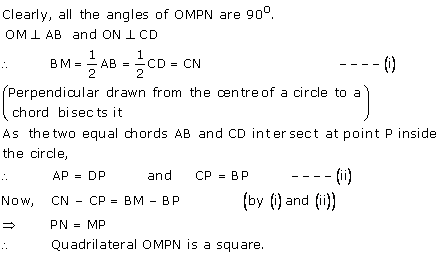
Solution 4


Solution 5
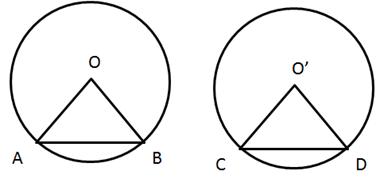

Solution 6

So, the circle can have 0, 1 or 2 points in common.
The maximum number of common points is 2.
Solution 7
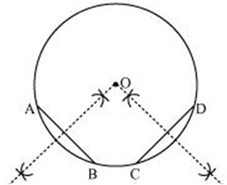

Solution 8
![]()
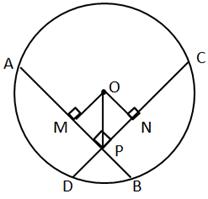

Solution 9
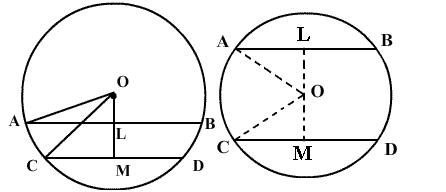

Solution 10
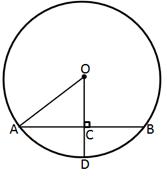

Solution 11

Solution 12

Solution 13
![]()