Class 9 SELINA Solutions Maths Chapter 16: Area Theorems [Proof and Use]
Area Theorems [Proof and Use] Exercise Ex. 16
Solution 1(a)
Correct option: (ii) 3:5
The areas of triangles with the same vertex and base along the same line are in the ratio of their bases.
ΔABD and ΔACD have the same vertex A and their bases along the same straight line BC.
Solution 1(b)
Correct option: (i) triangles of equal areas
A median of a triangle divides a triangle into two triangles of equal area.
Solution 1(c)
Correct option: (iv) BOC
Triangles ACD and BCD are on the same base CD and between the same parallels AB and CD.
So, their areas are equal.
⇒ A(ΔACD) = A(ΔBCD)
⇒ A(ΔACD) - A(ΔCOD) = A(ΔBCD) - A(ΔCOD)
⇒ A(ΔAOD) = A(ΔBOC)
Solution 1(d)
Correct option: (i) rect. CDEF
PQ is parallel to RS. FC and ED are perpendiculars to RS.
Therefore, CDEF is a rectangle.
Now, parallelogram ABEF and rectangle CDEF are on equal bases and between the same parallels.
⇒ Area of parallelogram ABEF = Area of rectangle CDEF
Solution 1(e)
Correct option: (iii) CEA
A median of a triangle divides a triangle into two triangles of equal area.
Now,
AD is the median of ΔABC.
⇒ A(ΔABD) = A(ΔACD) (I)
Also,
ED is the median of ΔEBC.
⇒ A(ΔEBD) = A(ΔECD) (II)
Subtracting (II) from (I),
A(ΔABD) - A(ΔEBD) = A(ΔACD) - A(ΔECD)
⇒ A(ΔBEA) = A(ΔCEA)
Solution 2
(i)
and parallelogram ABED are on the same base AB and between the same parallels DE//AB, so area of the triangle is half the area of parallelogram ABED.
Area of ABED = 2 (Area of ADE) = 120 cm2
(ii)Area of parallelogram is equal to the area of rectangle on the same base and of the same altitude i.e, between the same parallels
Area of ABCF = Area of ABED = 120 cm2
(iii)We know that area of triangles on the same base and between same parallel lines are equal
Area of ABE=Area of ADE =60 cm2
Solution 3
After drawing the opposite sides of AB, we get
Since from the figure, we get CD//FE therefore FC must parallel to DE. Therefore it is proved that the quadrilateral CDEF is a parallelogram.
Area of parallelogram on same base and between same parallel lines is always equal and area of parallelogram is equal to the area of rectangle on the same base and of the same altitude i.e, between same parallel lines.
So Area of CDEF= Area of ABDC + Area of ABEF
Hence Proved
Solution 4
(i)
Since POS and parallelogram PMLS are on the same base PS and between the same parallels i.e. SP//LM.
As O is the center of LM and Ratio of area of triangles with same vertex and bases along the same line is equal to ratio of their respective bases.
The area of the parallelogram is twice the area of the triangle if they lie on the same base and in between the same parallels.
So 2(Area of PSO)=Area of PMLS
Hence Proved.
(ii)
Consider the expression 
:
LM is parallel to PS and PS is parallel to RQ, therefore, LM is
Since triangle POS lie on the base PS and in between the parallels PS and LM, we have,
,
Since triangle QOR lie on the base QR and in between the parallels LM and RQ, we have,
(iii)
In a parallelogram, the diagonals bisect each other.
Therefore, OS = OQ
Consider the triangle PQS, since OS = OQ, OP is the median of the triangle PQS.
We know that median of a triangle divides it into two triangles of equal area.
Therefore,
Hence Proved.
Solution 5
(i)
Given ABCD is a parallelogram. P and Q are any points on the sides AB and BC respectively, join diagonals AC and BD.
proof:
since triangles with same base and between same set of parallel lines have equal areas
area (CPD)=area(BCD)…… (1)
again, diagonals of the parallelogram bisects area in two equal parts
area (BCD)=(1/2) area of parallelogram ABCD…… (2)
from (1) and (2)
area(CPD)=1/2 area(ABCD)…… (3)
similarly area (AQD)=area(ABD)=1/2 area(ABCD)…… (4)
from (3) and (4)
area(CPD)=area(AQD),
hence proved.
(ii)
We know that area of triangles on the same base and between same parallel lines are equal
So Area of AQD= Area of ACD= Area of PDC = Area of BDC = Area of ABC=Area of APD + Area of BPC
Hence Proved
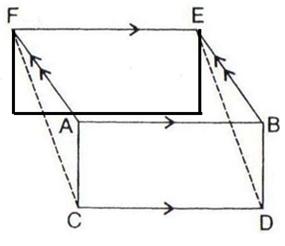
Solution 6
(i)
Since triangle BEC and parallelogram ABCD are on the same base BC and between the same parallels i.e. BC//AD.
(ii)
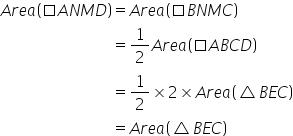
Therefore, Parallelograms ANMD and NBCM have areas equal to triangle BEC
Solution 7
Since 
DCB and DEB are on the same base DB and between the same parallels i.e. DB//CE, therefore we get
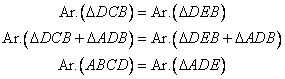
Hence proved
Solution 8
APB and parallelogram ABCD are on the same base AB and between the same parallel lines AB and CD.
ADQ and parallelogram ABCD are on the same base AD and between the same parallel lines AD and BQ.
Adding equation (i) and (ii), we get
Subtracting Ar.PCQ from both sides, we get
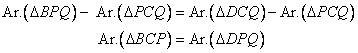
Hence proved.
Solution 9
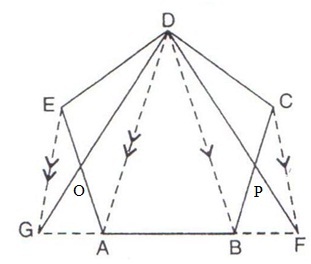
Since triangle EDG and EGA are on the same base EG and between the same parallel lines EG and DA, therefore
Subtracting 
from both sides, we have
(i)
Similarly
(ii)
Now
Hence proved
Solution 10
Joining PC we get
ABC and BPC are on the same base BC and between the same parallel lines AP and BC.
BPC and BQP are on the same base BP and between the same parallel lines BP and CQ.
From (i) and (ii), we get
Hence proved.
Solution 11
(i)
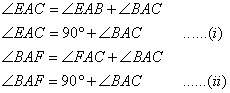
From (i) and (ii), we get
In 
EAC and BAF, we have, EA=AB
and AC=AF
EAC 
BAF (SAS axiom of congruency)
(ii)
Solution 12
(i)
In 
ABC, D is midpoint of AB and E is the midpoint of AC.
DE is parallel to BC.
Again
From the above two equations, we have
Area (ADC) = Area(AEB).
Hence Proved
(ii)
We know that area of triangles on the same base and between same parallel lines are equal
Area(triangle DBC)= Area(triangle BCE)
Area(triangle DOB) + Area(triangle BOC) = Area(triangle BOC) + Area(triangle COE)
So Area(triangle DOB) = Area(triangle COE)
Solution 13
(i) Suppose ABCD is a parallelogram (given)
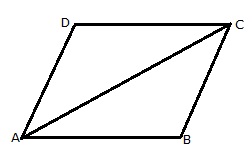
Area of congruent triangles are equal.
Therefore, Area of ABC = Area of ADC
(ii) Consider the following figure:
Here 
Since Ar.(
)=
And, Ar.(
)=
,
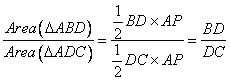hence proved
(iii) Consider the following figure:
Here
Ar.(
)=
And, Ar.()=
,
hence proved
Solution 14
AD is the median of 
ABC. Therefore it will divide ABC into two triangles of equal areas.
Area(ABD)= Area(ACD) (i)
ED is the median of EBC
Area(EBD)= Area(ECD) (ii)
Subtracting equation (ii) from (i), we obtain
Area(ABD)- Area(EBD)= Area(ACD)- Area(ECD)
Area (ABE) = Area (ACE). Hence proved
Solution 15
AD is the median of 
ABC. Therefore it will divide ABC into two triangles of equal areas.
Area(ABD)= Area(ACD)
Area (ABD)= 
Area(ABC) (i)
In ABD, E is the mid-point of AD. Therefore BE is the median.
Area(BED)= Area(ABE)
Area(ABE)= Area(ABD)
Area(ABE)= 
Area(ABC)[from equation (i)]
Area(ABE)= 
Area(ABC)
Solution 16
We have to join PD and BD.
BD is the diagonal of the parallelogram ABCD. Therefore it divides the parallelogram into two equal parts.
Area(
ABD)= Area(DBC)
=
Area (parallelogram ABCD) (i)
DP is the median of ABD. Therefore it will divide ABD into two triangles of equal areas.
Area(APD)= Area(DPB)
= Area (ABD)
= 
Area(parallelogram ABCD)[from equation (i)]
= 
Area (parallelogram ABCD) (ii)
In APD, Q is the mid-point of AD. Therefore PQ is the median.
Area(APQ)= Area(DPQ)
= Area(APD)
= 
Area (parallelogram ABCD) [from equation (ii)]
Area (APQ)= 
Area (parallelogram ABCD),hence proved
Solution 17
In 
ABC, 
BD = 
DC
Ar.(ABD):Ar.(ADC)=1:2
But Ar.(ABD)+Ar.(ADC)=Ar.(ABC)
Ar.(ABD)+2Ar.(ABD)=Ar.(ABC)
3 Ar.(ABD)= Ar.(ABC)
Ar.(ABD)= 
Ar.(ABC)
Solution 18
Ratio of area of triangles with same vertex and bases along the same line is equal to ratio of their respective bases. So, we have
_SHR_files/20140926133633_image011.gif){kind=small}
Given: Area of ΔDPB = 30 sq. cm
So area of ΔPCB = 20 sq. cm
Consider the following figure.
From the diagram, it is clear that,
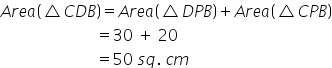
Diagonal of the parallelogram divides it into two triangles 
of equal area.
Area Theorems [Proof and Use] Exercise Test Yourself
Solution 1
(i)
Since 
EBC and parallelogram ABCD are on the same base BC and between the same parallels i.e. BC//AD.
(ii)
Parallelograms on same base and between same parallels are equal in area
Area of BCFE = Area of ABCD= 960 cm2
(iii)
Area of triangle ACD=480 = (1/2) x 30 x Altitude
Altitude=32 cm
(iv)
The area of a triangle is half that of a parallelogram on the same base and between the same parallels.
Therefore,
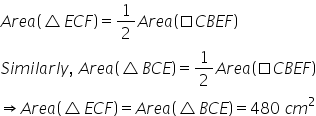
Solution 2
Here AD=DB and EC=DB, therefore EC=AD
Again, 
(opposite angles)
Since ED and CB are parallel lines and AC cut this line, therefore
From the above conditions, we have
Adding quadrilateral CBDF in both sides, we have
Area of // gm BDEC= Area of 
ABC
Solution 3
In Parallelogram PQRS, AC // PS // QR and PQ // DB // SR.
Similarly, AQRC and APSC are also parallelograms.
Since 
ABC and parallelogram AQRC are on the same base AC and between the same parallels, then
Ar.(ABC)=
Ar.(AQRC)......(i)
Similarly,
Ar.(ADC)=Ar.(APSC).......(ii)
Adding (i) and (ii), we get
Area of quadrilateral PQRS = 2 
Area of quad. ABCD
Solution 4
Given: ABCD is a trapezium
AB || CD, MN || AC
Join C and M
We know that area of triangles on the same base and between same parallel lines are equal.
So Area of Δ AMD = Area of Δ AMC
Similarly, consider AMNC quadrilateral where MN || AC.
Δ ACM and Δ ACN are on the same base and between the same parallel lines. So areas are equal.
So, Area of Δ ACM = Area of Δ CAN
From the above two equations, we can say
Area of Δ ADM = Area of Δ CAN
Hence Proved.
Solution 5
We know that area of triangles on the same base and between same parallel lines are equal.
Consider ABED quadrilateral; AD||BE
With common base, BE and between AD and BE parallel lines, we have
Area of ΔABE = Area of ΔBDE
Similarly, in BEFC quadrilateral, BE||CF
With common base BC and between BE and CF parallel lines, we have
Area of ΔBEC = Area of ΔBEF
Adding both equations, we have
Area of ΔABE + Area of ΔBEC = Area of ΔBEF + Area of ΔBDE
=> Area of AEC = Area of DBF
Hence Proved
Solution 6
Given: ABCD is a parallelogram.
We know that
Area of ΔABC = Area of ΔACD
Consider ΔABX,
Area of ΔABX = Area of ΔABC + Area of ΔACX
We also know that area of triangles on the same base and between same parallel lines are equal.
Area of ΔACX = Area of ΔCXD
From above equations, we can conclude that
Area of ΔABX = Area of ΔABC + Area of ΔACX = Area of ΔACD+ Area of ΔCXD = Area of ACXD Quadrilateral
Hence Proved
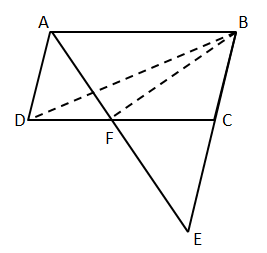
Solution 7
Join B and R and P and R.
We know that the area of the parallelogram is equal to twice the area of the triangle, if the triangle and the parallelogram are on the same base and between the parallels
Consider ABCD parallelogram:
Since the parallelogram ABCD and the triangle ABR lie on AB and between the parallels AB and DC, we have
....(1)
We know that the area of triangles with same base and between the same parallel lines are equal.
Since the triangles ABR and APR lie on the same base AR and between the parallels AR and QP, we have,
....(2)
From equations (1) and (2), we have,
Solution 8
Solution 9
Solution 10
(i)
Ratio of area of triangles with same vertex and bases along the same line is equal to the ratio of their respective bases. So, we have:
_SHR_files/20140926141021_image003.gif){kind=small}
----1
Similarly
_SHR_files/20140926141021_image005.gif){kind=small}
------2
We know that area of triangles on the same base and between same parallel lines are equal.
Area of Δ ACD = Area of Δ BCD
Area of Δ AOD + Area of Δ DOC = Area of Δ DOC + Area of Δ BOC
=> Area of Δ AOD = Area of Δ BOC ------3
From 1, 2 and 3 we have
Area (Δ DOC) = Area (Δ AOB)
Hence Proved.
(ii)
Similarly, from 1, 2 and 3, we also have
Area of Δ DCB = Area of Δ DOC + Area of Δ BOC = Area of Δ AOB + Area of Δ BOC = Area of Δ ABC
So Area of Δ DCB = Area of Δ ABC
Hence Proved.
(iii)
We know that area of triangles on the same base and between same parallel lines are equal.
Given: triangles are equal in area on the common base, so it indicates AD|| BC.
So, ABCD is a parallelogram.
Hence Proved
Solution 11
Ratio of area of triangles with the same vertex and bases along the same line is equal to the ratio of their respective bases.
So, we have
_SHR_files/20140926141021_image008.gif){kind=small}
Area of parallelogram ABCD = 324 sq.cm
Area of the triangles with the same base and between the same parallels are equal.
We know that area of the triangle is half the area of the parallelogram if they lie on the same base and between the
parallels.
Therefore, we have,
(ii)
Hence OP:OD = 1:3
Solution 12
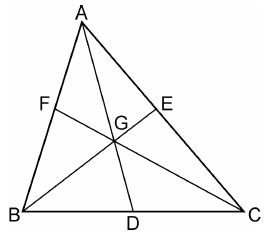
E and F are the midpoints of the sides AB and AC.
Consider the following figure.
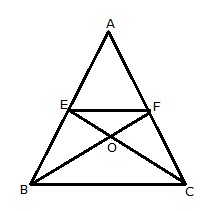
Therefore, by midpoint theorem, we have, EF || BC
Triangles BEF and CEF lie on the common base EF and between the parallels, EF and BC
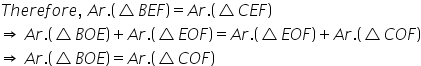
Now BF and CE are the medians of the triangle ABC
Medians of the triangle divides it into two equal areas of triangles.
Thus, we have, Ar.
ABF=Ar.CBF
Subtracting Ar.BOE on the both the sides, we have
Ar.ABF - Ar.BOE=Ar.CBF - Ar.BOE
Since, Ar.(BOE)= Ar.(COF),
Ar.ABF- Ar.BOE=Ar.CBF- Ar.COF
Ar. (quad. AEOF)=Ar.(OBC), hence proved
Solution 13
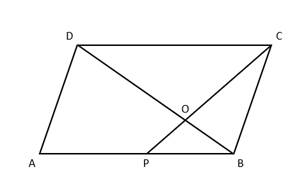
In ∆DOC and ∆BOP
∠POB = ∠DOC … (vertically opp. Angles)
Now, ▭ABCD is parallelogram,
Hence AB||DC and BD transversal
So, ∠OBP = ∠ODC … (alternate angles)
Hence,
∆DOC ~ ∆BOP …(AA test)
Hence, by area of similar triangles property
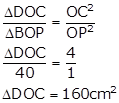
Now join DP
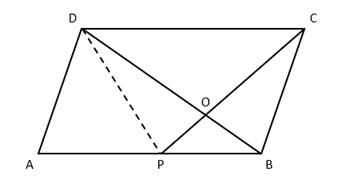
Now,
Triangles having equal base and between two same parallel lines have equal area.
Hence,
∆DPC = ΔCBD
∆DOC + ∆POD = ∆DOC + ∆BOC
Thus, ∆POD = ∆BOC …(1)
Also, we know that in a parallelogram the diagonal divides the parallelogram into two equal triangles.
Hence,
∆CBD = ∆ABD
∆DOC + ∆BOC = ∆ADP + ΔPOD + ΔPOB
From (1)
∆DOC = ∆ADP + ΔPOB
∆ADP = 160 - 40 = 120 cm2
Now, in ΔADB, AP is the median, hence
∆ADP = ∆DPB = 120
∆DPB = ΔPOD + ΔPOB
Hence ΔPOD = 120 - 40 = 80 cm2
From (1)
∆BOC = 80 cm2
ΔPBC = ΔPOB + ΔBOC = 120 cm2
Area of Parallelogram ABCD = 2ΔABD
= 2(120+40+80) = 480 cm2
ΔABC = ½ Area of Parallelogram ABCD = ½ (480) = 240 cm2
Solution 14
(i) The figure is shown below
(ii)
(iii)
Solution 15
Consider that the sides be x cm, y cm and (37-x-y) cm. also, consider that the lengths of altitudes be 6a cm, 5a cm and 4a cm.
Area of a triangle=
base
altitude
and
and
Solving both the equations, we have
X=10 cm, y=12 cm and (37-x-y)cm=15 cm
Solution 16
Solution 17
Solution 18
Solution 19
Join HF.
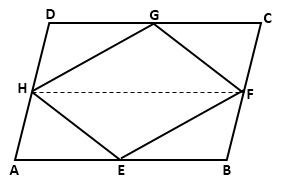
Since H and F are mid-points of AD and BC respectively,
Now, ABCD is a parallelogram.
⇒ AD = BC and AD ∥ BC
⇒ AH = BF and AH ∥ BF
⇒ ABFH is a parallelogram.
Since parallelogram FHAB and ΔFHE are on the same base FH and between the same parallels HF and AB,
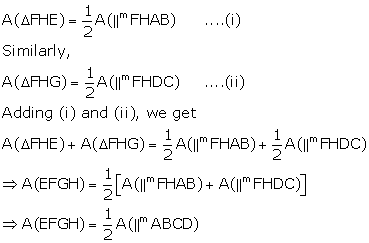
Solution 20
Join CX, DX and AY.
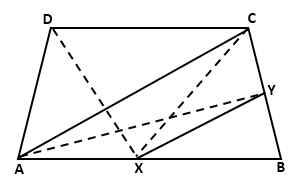
Now, triangles ADX and ACX are on the same base AX and between the parallels AB and DC.
∴ A(ΔADX) = A(ΔACX) ….(i)
Also, triangles ACX and ACY are on the same base AC and between the parallels AC and XY.
∴ A(ΔACX) = A(ΔACY) ….(ii)
From (i) and (ii), we get
A(ΔADX) = A(ΔACY)