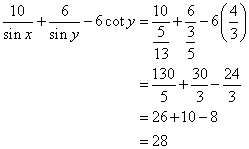Class 9 SELINA Solutions Maths Chapter 22 - Trigonometrical Ratios [Sine, Consine, Tangent of an Angle and their Reciprocals]
The ICSE syllabus emphasises both academic excellence and the holistic development of the students. The board’s curriculum is designed to build a strong foundation and provide students with critical thinking skills and practical knowledge. But to prepare for various academic and professional pursuits, students need to have more than just the textbook. Selina Solutions provides comprehensive coverage and solutions for various subjects.
One of the most important chapters in ICSE Class 9 Math is Trigonometry. Trigonometry is a branch of mathematics that teaches about the relationships between the angles and sides of right-angled triangles using trigonometric ratios, which are mathematical functions such as Sine (sin), Cosine (cos), and Tangent (tan). The reciprocals of these ratios are cosecant (cosec), secant (sec) and cotangent (cot), and they provide alternative perspectives about right-angled triangles.
Selina Class 9 Mathematics Solutions extensively covers the concepts of trigonometric ratios and their reciprocals. The resource offers clear definitions and explanations in solutions to questions posed in the Selina textbook to help students grasp trigonometry concepts and apply them in real-life situations. With step-by-step solutions and illustrative representations of triangles, it helps in geometric interpretations of trigonometric ratios.
Students can use these Solutions to solve textbook exercises, practice problems and examples to reinforce their understanding and proficiency in the chapter. Doing so helps them develop a strong foundation in trigonometry, boosts their confidence and enhances their problem-solving skills. These skills have practical applications in fields such as engineering, architecture, physics, and navigation.
At TopperLearning, Selina Solutions are designed by subject experts who have in-depth knowledge and experience in developing study materials. They thoroughly understand the ICSE curriculum and keep up-to-date with the latest syllabus.
With access to neatly designed textbook solutions, students can find and refer to any topic with just a few clicks. TopperLearning also brings forth video lessons, multiple choice questions and sample tests that not only help them understand the concept better and clear their doubts but they save time which they can use for revision. Thus, TopperLearning helps improve learning outcomes and creates toppers!
Trigonometrical Ratios [Sine, Consine, Tangent of an Angle and their Reciprocals] Exercise Ex. 22(A)
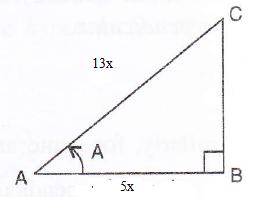
Solution 1(a)
Correct option: (i) ![]()
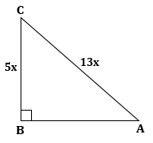
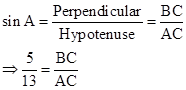
∴ If length of BC = 5x, length of AC = 13x
Now,

Solution 1(b)
Correct option: (ii) 1
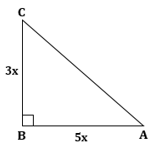
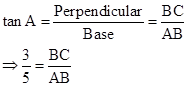
∴ If length of BC = 3x, length of AB = 5x
Now,

So,
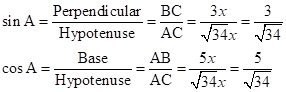
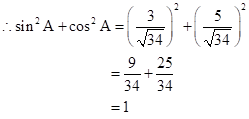
Solution 1(c)
Correct option: (iv) -1

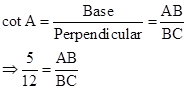
∴ If length of AB = 5x, length of BC = 12x
Now,
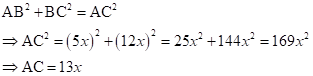
So,
![]()
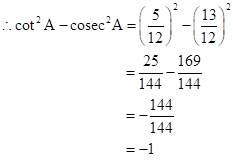
Solution 1(d)
Correct option: (iii)
![]()
In right-angled ΔADB,
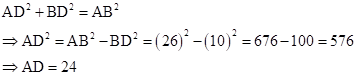
Now,
![]()
Solution 1(e)
Correct option: (i) 1

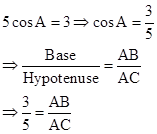
∴ If length of AB = 3x, length of AC = 5x
Now,
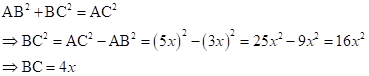
So,
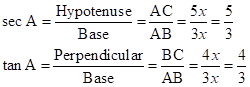
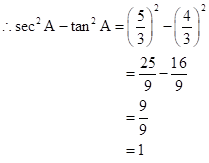
Solution 2
Given angle ![]()
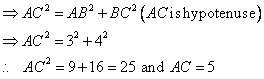
(i)
![]()
(ii)
![]()
(iii)
![]()
(iv)
![]()
(v)
![]()
(vi)
![]()
Solution 3
Given angle ![]()
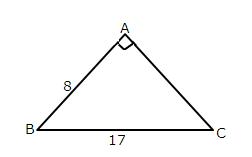

(i)
![]()
(ii)
![]()
(iii)
![]()
![]()
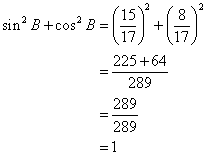
(iv)
![]()
![]()
![]()
![]()
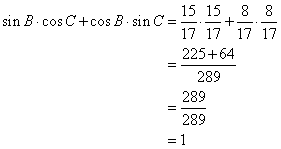
Solution 4
Consider the diagram as

Given angle ![]() and
and ![]()


(i)
![]()
(ii)
![]()
(iii)
![]()
![]()
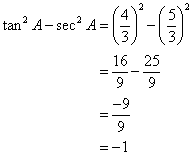
(iv)
![]()
(v)
![]()
(vi)
![]()
![]()

Solution 5
Given angle ![]() and
and ![]()



(i)
![]()
(ii)
![]()
(iii)
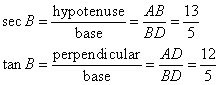
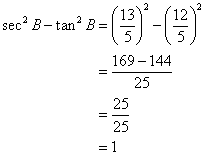
(iv)


Solution 6
Consider the diagram below:
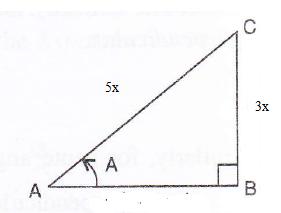
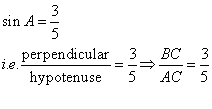
Therefore if length of ![]() , length of
, length of ![]()
Since

Now
(i)
![]()
(ii)
![]()
Solution 7
Given angle ![]() in the figure
in the figure

Now
(i)![]()
(ii)![]()
(iii)![]()
![]()
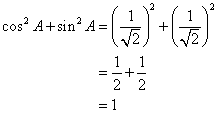
Solution 8
Consider the diagram below:
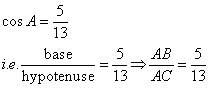
Therefore if length of ![]() , length of
, length of ![]()
Since

Now
![]()
![]()
![]()
(i)
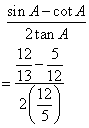

(ii)
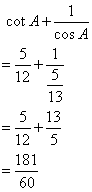
Solution 9
Consider the diagram below:
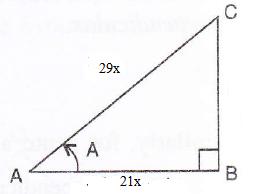
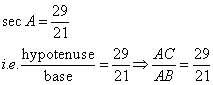
Therefore if length of ![]() , length of
, length of ![]()
Since

Now
![]()
![]()
Therefore

Solution 10
Consider the diagram below:
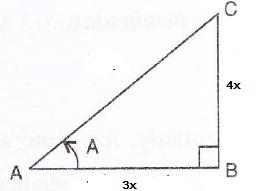
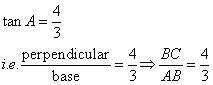
Therefore if length of ![]() , length of
, length of ![]()
Since

Now
![]()
![]()
![]()
Therefore
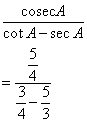
![]()
![]()
Solution 11
Consider the diagram below:
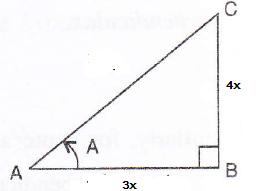
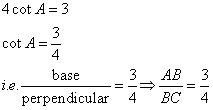
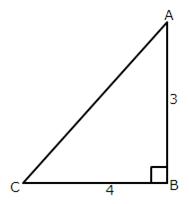
Therefore if length of AB = 3x, length of BC = 4x
Since

(i)
![]()
(ii)
![]()
(iii)
![]()
![]()
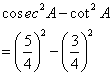
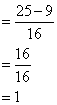
Solution 12
Consider the diagram below:
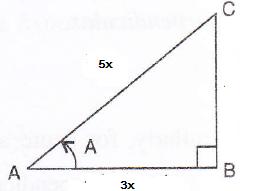
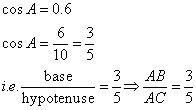
Therefore if length of AB = 3x, length of AC = 5x
Since

Now all other trigonometric ratios are
![]()
![]()
![]()
![]()
![]()
Solution 13
Consider the diagram below:
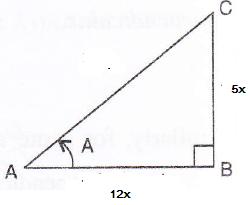
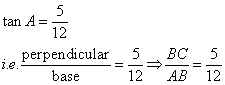
Therefore if length of AB = 12x, length of BC = 5x
Since

(i)
![]()
(ii)
![]()
(iii)
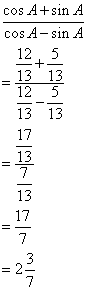
Solution 14
Consider the diagram below:

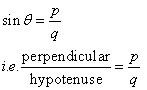
Therefore if length of perpendicular = px, length of hypotenuse = qx
Since

Now
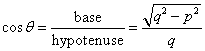
Therefore
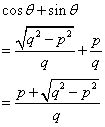
Solution 15
Consider the diagram below:
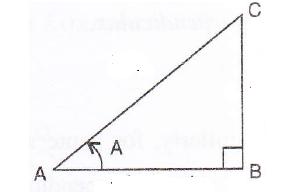
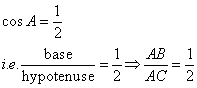
Therefore if length of AB = x, length of AC = 2x
Since

Consider the diagram below:
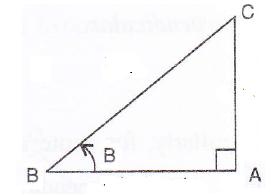
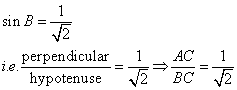
Therefore if length of AC = x, length of ![]()
Since

Now
![]()
![]()
Therefore
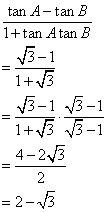
Trigonometrical Ratios [Sine, Consine, Tangent of an Angle and their Reciprocals] Exercise Ex. 22(B)
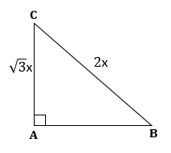
Solution 1(a)
Correct option: (i) ![]()
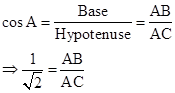
∴ If length of AB =
x, length of AC = ![]() x
x
Now,
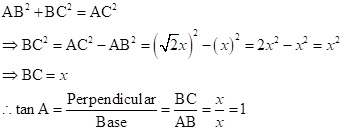
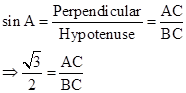
∴ If length of AC =
![]() x, length of BC = 2x
x, length of BC = 2x
Now,
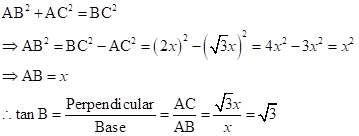
![]()
Solution 1(b)
Correct option: (iii)
![]()
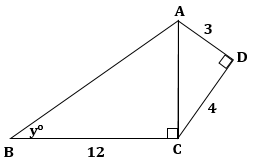
In right-angled ΔADC,
![]()
In right-angled ΔACB,
![]()
Now,
![]()
Solution 1(c)
Correct option: (i) ![]()

Let the diagonals BD and AC of a rhombus intersect each other at O.
Given, BD = 12 cm, AC = 16 cm.
Diagonals of a rhombus bisect each other at right angles.
⇒ OB = OD = 6 cm, OA = OC = 8 cm and ∠AOB = 90o
In right-angled ΔAOB,
![]()
Now,
![]()
Solution 1(d)
Correct option: (iv) 6
In right-angled ΔADB,
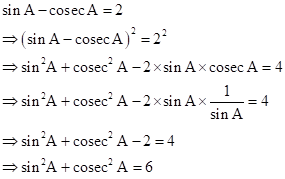
Solution 1(e)
Correct option: (ii)
![]()
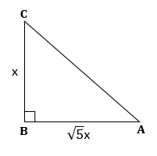
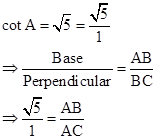
∴ If length of AB =
![]() x, length of BC = x
x, length of BC = x
Now,
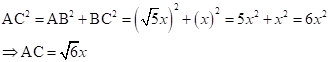
So,
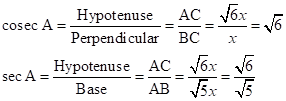
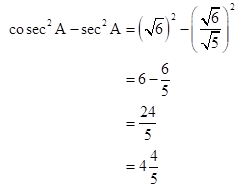
Solution 2
Consider the given figure
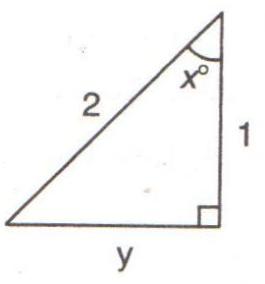
(i)
Since the triangle is a right angled triangle, so using Pythagorean Theorem
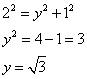
(ii)
![]()
(iii)
![]()
![]()
Therefore
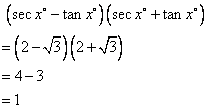
Solution 3
Consider the given figure
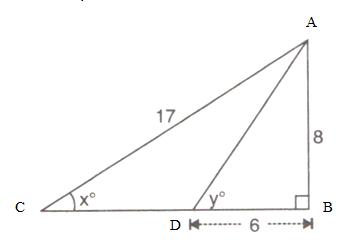
Since the triangle is a right angled triangle, so using Pythagorean Theorem
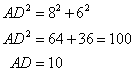
Also
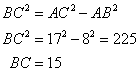
(i)
![]()
(ii)
![]()
(iii)
![]()
![]()
![]()
Therefore
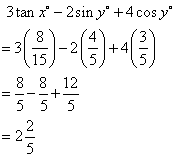
Solution 4
Consider the given figure
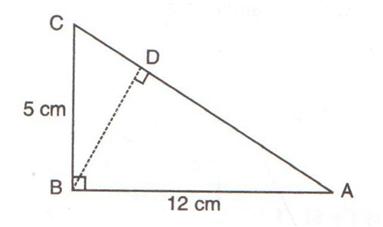
Since the triangle is a right angled triangle, so using Pythagorean Theorem

In ![]() and
and ![]() , the
, the ![]() is common to both the triangles,
is common to both the triangles, ![]() so therefore
so therefore![]() .
.
Therefore ![]() and
and ![]() are similar triangles according to AAA Rule
are similar triangles according to AAA Rule
So

(i)
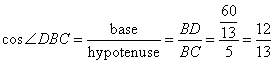
(ii)
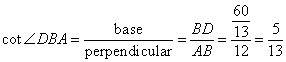
Solution 5
Consider the given figure
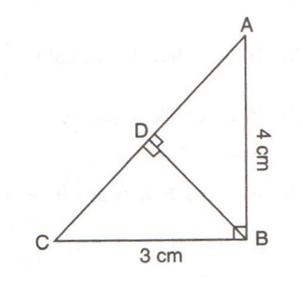
Since the triangle is a right angled triangle, so using Pythagorean Theorem
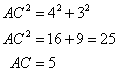
In ![]() and
and ![]() , the
, the ![]() is common to both the triangles,
is common to both the triangles, ![]() so therefore
so therefore![]() .
.
Therefore ![]() and
and ![]() are similar triangles according to AAA Rule
are similar triangles according to AAA Rule
So
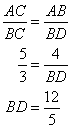
Now using Pythagorean Theorem
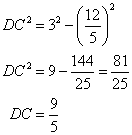
Therefore

(i)
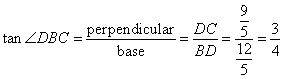
(ii)
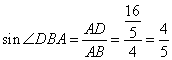
Solution 6
Consider the figure below
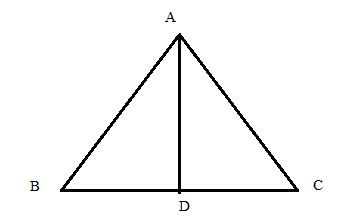
In the isosceles ![]() ,
, ![]() and
and ![]() the perpendicular drawn from angle
the perpendicular drawn from angle ![]() to the side
to the side ![]() divides the side
divides the side ![]() into two equal parts
into two equal parts ![]()
![]()
Solution 7
Consider the figure below
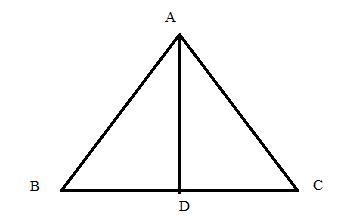
In the isosceles ![]() ,
, ![]() and
and ![]() the perpendicular drawn from angle
the perpendicular drawn from angle ![]() to the side
to the side ![]() divides the side
divides the side ![]() into two equal parts
into two equal parts ![]()
Since ![]()

(i)
![]()
(ii)
![]()
(iii)
![]()
![]()
Therefore

(iv)
![]()
![]()
Therefore
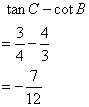
Solution 8
Consider the figure
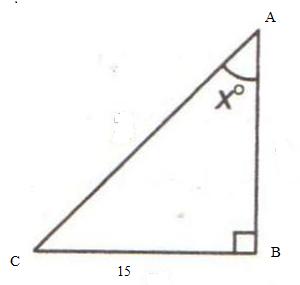

Therefore if length of base = 4x, length of perpendicular = 3x
Since
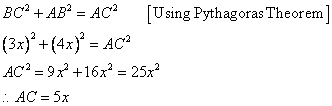
Now
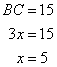
Therefore
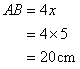
And
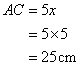
Solution 9
Consider the figure
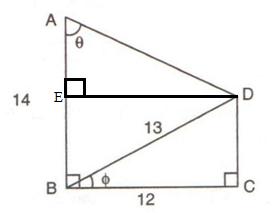
A perpendicular is drawn from D to the side AB at point E which makes BCDE is a rectangle.
Now in right angled triangle BCD using Pythagorean Theorem

Since BCDE is rectangle so ED 12 cm, EB = 5 and AE = 14 - 5 = 9
(i)
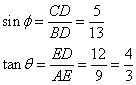
(ii)
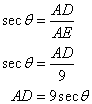
Or
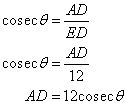
Solution 10
Given
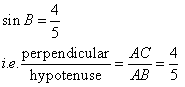
Therefore if length of perpendicular = 4x, length of hypotenuse = 5x
Since
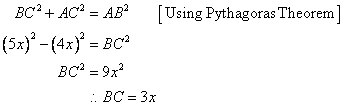
Now
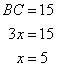
(i)
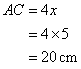
And
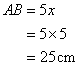
(ii)
Given
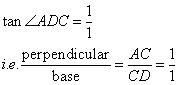
Therefore if length of perpendicular = x, length of hypotenuse = x
Since

Now
![]()
So
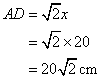
And
![]()
Now
![]()
![]()
So
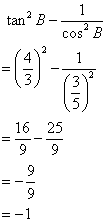
Solution 11
![]()
Squaring both sides

Solution 12
![]()
Squaring both sides

Solution 13
Consider the diagram below:
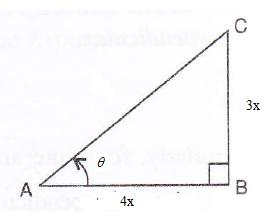

Therefore if length of BC = 3x, length of AB = 4x
Since

(i)
![]()
(ii)
![]()
(iii)
![]()
![]()
Therefore

(iv)
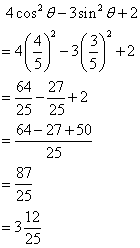
Solution 14
Consider the diagram below:
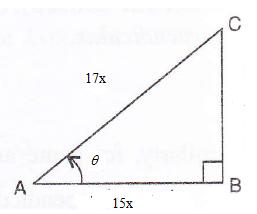
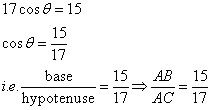
Therefore if length of AB = 15x, length of AC = 17x
Since

Now
![]()
![]()
Therefore
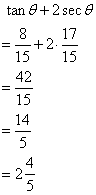
Solution 15
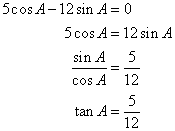
Now
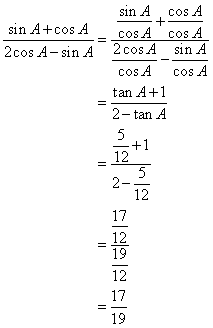
Trigonometrical Ratios [Sine, Consine, Tangent of an Angle and their Reciprocals] Exercise Test Yourself
Solution 1
Consider the diagram below:
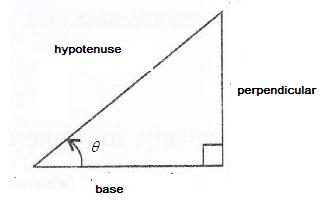
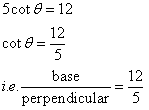
Therefore if length of base = 12x, length of perpendicular = 5x
Since

Now
![]()
![]()
Therefore
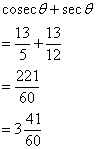
Solution 2
Consider the diagram below:
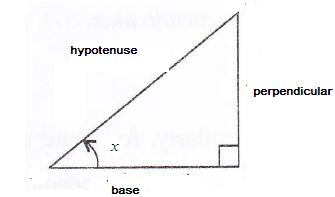

Therefore if length of base = 3x, length of perpendicular = 4x
Since
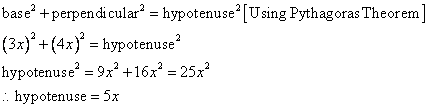
Now
![]()
![]()
Therefore
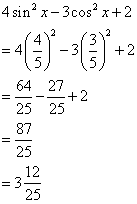
Solution 3
Consider the diagram below:
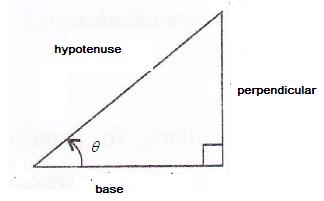
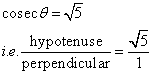
Therefore if length of hypotenuse ![]() , length of perpendicular = x
, length of perpendicular = x
Since

Now
![]()
![]()
(i)

(ii)
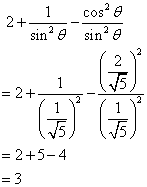
Solution 4
Consider the diagram below:
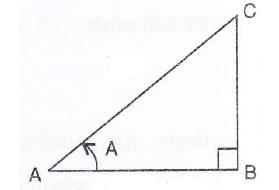
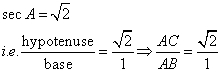
Therefore if length of AB = x, length of ![]()
Since

Now
![]()
![]()
![]()
Therefore

Solution 5
Consider the diagram below:
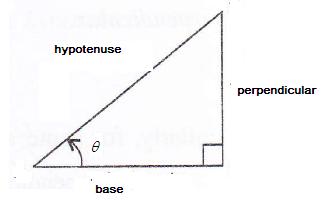
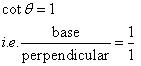
Therefore if length of base = x, length of perpendicular = x
Since
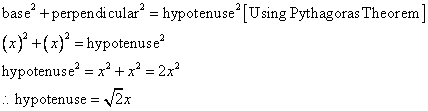
Now
![]()
![]()
Therefore

Solution 6
Given angle ![]() and
and ![]() in the figure
in the figure
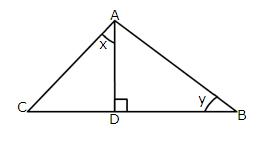

Again

Now
(i)
![]()
(ii)
![]()
![]()
Therefore
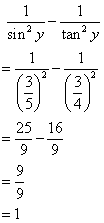
(iii)
![]()
![]()
![]()
Therefore
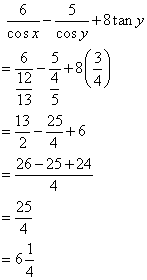
Solution 7
Since ![]() is mid-point of
is mid-point of ![]() so
so ![]()
(i)
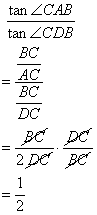
(ii)
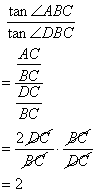
Solution 8
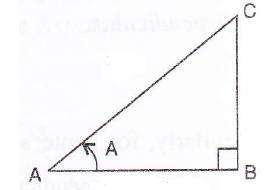
Consider the diagram below:
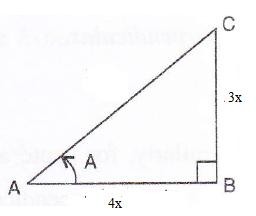
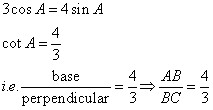
Therefore if length of AB = 4x, length of BC = 3x
Since

(i)
![]()
(ii)
![]()
Therefore
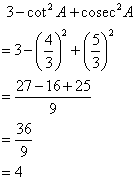
Solution 9
Consider the figure
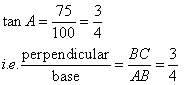
Therefore if length of base = 4x, length of perpendicular = 3x
Since
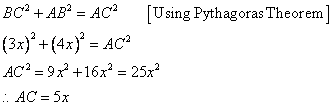
Now
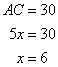
Therefore
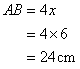
And
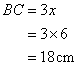
Solution 10
Consider the figure
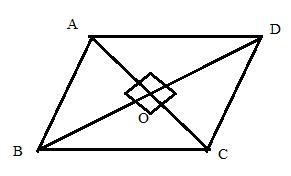
The diagonals of a rhombus bisects each other perpendicularly
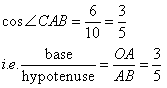
Therefore if length of base = 3x, length of hypotenuse = 5x
Since

Now
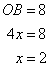
Therefore
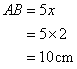
And
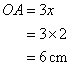
Since the sides of a rhombus are equal so the length of the side of the rhombus ![]()
The diagonals are
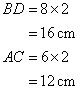
Solution 11
Consider the figure below
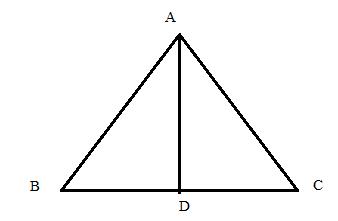
In the isosceles ![]() , the perpendicular drawn from angle
, the perpendicular drawn from angle ![]() to the side
to the side ![]() divides the side
divides the side ![]() into two equal parts
into two equal parts ![]()
Since ![]()

(i)
![]()
(ii)
![]()
(iii)
![]()
![]()
Therefore
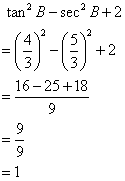
Solution 12
Consider the figure below

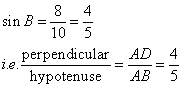
Therefore if length of perpendicular = 4x, length of hypotenuse = 5x
Since

Now
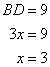
Therefore

And
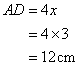
Again
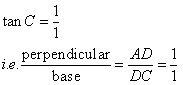
Therefore if length of perpendicular = x, length of base = x
Since

Now
![]()
Therefore
![]()
And
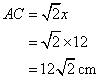
Solution 13
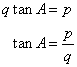
Now

Solution 14
Consider the figure

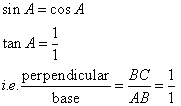
Therefore if length of perpendicular = x, length of base = x
Since

Now
![]()
Therefore

Solution 15
Consider the diagram
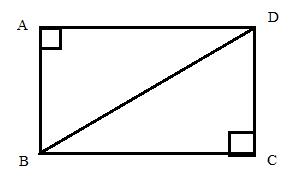
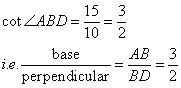
Therefore if length of base = 3x, length of perpendicular = 2x
Since

Now
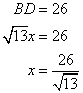
Therefore
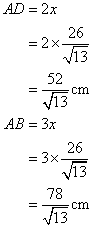
Now
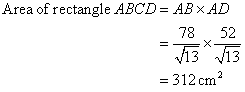

Solution 16
Consider the figure
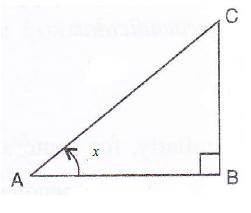
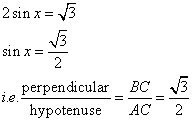
Therefore if length of ![]() , length of
, length of ![]()
Since

Now
![]()
(i)
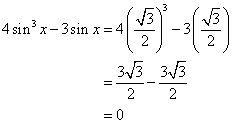
(ii)

Solution 17
Consider the diagram below:
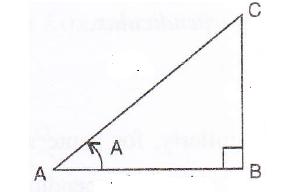

Therefore if length of ![]() , length of
, length of ![]()
Since
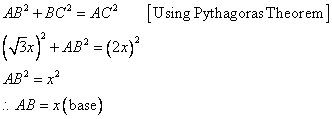
Consider the diagram below:
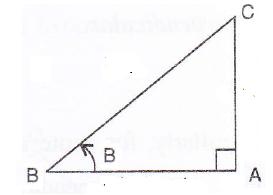
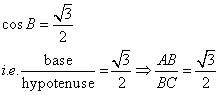
Therefore if length of ![]() , length of
, length of ![]()
Since

Now
![]()
![]()
Therefore
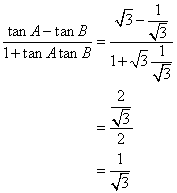
Solution 18
Consider the figure
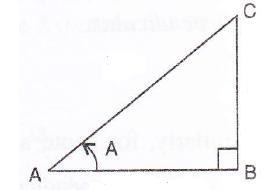
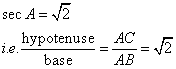
Therefore if length of ![]() , length of
, length of ![]()
Since

Now
![]()
![]()
![]()
![]()
Therefore

Solution 19
![]()
Now

Solution 20
![]()
Squaring both sides

Solution 21
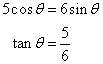
Now
(i)
![]()
(ii)
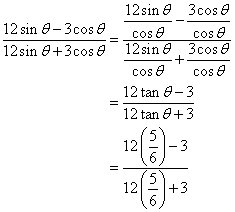
![]()
Solution 22
Consider the given diagram as
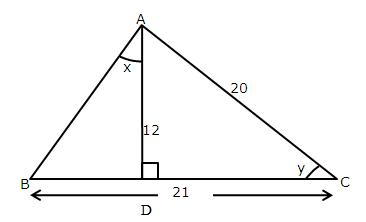
Using Pythagorean Theorem
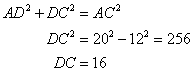
Now
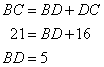
Again using Pythagorean Theorem
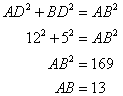
Now
![]()
![]()
![]()
Therefore