Class 9 SELINA Solutions Maths Chapter 6 - Simultaneous (Linear) Equations (Including Problems)
Simultaneous (Linear) Equations (Including Problems) Exercise Ex. 6(A)
Solution 1(a)
Correct
option: (iii) ![]()
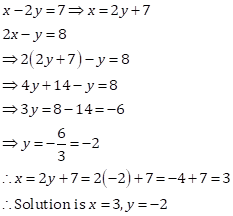
Solution 1(b)
Correct
option: (i) ![]()
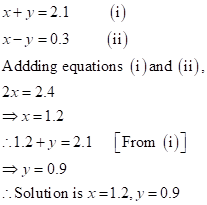
Solution 1(c)
Correct option:
(iv) ![]()
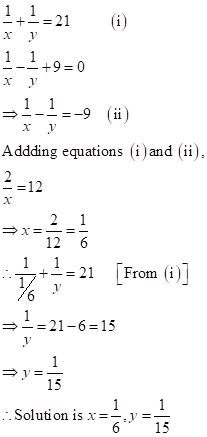
Solution 1(d)
Correct
option: (ii) ![]()
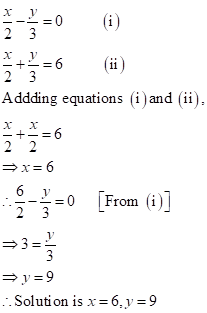
Solution 1(e)
Correct
option: (i) ![]()
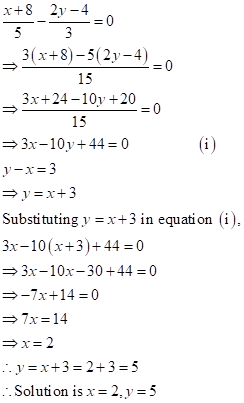
Solution 2
8x + 5y = 9...(1)
3x + 2y = 4...(2)
(2)![]() y =
y = ![]()
Putting this value of y in (2)
3x + 2 ![]()
15x + 18 - 16x = 20
x = -2
From (1) y = ![]() =
= ![]()
y = 5
Solution 3
2x - 3y = 7...(1)
5x + y = 9...(2)
(2)![]() y = 9 - 5x
y = 9 - 5x
Putting this value of y in (1)
2x - 3 (9 - 5x) = 7
2x - 27 + 15x = 7
17x = 34
x = 2
From (2)
y = 9 - 5(2)
y = -1
Solution 4
2x + 3y = 8...(1)
2x = 2 + 3y...(2)
(2) ![]() 2x = 2 + 3y
2x = 2 + 3y
Putting this value of 2x in (1)
2 + 3y + 3y = 8
6y = 6
y = 1
From (2) 2x = 2 + 3 (1)
x = ![]()
x = 2.5
Solution 5
_files/20140922172633_image002.gif)
Solution 6
6x = 7y + 7...(1)
7y - x = 8...(2)
(2) ![]() x = 7y - 8
x = 7y - 8
Putting this value of x in (1)
6(7y - 8) = 7y + 7
42y - 48 = 7y + 7
35y = 55
![]()
From (2) x = ![]()
x = 3
Solution 7
y = 4x -7...(1)
16x- 5y = 25...(2)
(1) ![]() y = 4x - 7
y = 4x - 7
Putting this value of y in (2)
16x - 5 (4x - 7) = 25
16x - 20x + 35 = 25
-4x = -10
![]()
From (1)
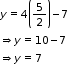
y = 10-7=3
Solution is ![]() .
.
Solution 8
2x + 7y = 39...(1)
3x + 5y = 31...(2)
(1) ![]() x =
x = ![]()
Putting this value of x in (2)
![]()
117 - 21y + 10y = 62
-11y = -55
y = 5
From (1) x = ![]()
![]()
Solution 9
_files/20140922172633_image004.gif)
Solution 10
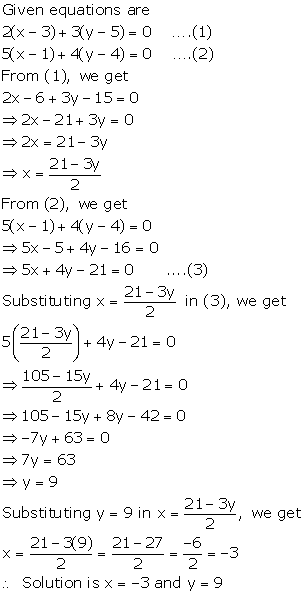
Solution 11
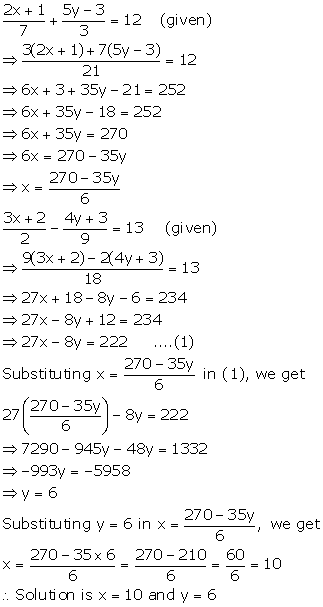
Solution 12
13 + 2y = 9x...(1)
3y = 7x...(2)
Multiplying equation no. (1) by 3 and (2) by 2, we get,
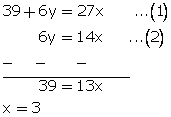
From (2)
3y = 7(3)
y = 7
Solution 13
3x - y = 23...(1)
![]()
4x + 3y = 48...(2)
Multiplying equation no. (1) by 3
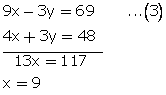
From (1)
3(9) - y = 23
y = 27 - 23
y = 4
Solution 14
_files/20140922185444_image004.gif)
Solution 15
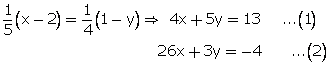
Multiplying equation no. (1) by 3 and(2) by 5.

From (1)
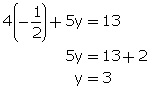
Solution 16
y = 2x - 6
y = 0
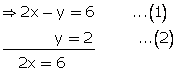
x = 3 ; y = 0
Solution 17
_files/20140922185444_image008.gif)
Solution 18
3 - (x - 5) = y + 2
2(x + y) = 4 - 3y
![]() -x - y = -6
-x - y = -6
![]() x + y = 6...(1)
x + y = 6...(1)
2x + 5y = 4...(2)
Multiplying equation no. (1) by 2.
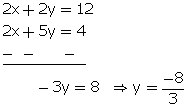
From (1)
![]()
Solution 19
2x -3y - 3 = 0
![]()
![]() 2x - 3y = 3...(1)
2x - 3y = 3...(1)
![]() 4x + 24y = -3...(2)
4x + 24y = -3...(2)
Multiplying equation no. (1) by 8.
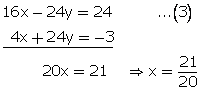
From (1)
![]()
![]()
Solution 20
13x + 11y = 70...(1)
11x+ 13y = 74...(2)
Adding(1) and (2)
24x + 24y = 144
x + y = 6...(3)
subtracting (2) from (1)
2x - 2y = -4
x - y = -2...(4)
x + y = 6...(3)
![]()
From (3)![]()
2 + y = 6![]() y = 4
y = 4
Solution 21
41x + 53y = 135...(1)
53x + 41y = 147...(2)
Adding (1) and (2)
94x + 94y = 282
x + y = 3...(3)
Subtracting (2) from (1)
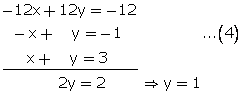
From (3)
x + 1 = 3![]() x = 2
x = 2
Solution 22
2x + y = 23...(1)
4x - y = 19...(2)
Adding equation (1) and (2) we get,
2x + y = 23
4x - y = 19
![]()
From (1)
2(7) + y = 23
y = 23 - 14
![]() y = 9
y = 9
![]() x - 3y = 7 - 3(9) = -20
x - 3y = 7 - 3(9) = -20
And 5y - 2x = 5(9) - 2(7) = 45- 14 = 31
Solution 23
10 y = 7x - 4
-7x + 10y = -4...(1)
12x + 18y = 1...(2)
Multiplying equation no. (1) by 12 and (2) by 7.
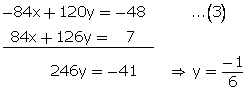
From (1)
-7x + 10 ![]()
-7x = -4 + ![]()
![]()
![]() 4
4![]() and 8y - x = 8
and 8y - x = 8 ![]()
Solution 24
(i)
_files/20140922185444_image012.gif)
(ii)
_files/20140922185444_image014.gif)
Simultaneous (Linear) Equations (Including Problems) Exercise Ex. 6(B)
Solution 1(a)
Correct
option: (ii) ![]()
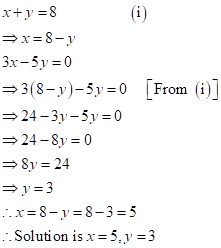
Solution 1(b)
Correct
option: (iii) ![]()
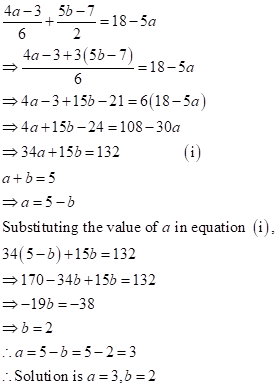
Solution 1(c)
Correct
option: (iv) ![]()
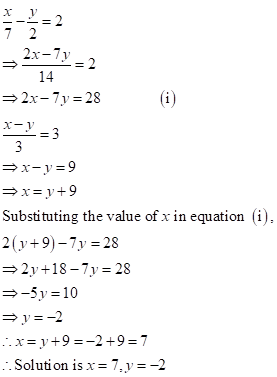
Solution 1(d)
Correct
option: (ii) ![]()
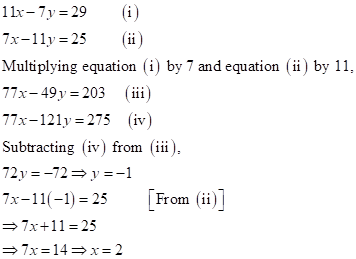
![]()
Solution 1(e)
Correct
option: (iii) ![]()
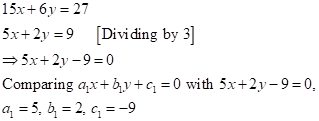
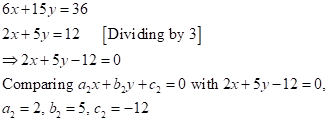
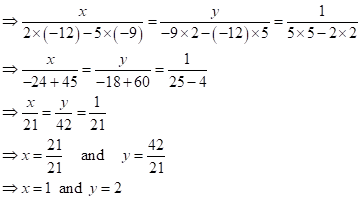
Solution 1(f)
Correct option:
(iii) ![]()
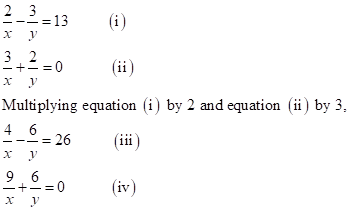
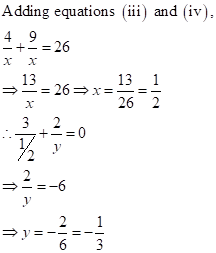
Solution 2
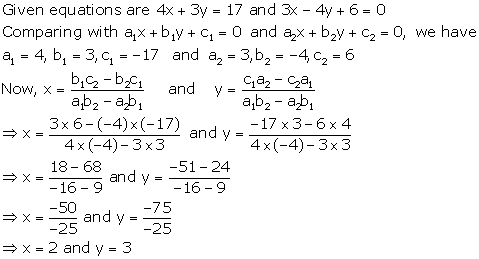
Solution 3
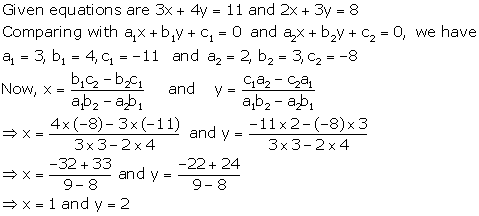
Solution 4
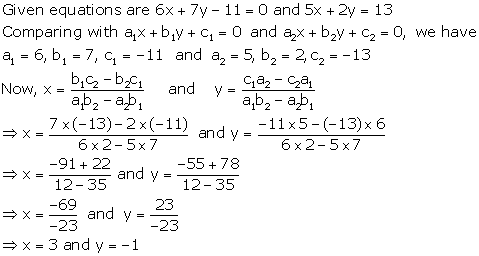
Solution 5
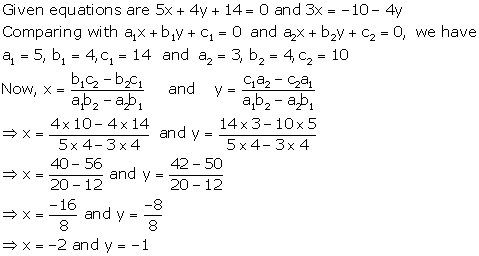
Solution 6
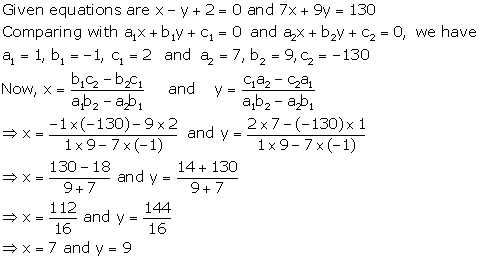
Solution 7
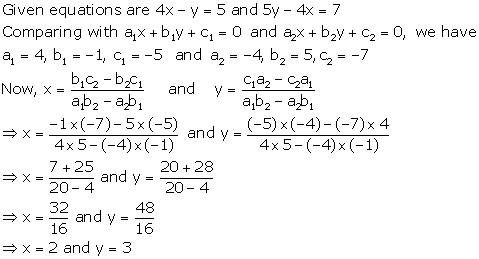
Solution 8
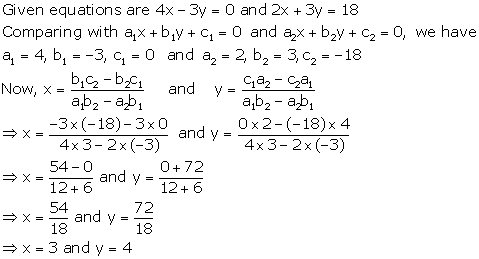
Solution 9
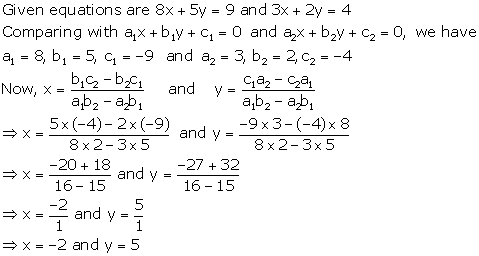
Solution 10
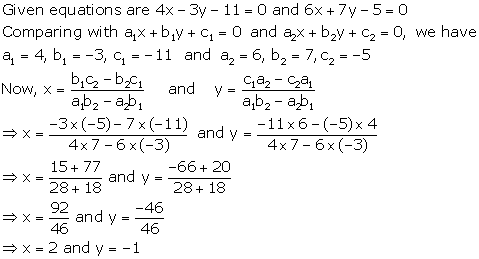
Solution 11
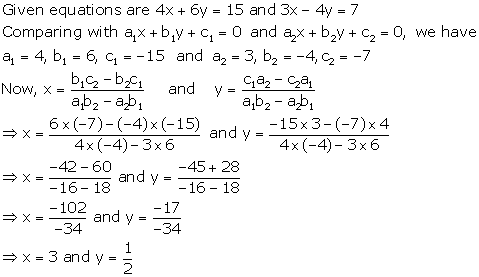
Solution 12
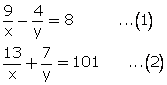
Multiplying equation no. (1) by 7 and (2) by 4.

From (1)
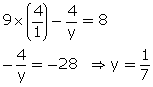
Solution 13
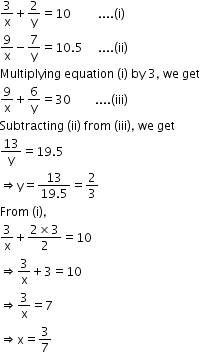
Solution 14
Solve
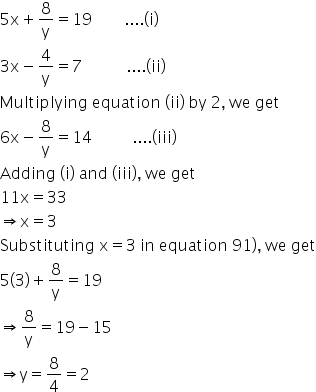
Solution 15

Solution 16
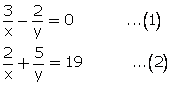
Multiplying equation no. (1) by 5 and (2) by 2.
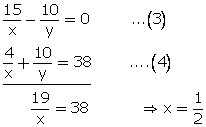
From (1) 3![]()
![]() y = ax + 3
y = ax + 3
![]()
![]()
Solution 17
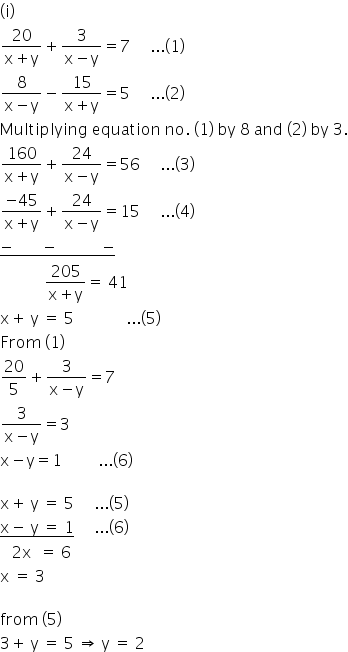
(ii)

Solution 18
(i)

From (1)
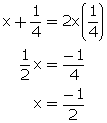
(ii)
x + y = 7xy...(1)
2x - 3 = -xy...(2)
Multiplying equation no. (1) by 3.
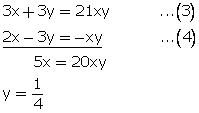
From (1)
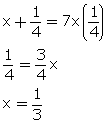
Solution 19

Solution 20
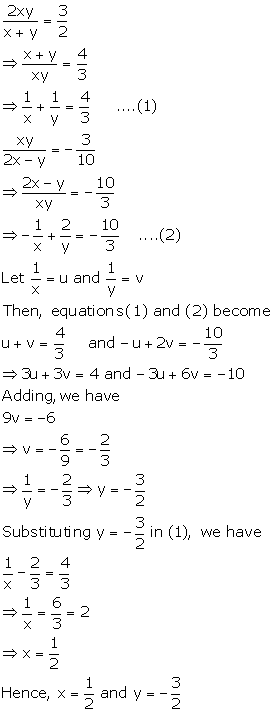
Simultaneous (Linear) Equations (Including Problems) Exercise Ex. 6(C)
Solution 1(a)
Correct option: (i) 12 and 3
Let the
two positive whole numbers be ![]() and
and ![]() .
.
Then,
![]()
Adding equations (i) and (ii),
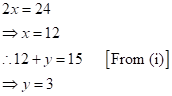
Therefore, the two positive whole numbers are 12 and 3.
Solution 1(b)
Correct option:
(ii) ![]()
Let the fraction be
![]() .
.
Then,
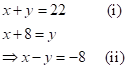
Adding equations (i) and (ii),
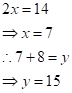
Therefore, the
fraction is ![]() .
.
Solution 1(c)
Correct option: (iv) 62
Let ![]() be the digit at
ten's place and
be the digit at
ten's place and ![]() be the digit at unit's place.
be the digit at unit's place.
∴ The number is ![]() .
.
Then,
![]()
Adding equations (i) and (ii),
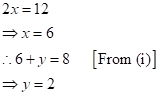
Therefore, a two-digit number is 62.
Solution 1(d)
Correct option: (ii) 15 years and 45 years
Let the
present ages of two persons be ![]() years and
years and ![]() years respectively.
years respectively.
Then,
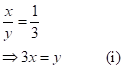
After 5 years,
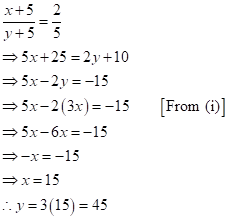
Therefore, their ages are 15 years and 45 years respectively.
Solution 2
Let the two numbers be x and y
According to the question,
![]()
3x - 2y = 0...(1)
Also,![]()
2x - 3y = -20...(2)
Multiplying equation no. (1) by 2 and (2) by 3and substracting
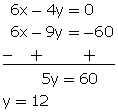
From (1), we get
3x - 2(12) = 0
![]()
x = 8
Thus, the numbers are 8 and 12.
Solution 3
Let the smaller number be x
and the larger number be y.
According to the question,
![]()
7x -; 4y = 0...(1)
and,3y + 2x = 59...(2)
Multiplying equation no. (1) by 3 and (2) by 4.and adding them
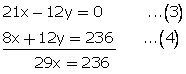
x = ![]()
From (1)
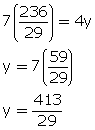
Hence, the number are ![]()
Solution 4
Let the two numbers be a and b respectively such that b > a.
According to given condition,

Solution 5
Two numbers are x and y such that x > y.
Now,
x + y = 50 ….(i)
And,
y2 - x2 = 720
⇒ (y - x)(y + x) = 720
⇒ (y - x)(50) = 720
⇒ y - x = 14.4 ….(ii)
Adding (i) and (ii), we get
2y = 64.4
⇒ y = 32.2
Substituting the value of y in (i), we have
x + 32.2 = 50
⇒ x = 17.8
Thus, the two numbers are 17.8 and 32.2 respectively.
Solution 6
Let the two numbers be x and y.
Then,
x + y = 8 …..(i)
x2 - y2 = 32 …..(ii)
⟹ (x - y)(x + y) = 32
⟹ x - y = 4 ….. (iii)
Adding (i) and (iii), we get
2x = 12 ⟹ x = 6
From (i), y = 8 - x = 8 - 6 = 2
Therefore, the numbers are 6 and 2.
Solution 7
Two numbers are x and y respectively such that x > y.
Then,
x - y = 4 ….(i)
⇒ x = 4 + y
And,
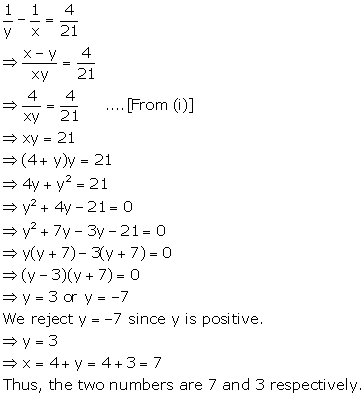
Solution 8
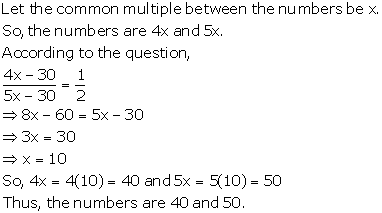
Solution 9
Let the numerator and denominator a fraction be x and y respectively .
According to the question,
![]()
3x - 2y = -8...(1)
And,
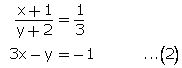
Now subtracting,
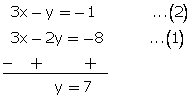
From (1) ,
3x - 2 (7) = -8
3x = -8 + 14
x = 2
Required fraction = ![]()
Solution 10
Let the numerator and denominator of a fraction be x and y respectively .Then the fraction will be ![]()
According to the question,
x + y = 7...(1)
5y - 4x = 8...(2)
Multiplying equation no. (1) by 4 and add with (2),
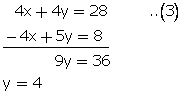
From (1)
x + 4 = 7
x = 3
Required fraction = ![]()
Solution 11

Solution 12

Solution 13
Let the digit at unit’s place be x and the digit at ten’s place y.
Required no. = 10y + x
If the digit’s are reversed,
Reversed no. = 10y + x
According to the question,
x + y = 5...(1)
and,
(10y + x) - (10x + y) = 27
![]()
Now adding the two equation,
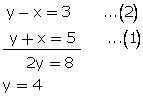
From (1)
x + 4 = 5
x = 1
Require no is
10 (4) + 1 = 41
Solution 14
Let the digit at unit’s place be x and the digit at ten’s place be y.
Required no. = 10y + x
If the digit’s are reversed
Reversed no. = 10x + y
According to the question,
x + y = 7...(1)
and,
10x + y - 2 = 2(10y + x).
8x - 19y = 2...(2)
Multiplying equation no. (1) by 19.
![]()
Now adding equation(2) and (3)
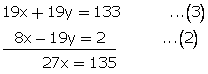
x = 5
From (1)
5 +y = 7
y = 2
Required number is
10(2) + 5
= 25.
Solution 15
Let the digit at unit’s place be x and the digit at ten’s place be y.
Required no. = 10y + x
According to the question
y = 3x ![]() 3x - y = 0...(1)
3x - y = 0...(1)
and,10y + x + x = 32
10y + 2x = 32...(2)
Multiplying equation no. (1) by 10
![]()
Now adding (3)and(2)
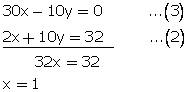
From (1),we get
y = 3(1) = 3
Required no is
10(3) + 1 = 31
Solution 16
Let the digit a unit’s place be x and the digit at ten’s place be y.
Required no. = 10y + x.
According to the question,
y - 2x = 2
-2x + y = 2...(1)
and,
(10x + y) -3 (y + x) = 5
7x - 2y = 5...(2)
Multiplying equation no. (1) by 2.
![]()
Now adding (2)and(3)
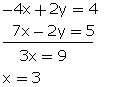
From (1) ,we get
-2(3) + y = 2
![]() y = 8
y = 8
Required number is
10(8) + 3 = 83.
Solution 17
Let present age of A = x years
And present age of B = y years
According to the question,
Five years ago,
x - 5 = 4(y - 5)
x - 4y = -15...(1)
Five years later,
x + 5 = 2(y + 5)
![]()
Now subtracting (1)from(2)
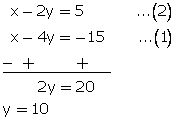
From (1)
x - 4 (10) = -15
x = 25
Present ages of A and B are 25 years and 10 years respectively.
Solution 18
Let A’s presentage be x years
and B’s present age be y years
According to the question
x = y + 20
x - y = 20...(1)
Five years ago,
x - 5 = 3(y - 5)
![]()
Subtracting (1)from(2),
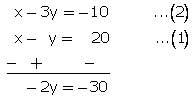
y = 15
From (1)
x = 15 + 20
x = 35
Thus, present ages of A and B are 35 years and 15 years.
Solution 19
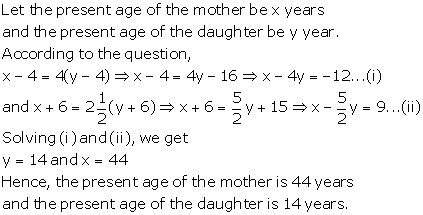
Solution 20
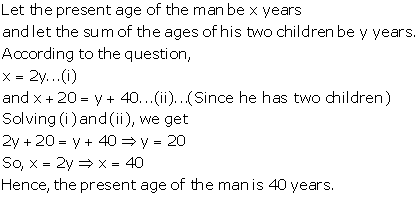
Solution 21
Let A’s annual in come = Rs.x
and B’s annual income = Rs. y
According to the question,
![]()
4x - 3y = 0...(1)
and,![]()
7x - 5y = 10000...(2)
Multiplying equation no. (1) by 7 and (2) by 4.and subtracting (4) from (3)
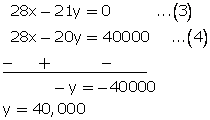
From (1)
4x - 3 (40000) = 0
x = 30000
Thus, A’s income in Rs. 30,000 and B’s income is Rs. 40,000.
Solution 22
Let the no. of pass candidates be x
and the no. of fail candidates be y.
According to the question,
![]()
x - 4y = 0...(1)
and![]()
x - 5y = -30...(2)
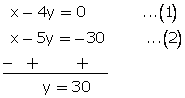
From (1)
- 4(30) = 0
x = 120
Total students appeared = x + y
= 120 + 30
= 150
Solution 23
Let the numberof pencils with A = x
and the number of pencils with B = y.
If A gives 10 pencils to B,
y + 10 = 2(x - 10)
2x - y = 30...(1)
If B gives to pencils to A
y - 10 = x + 10
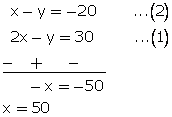
From (1)
2(50) - y = 30
y = 70
Thus, A has 50 pencils and B has 70 pencils.
Solution 24
Let the number of adults = x
and the number of children = y
According to the question,
x + y = 1250...(1)
and 75x + 25y = 61250
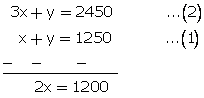
x = 6000
From (1)
600 + y = 1250
y = 650
Thus, number of adults = 600
and the number of children = 650.
Solution 25
Let Rohit has Rs. x
and Ajay has Rs. y
When Ajay gives Rs. 100 to Rohit
x + 100 = 2(y - 100)
x - 2y = -300...(1)
When Rohit gives Rs. 10 to Ajay
6(x-10) = y + 10
6x - y = 70...(2)
Multiplying equation no. (2) By 2.
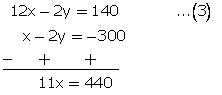
x = 40
From (1)
40 - 2y = -300
![]() -2y = -340
-2y = -340
![]() y = 170
y = 170
Thus, Rohit has Rs. 40
and Ajay has Rs. 170
Solution 26

Solution 27
Let the digit at ten’s place be x
And the digit at unit’s place be y
Required number = 10x + y
When the digits are interchanged,
Reversed number = 10y + x
According to the question,
7(10x + y) = 4(10y + x)
66x = 33y
2x - y = 0...(1)
Also,
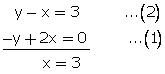
From (1) 2(3) - y = 0
y = 6
Thus, Required number = 10(3) + 6 = 36
Solution 28
Let, the fare of ticket for station A be Rs. x
and the fare of ticket for station B be Rs. y
According, to the question
2x + 3y = 77....(1)
and3x+5y = 124...(2)
Multiplying equation no. (1) by 3 and (2) by 2.
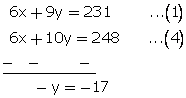
y = 17
From (1) 2x + 3 (17) = 77
2x = 77 - 51
2x = 26
x = 13
Thus, fare for station A = Rs. 13
and, fare for station B = Rs. 17.
Solution 29
_files/20140922192829_image002.gif)
Solution 30
Let the quantity of 90% acid solution be x litres and
The quantity of 97% acid solution be y litres
According to the question,
x + y = 21...(1)
and 90% of x + 97% of y = 95% of 21
90x + 97y = 1995...(2)
Multiplying equation no. (1) by90, we get,
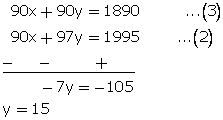
From (1)x + 15 = 21
x = 6
Hence, 90% acid solution is 6 litres and 97% acid solution is 15 litres.
Solution 31
_files/20140922201657_image002.gif)
Simultaneous (Linear) Equations (Including Problems) Exercise Test Yourself
Solution 1
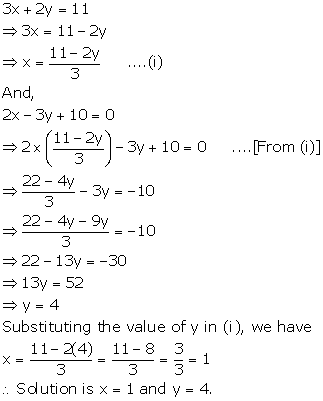
Solution 2
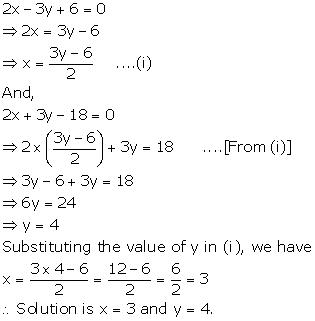
Solution 3
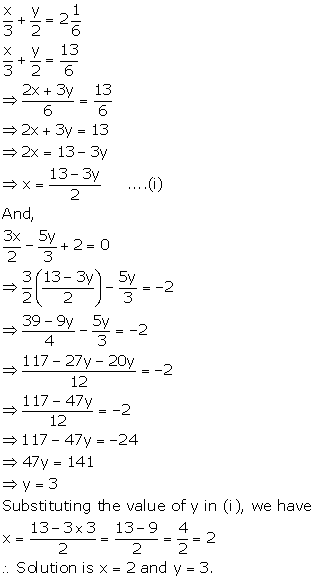
Solution 4
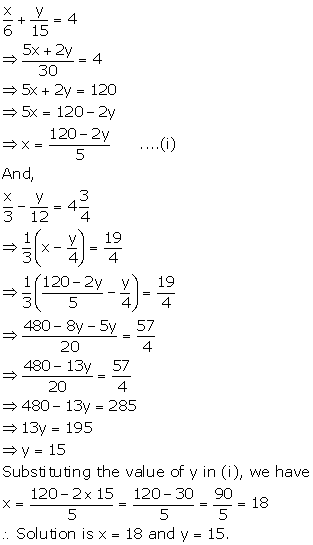
Solution 5
_files/20140922185444_image018.gif)
Solution 6
_files/20140922185444_image020.gif)
Solution 7
_files/20140922185444_image022.gif)
Solution 8
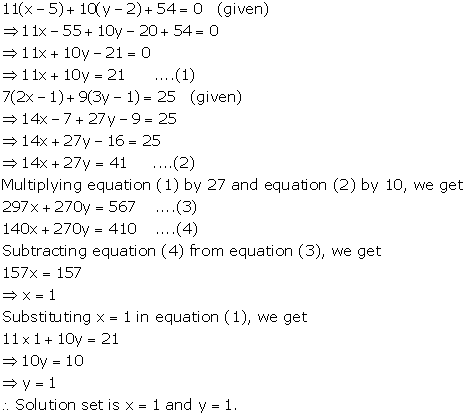
Solution 9
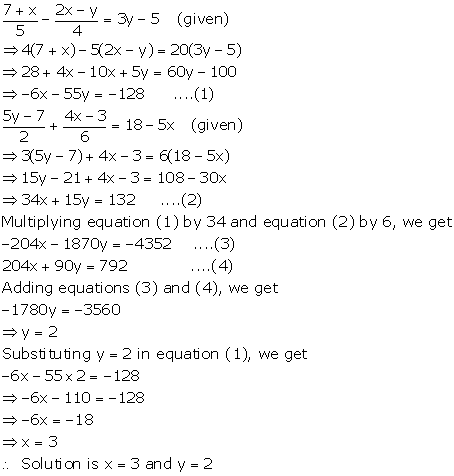
Solution 10
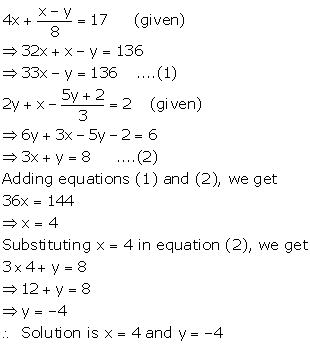
Solution 11
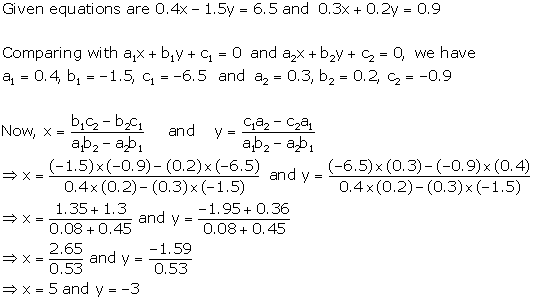
Solution 12
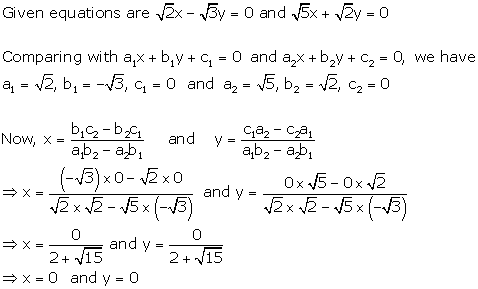
Solution 13
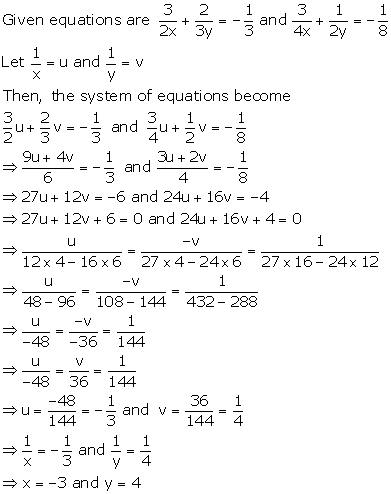
Solution 14
_files/20140922201657_image016.gif)
Solution 15

Solution 16
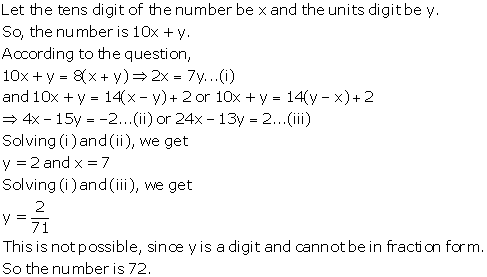
Solution 17
Let the cost price of article A = Rs. x
and the cost price of articles B = Rs. y
According to the question,
(x + 5% of x) +(y + 7% of y) = 1167
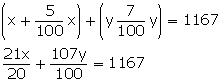
105x + 107y = 1167...(1)
and ![]()
107x + 105y = 116500...(2)
Adding(1) and (2)
212x + 212y = 233200
x + y = 1100...(3)
subtracting (2)from (1)
-2x + 2y = 200
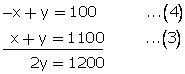
y = 600
from (3)
x +600 = 1100
x = 500
Thus, cost price of article A is Rs. 500.
and that of article B is Rs. 600.
Solution 18
Let Pooja’s 1 day work = ![]()
and Ritu’s 1 day work = ![]()
According the question,
![]()
and,![]()
![]()
Using the value of y from (2) in (1)
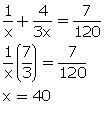
From (2) ![]()
y = 30
Pooja will complete the work in 40 days and Ritu will complete the work in 30 days.
Solution 19
Weight of Mr. Ahuja = x kg
and weight of Mrs. Ahuja = y kg.
After the dieting,
x - 5 = y
x - y = 5...(1)
and, ![]()
7x - 8y = -32...(2)
Multiplying equation no. (1) by 7, we get
![]()
Now subtracting (2) from (3)
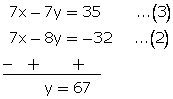
From (1)
x - 67 = 5![]() x = 72
x = 72
Thus, weight of Mr. Ahuja = 72 kg.
and that of Mr. Anuja = 67 kg.
Solution 20
_files/20140922201657_image018.gif)
Solution 21
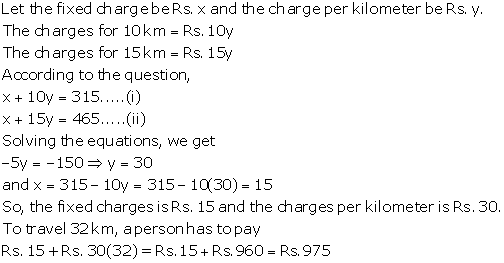
Solution 22
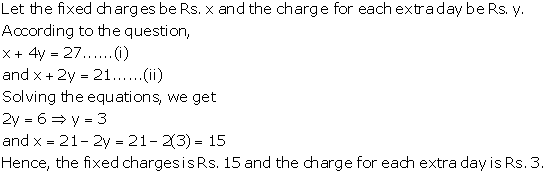
Solution 23

Solution 24


