Class 9 SELINA Solutions Chemistry Chapter 7: Study of Gas Laws
Study of Gas Laws Exercise Ex. 7
Solution A. 1
(iii) Straight line parallel to the X-axis.
Solution A. 2
(ii) 27°C = 27 + 273 = 300 K
Solution A. 3
(iv) Charles
Solution A. 4
(ii) 1/2 times
Solution A. 5
Correct option: (iii) - Kelvin
Solution A. 6
Correct option: (ii) - 373 K
Solution A. 7
Correct option: (iii) - Boyle's law
Solution A. 8
Correct option: (iii) - Charles' law
Solution A. 9
Correct option: (iv) - 20 litres
Solution A. 10
Correct option: (i) - 273 K and 760 mm
Solution B. 1
|
Column A |
Column B |
|
(a) cm3 |
Volume |
|
(b) Kelvin |
Temperature |
|
(c) Torr |
Pressure |
|
(d) Boyle's law |
PV = P1 V1
|
|
(e) Charles's law |
|
Solution B. 2
- Absolute temperature
- Absolute zero
- Volume
- 273
Solution B. 3
- Volume of a gas is directly proportional to the pressure at constant temperature.
- Volume of a fixed mass of a gas is inversely proportional to the temperature, the pressure remaining constant.
- -273°C is equal to zero Kelvin.
- Standard temperature is 0°C.
- The boiling point of water is -373 K.
Solution B. 4
- Three variables for gas laws: Volume (V), Pressure (P), Temperature (T)
- SI units of these variables:
For volume: Cubic metre (m3)
For pressure: Pascal (Pa)
For temperature: Kelvin (K)
Solution B. 5
- °C = O°C
- K = 273 K
- 1 atm
- 760 mmHg
- 76 cmHg
- 1 torr = 133.32 Pascal
Solution B. 6
- Volume of gas is zero.
- Absolute temperature is 7 + 273 = 280 K.
- The gas equation is
![]()
- Ice point = 0 + 273 = 273 K
- Standard temperature is taken as 273 K or O°C.
Standard pressure is taken as 1 atmosphere (atm) or 760 mmHg.
Solution C. 1
Gas is a state of matter in which interparticle attraction is weak and interparticle space is so large that the particles become completely free to move randomly in the entire available space.
Solution C. 2
Diffusion is the process of gradual mixing of two substances, kept in contact, by molecular motion.
Example:
If a jar of chlorine is opened in a large room, the odorous gas mixes with air and spreads to every part of the room. Although chlorine is heavier than air, it does not remain at the floor level but spreads throughout the room.
Solution C. 3
Temperature affects the kinetic energy of molecules. So, molecular motion is directly proportional to temperature.
Solution C. 4
Absolute zero
The temperature -273°C is called absolute zero.
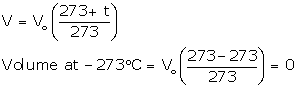
Absolute or Kelvin scale of temperature
The temperature scale with its zero at -273°C and each degree equal to one degree on the Celsius scale is called Kelvin or the absolute scale of temperature.
Conversion of temperature from Celsius scale to Kelvin scale and vice versa
The value on the Celsius scale can be converted to the Kelvin scale by adding 273 to it.
Example:
20°C = 20 + 273 = 293 K
Solution C. 5
- Standard or Normal Temperature and Pressure (STP or NTP)
The pressure of the atmosphere which is equal to 76 cm or 760 mm of mercury and the temperature is 0°C or 273 K is called STP or NTP. The full form of STP is Standard Tempe rature and Pressure, while that of NTP is Normal Temperature and Pressure.
Value: The standard values chosen are 0°C or 273 K for temperature and 1 atmospheric unit (atm) or 760 mm of mercury for pressure.
The standard values chosen are 0°C or 273 K for temperature and 1 atmospheric unit (atm) or 760 mm of mercury for pressure.
|
Standard temperature = 0°C = 273 K Standard pressure = 760 mmHg = 76 cm of Hg = 1 atmospheric pressure (atm) |
- The volume of a given mass of dry enclosed gas depends on the pressure of the gas and the temperature of the gas in Kelvin, so to express the volume of the gases, we compare these to STP.
Solution C. 6
- Charles's law
- Boyle's law
Solution C. 7
Temperature on the Kelvin scale (K)
= 273 + temperature on the Celsius scale
Or K = 273 + °C
273°C in Kelvin
t°C = t K - 273
273°C = t K - 273
t K = 273 + 273 = 546 K
∴ 273°C = 546 K
Solution C. 8
- Pressure will double.
- Pressure remains the same.
Solution C. 9
- The behaviour of gases shows that it is not possible to have temperature below 273.15°C. This act has led to the formulation of another scale known as the Kelvin scale. The real advantage of the Kelvin scale is that it makes the application and the use of gas laws simple. Even more significantly, all values on the Kelvin scale are positive.
- The boiling point of water on the Kelvin scale is 373 K. Now, K = °C + 273 and °C = K - 273.
The Kelvin scale can be converted to the degree Celsius scale by subtracting 273 So, the boiling point of water on the centigrade scale is 373 K - 273 = 100°C.
Solution C. 10
- The advantage of the Kelvin scale is that it makes the application and use of gas laws simple. Of more significance is that all values on the scale are positive, removing the problem of negative (-) values on the Celsius scale.
- The mass of a gas per unit volume is small because of the large intermolecular spaces between the molecules. Therefore, gases have low density. In solids and liquids, the mass is higher and intermolecular spaces are negligible.
- At a given temperature, the number of molecules of a gas striking against the walls of the container per unit time per unit area is the same. Thus, gases exert the same pressure in all directions.
- Because the volume of a gas changes remarkably with a change in temperature and pressure, it becomes necessary to choose a standard value of temperature pressure.
- According to Boyle's law, the volume of a given mass of a dry gas is inversely proportional to its pressure at constant temperature.

When a balloon is inflated, the pressure inside the balloon decreases, and according to Boyle's law, the volume of the gas should increase. But this does not happen. On inflation of a balloon along with reduction of pressure of air inside the balloon, the volume of air also decreases, violating Boyle's law.
- Atmospheric pressure is low at high altitudes. The volume of air increases and air becomes less dense because volume is inversely proportional to density. Hence, lesser volume of oxygen is available for breathing. Thus, mountaineers have to carry oxygen cylinders with them.
- Interparticle attraction is weak and interparticle space is large in gases because the particles are completely free to move randomly in the entire available space and takes the shape of the vessel in which the gas is kept.
Solution D. 1
- Gases are made of tiny particles which move in all possible directions at all possible speeds. The size of molecules is small as compared to the volume of the occupied gas.
- There is no force of attraction between gas particles or between the particles and the walls of the container. So, the particles are free to move in the entire space available to them.
- The moving particles of gas collide with each other and with the walls of the container. Because of these collisions, gas molecules exert pressure. Gases exert the same pressure in all directions.
- There is large interparticle space between gas molecules, and this accounts for high compressibility of gases.
- Volume of a gas increases with a decrease in pressure and increase in temperature.
- Gases have low density as they have large intermolecular spaces between their molecules.
- Gases have a natural tendency to mix with one and other because of large intermolecular spaces. So, two gases when mixed form a homogeneous gaseous mixture.
- The intermolecular space of a gas is reduced because of cooling. Molecules come closer resulting in liquefaction of the gas.
Solution D. 2
Boyle's law on the basis of the kinetic theory of matter:
- According to the kinetic theory of matter, the number of particles present in a given mass and the average kinetic energy is constant.
- If the volume of the given mass of a gas is reduced to half of its original volume, then the same number of particles will have half the space to move.
- As a result, the number of molecules striking the unit area of the walls of the container at a given time will double and the pressure will also double.
- Alternatively, if the volume of a given mass of a gas is doubled at constant temperature, the same number of molecules will have double the space to move.
- Thus, the number of molecules striking the unit area of the walls of a container at a given time will become one-half of the original value.
- Thus, pressure will also get reduced to half of the original pressure. Hence, it is seen that if the pressure increases, the volume of a gas decreases at constant temperature, which is Boyle's law.
Solution D. 3
Charles's law on the basis of the kinetic theory of matter:
According to the kinetic theory of matter, the average kinetic energy of gas molecules is directly proportional to the absolute temperature. Thus, when the temperature of a gas is increased, the molecules would move faster and the molecules will strike the unit area of the walls of the container more frequently and vigorously. If the pressure is kept constant, the volume increases proportionately. Hence, at constant pressure, the volume of a given mass of a gas is directly proportional to the temperature (Charles's law).
Solution D. 4
- The temperature scale with its zero at -273°C and where each degree is equal to the degree on the Celsius scale is called the absolute scale of temperature.
- The temperature -273°C is called absolute zero. Theoretically, this is the lowest temperature which can never be reached. All molecular motion ceases at this temperature.
- The temperature -273°C is called absolute zero.
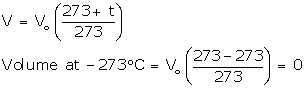
Solution D. 5
- Boyle's law: At constant temperature, the volume of a definite mass of any gas is inversely proportional to the pressure of the gas.
Or
Temperature remaining constant, the product of the volume and pressure of the given mass of a dry gas is constant
i. Mathematical representation:
According to Boyle's Law,
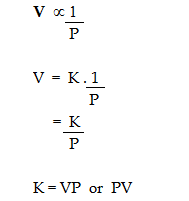
where K is the constant of proportionality.
If V' and P' are some other volume and pressure of the gas at the same temperature, then
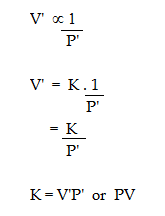
ii. Graphical representation of Boyle's Law:
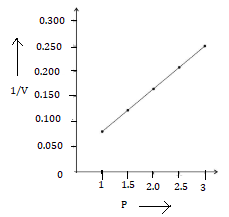
1. ![]() : Variation in volume (V) plotted against (1/P) at a constant temperature: A straight line passing through the origin is obtained.
: Variation in volume (V) plotted against (1/P) at a constant temperature: A straight line passing through the origin is obtained.
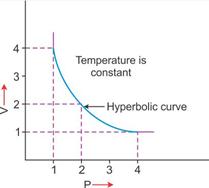
|
|
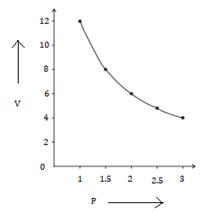
2. V vs P: Variation in volume (V) plotted against pressure (P) at a constant temperature: A hyperbolic curve in the first quadrant is obtained.
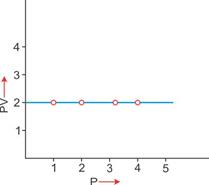
|
|
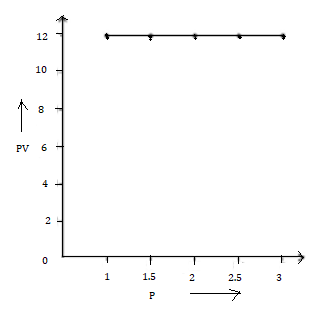
3. PV vs P: Variation in PV plotted against pressure (P) at a constant temperature: A straight line parallel to the X-axis is obtained.
|
|
iii. Significance of Boyle's law:
According to Boyle's law, on increasing pressure, volume decreases. The gas becomes denser. Thus, at constant temperature, the density of a gas is directly proportional to the pressure.
At higher altitude, atmospheric pressure is low so air is less dense. As a result, lesser oxygen is available for breathing. This is the reason mountaineers carry oxygen cylinders.
Solution D. 6
Charles's Law
At constant pressure, the volume of a given mass of a dry gas increases or decreases by 1/273rd of its original volume at 0°C for each degree centigrade rise or fall in temperature.
|
V ∝ T (at constant pressure) |
At temperature T1 (K) and volume V1 (cm3):
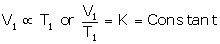 ...(i)
...(i)
At temperature T2 (K) and volume V2 (cm3):
![]() ….(ii)
….(ii)
From (i) and (ii),
![]()
For Temperature = Conversion from Celsius to Kelvin
1 K = °C + 273
Example:
20°C = 20 + 273 = 293 K
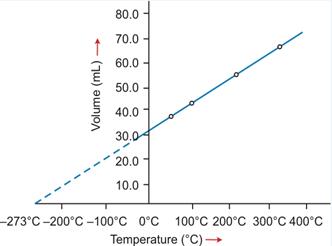
Graphical representation of Charles's law
T vs V: The relationship between the volume and the temperature of a gas can be plotted on a graph. A straight line is obtained.
|
Graphical representation of Charles's law |
Significance of Charles's Law: The volume of a given mass of a gas is directly proportional to its temperature; hence, the density decreases with temperature. This is the reason that
(a) Hot air is filled in balloons used for meteorological purposes. (b) Cable wires contract in winters and expand in summers.
Solution D. 7
Gases such as nitrogen and hydrogen are collected over water as shown in the diagram. When the gas is collected over water, the gas is moist and contains water vapour. The total pressure exerted by this moist gas is equal to the sum of the partial pressures of the dry gas and the pressure exerted by water vapour. The partial pressure of water vapour is also known as aqueous tension.
|
Collection of gas over water |
Ptotal = Pgas + Pwater vapour
Pgas = Ptotal- Pwater vapour
Actual pressure of gas = Total pressure - Aqueous tension
Solution D. 8
The phenomenon is diffusion. In air, gas molecules diffuse to mix thoroughly. Hence, we can smell hydrogen sulphide gas from a distance in the laboratory.
Solution E. 1
(a) Boyle's law: Volume of a given mass of a dry gas is inversely proportional to its pressure at constant temperature.
(b) PV isotherm for Boyle's law:

Solution E. 2
(a) Charles' law
(b) Mathematical expression of Charles' law:
Let V0 be the volume of a fixed mass of a gas at 0° C, and let V be its volume at temperature t° C at constant pressure. Then, according to Charles' law,
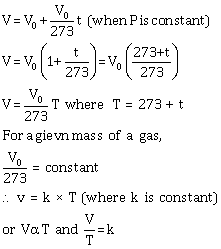
![]()
(c) Application / use where Charles' law is employed:
Volume of a given mass of a gas is directly proportional to its temperature, hence density decreases with an increase in temperature. This is the reason why hot air is filled into balloons used for meteorological purposes.
Solution E. 3
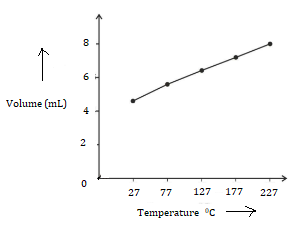
(a) The graph between V and T is a straight line.
(b) No. The line does not pass through the origin.
(c) Charles' law is obeyed as V α T.
Solution Num 1
293 K in °C
t°C = 293 - 273
t°C = 20°C
∴ 293 K = 20°C
Solution Num 2
V1 = 500 dm3
P1 = 1 bar
T1 = 273 K
V2 = 500 dm3
T2 = 273 K
P2= ?
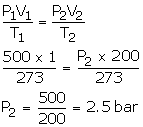
Solution Num 3
V = 2 litres
P = 760 mm
V1 = 4000 m3 [1 dm3 = 4 litres]
P1= ?
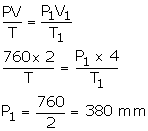
Solution Num 4
According to Boyle's law:
V1 = 800 cm3
P1 = 654 mm
P2= ?
V2 = reduced volume = 40% of 800 cm3
Remaining volume is 60% of its original volume.
= 800 × 60 / 100 = 480 cm3
⇒ P2 = 654 × 800 / 480 = 1090 mm
Solution Num 5
(a)
|
Pressure in atmosphere |
Volume in litres |
1/V |
PV |
|
1.0 |
12 |
0.08 |
12 |
|
1.5 |
8.0 |
0.125 |
12 |
|
2.0 |
6.0 |
0.17 |
12 |
|
2.5 |
4.8 |
0.21 |
12 |
|
3.0 |
4.0 |
0.25 |
12 |
1. P vs V
2. P vs 1/V
3. PV vs P
(b) Applying Boyle's law,
P1V1 = P2V2
From the given information let us take P1 = 3 atm and V1 = 4 L
P2 = 2.3, let us consider V2= ?
P1V1 = P2V2
3×4 = 2.3 × V2
V2 = 3×4 / 2.3 = 5.2 L
Thus, at 2.3 atmospheric pressure, the volume will be 5.2 Litres,
|
Pressure in atmospheres |
Volume in litres |
|
1.0 |
12 |
|
1.5 |
8.0 |
|
2.0 |
6.0 |
|
2.3 |
5.2 |
|
2.5 |
4.8 |
|
3.0 |
4 |
Solution Num 6

Solution Num 7
V = 20 litre
P = 29 atm
P1 = 1.25 atm
V1 =?
T = T1
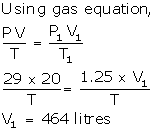
Solution Num 8
Initial volume = V1 = 561 dm3
Final volume = V2 = 748 dm3
Difference in volume = 748 - 561 = 187 dm3
As the temperature is constant,
Decrease in pressure percentage =
![]()
Solution Num 9
V = 88 cm3
P = 770 mm
P1 = 880 mm
V1= ?
T = T1

Volume diminishes = 88 - 77 = 11 cm3
Solution Num 10
Let volume = 100 ml
T = 240 K
Volume increased = x ml
New volume = 100 + x ml
T1 = 400 K
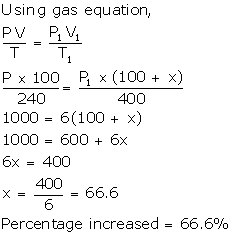
Solution Num 11
(a) V1 = 0.4 L
V2 = 0.4 × 2L
T1 = 17°C (17 + 273) = 290 K
T2= ?
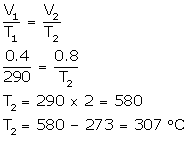
(b) V1 = 0.4 L
V2 = 0.2 L
T1 = 17°C (17 + 273) = 290 K
T2= ?
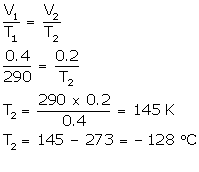
Solution Num 12
V1 = 143 cm3
T1 = 27oC = 27+273 = 300K
P1 = 700 mm Hg
T2 = 300K
P2= 280 mm Hg
V2= ?
![]()
![]()
![]() 2 = 357.5 cm3
2 = 357.5 cm3
Solution Num 13
V = 500 cm3
Normal temperature, t = 0°C = 0 + 273 K
V1 = Reduced volume + 20% of 500 cm3
![]()
Net, V1 = 500 - 100 = 400 cm3
T1= ?
P = P1
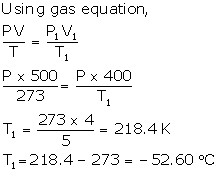
Solution Num 14
V1 = X
P1 = 1 atm
V2= ?
T2 = 3 T1
P2 = 2 atm
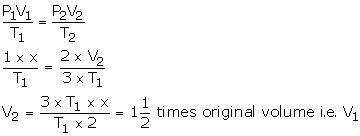
Solution Num 15
V = 30 cm3
P = 740 mm
T = 288 K
P1 = 760 mm
V1= ?
T1 = 273 K
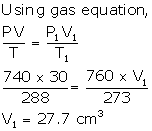
Solution Num 16
V1 = V1
P1 = 760 atm
T1 = 273 K
V2 = 2V1
T2 =?
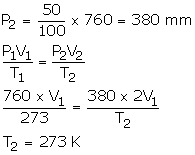
Solution Num 17
V = 100 cm3
P = 760 mm
T = 273 K
V1= ?

Solution Num 18
Let the original volume (V) = 1 and
the original pressure (P) = 1 and
the temperature given (T) = -15°C = -15 + 273 = 258 K
V1 or new volume after heating = original volume + 50% of original volume
![]()
P1 or decreased pressure = 60%
![]()
T1 = to be calculated
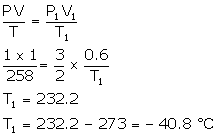
Solution Num 19
V = 2 litres
P = 100 Pa
T = 300 K

T1 = 75 - 273 = -198°C
Solution Num 20
V1 = 2500 cm3
P1 = 1 atm = 760 mm
T1 = 273 K
V2= ?
T2 = 273 K

Solution Num 21
V1 = 714.29 cm3
P1 = P2 = P
T1 = 273 K
V2 = 2500 cm3
T2= ?

Solution Num 22
- V1 = V2 = V
P1 = 100 cmHg
T1 = 273 K
P2 = 10 cmHg
T2= ?
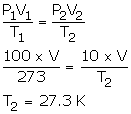
- V1 = V2 = V
P1 = 100 cmHg
P2= ?
T1 = 273 K
T2 = 373 K

Solution Num 23
Capacity of the cylinder V = 10000 litres
P = 800 mm
T = -3 °C = -3 + 273 = 270 K
P1 = 400 mm Hg
T1 = 0 °C = 0 + 273 = 273 K
V1 = ?
PV / T = P1V1 / T1
![]()
![]()
Solution Num 24
![]()
P1 = 1 atm = 760 mm Hg
T1 = 27 C = 273 + 27 = 300 K
P2 = 3 atm = 2280 mm Hg
T2= ?
P1/T1 = P2/T2
760 / 300 = 2280 / T2
T2 = 2280 × 300 / 760 = 900 K
Solution Num 26
V1 = 22.4 litres
P1 = 1 atm
T1 = 273 K
V2 =?
T2 = 300 K
P2 = 4 atm
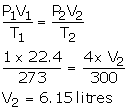
Solution Num 27
- V = 1.2 litres
P = 748 mmHg
T = 298 K
P1 = 760 mmHg
T1 = 273 K
V1= ?
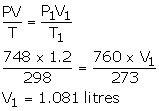
- V = 1.25 litres
P = 760 mmHg
T = 273 K
P1 = 760 mmHg
T1 = 273 K
V1= ?
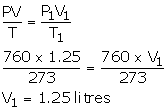
1.25 litres O2 will have greater volume than 1.2 litres N2.
Solution Num 28
V = 50 cm3
P = 750 - 14 = 736 mm
T = 290 K
P1 = 760 mm
V1= ?
T1 = 273 K
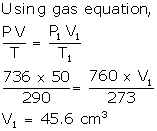
Solution Num 29
Pressure due to dry air,
P = 750 - 12 = 738 mm
V = 28 cm3
T = 14°C = 14 + 273 = 287 K
P1 = 760 mmHg
V1= ?
T1 = 0°C = 273 K
Using gas equation,
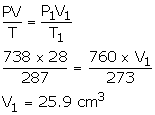
Solution Num 30
P = 14.9 atm
V = 28 cm3
T = ?
P1 = 12 atm
V = V1
T1 = 300 K
Using gas equation,
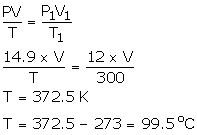
Solution Num 31
Step 1:
V1 = 20 litres
P1 = 700 mm
T1 = 300 K
V2= ?
T2 = 273 K
P2 = 760 mm
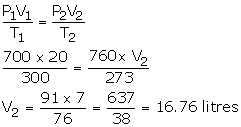
Step 2:
22.4 litres of the gas at STP weighs = 70 g
16.76 litres of the gas has weight at STP =
![]()