Class 10 SELINA Solutions Physics Chapter 5 - Refraction Through A Lens
Refraction Through A Lens Exercise Ex. 5A
Solution A.1
(d) concavo-convex

The given figure represents concavo – convex lens.
Solution A.2
(c) one surface plane and the other surface concave
A plano-concave lens has one surface plane and the other surface concave.
Solution A.3
(b) a convexo-concave lens is thicker in the middle and has a converging action.
A convexo-concave lens is thinner in the middle and has a diverging action like a concave lens.
Solution A.4
(a) downward, upward
A convex lens in its upper part has a prism with its base downward and a concave lens in its upper part has a prism with its base upward.
Solution A.5
(d) (2)
Convex lens converges the incident rays towards the principal axis whereas concave lens diverges is the correct statement.
Solution A.6
(b) its first focus
If a ray passes through the first focus of a convex lens, it emerges parallel to the principal axis after refraction.
Solution A.7
(c) Its second focus
After refraction by a convex lens, parallel rays of light either meet at a point on the principal axis or appear to come from a point on the principal axis. This is referred to as the lens's second focus.
Solution A.8
(c) the radius of curvature of the two surfaces
A lens is called equi-convex or equi-concave when the radius of curvature of the two surfaces of the lens are equal.
Solution A.9
(d) both (a) and (c)
The focal length of a lens depends upon the refractive index of the material of lens relative to its surrounding medium and the radius of curvature of the two surfaces of lens.
Solution A.10
(a) increases
The focal length increases if a lens is placed in water instead of air.
Solution A.11
(d) does not change, decreases
The focal length of a convex lens depends on its curvature, and it does not change by covering half. However, the intensity of the image will decrease because fewer light rays pass through.
Solution A.12
(b) more
A thin convex lens has a smaller curvature on its surfaces compared to a thick convex lens. The focal length of a convex lens is inversely proportional to its curvature. This means a lens with a higher curvature will have a shorter focal length. Therefore, a thin convex lens with a smaller curvature will have a greater focal length compared to a thick convex lens which will have higher curvature.
Solution A.13
(d) radius of curvature
The radius of the sphere, which is part of the lens's surface, is called the radius of curvature of that surface.
Solution A.14
(b) when we say focal length of a lens, we mean the first focal length of the lens.
A lens actually has two focal points, one on each side. These are called the first focal point (F1) and the second focal point (F2). The focal length refers to the distance between either the first focal point (F1) or the second focal point (F2) and the center of the lens, and they typically have the same value (numerically) for a thin lens in air.
Thus, when we say focal length of a lens, it can refer to the distance from either F1 or F2 to the center, not necessarily just the first focal length.
Solution B.1
A lens is a transparent refracting medium bounded by two curved surfaces which are generally spherical.
Solution B.2(i)
Equiconvex lens is converging.
Solution B.2(ii)
The concavo-convex lens is a converging lens. This is because it is thicker at the middle and thinner at edges allowing it to converge all the light that is incident on it.
Solution B.3
A lens is called an equiconvex or equiconcave when radii of curvature of the two surfaces of lens are equal.
Solution B.4
The distance from the optical centre O of the lens to its second focal point is called the focal length of the lens.
Solution B.5
A plane passing through the focal point and normal to the principal axis of the lens is called the first focal plane.
Solution B.6
(i) If a lens has both its focal length equal medium is same on either side of lens.
(ii)If a ray passes undeviated through the lens it is incident at the optical centre of the lens.
Solution B.7
(a) If half part of a convex lens is covered, the focal length does not change, but the intensity of image decreases.
(b) A convex lens is placed in water. Its focal length will increase.
(c) The focal length of a thin convex lens is more than that of a thick convex lens.
Solution C.1
Lenses are of two types :
(i)Convex or converging lens, and
(ii)Concave or diverging lens.
![]() convex lens
convex lens![]() concave lens
concave lens
Solution C.2
Convex lens:
(a) Thick in the middle thinner at the edges.
(b)
(i)It converge the incident rays towards the principal axis.
(ii)It has a real focus.
Concave lens:
(a) Thin in the middle thicker at the edges.
(i)It diverges the incident rays away from the principal axis.
(ii)It has a virtual focus.
Solution C.3
It is the line joining the centers of curvature of the two surfaces of the lens.
Solution C.4
It is point on the principal axis of the lens such that a ray of light passing through this point emerges parallel to its direction of incidence.
It is marked by letter O in the figure. The optical centre is thus the centre of the lens.
Solution C.5
(a) This point is known as Optical centre.
(b)
Solution C.6
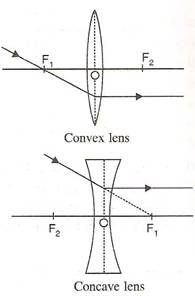
A light ray can pass through a lens from either direction. Therefore, a lens has two principal foci.
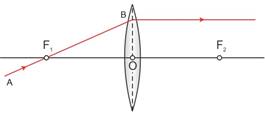
For a convex lens, the first focal point is a point F1 on the principal axis of the lens such that the rays of light starting from it or passing through it, after refraction through lens, become parallel to the principal axis of the lens.
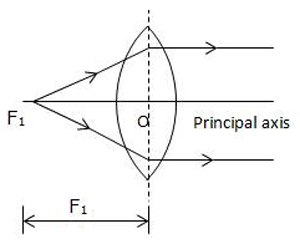
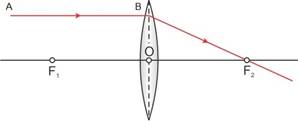
The second focal point for a convex lens is a point F2 on the principal axis such that the rays of light incident parallel to the principal axis, after refraction from the lens, pass through it.
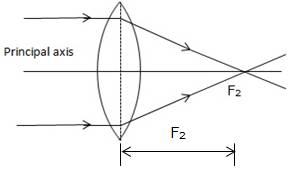
Solution C.7
A light ray can pass through a lens from either direction. Therefore, a lens has two principal foci.
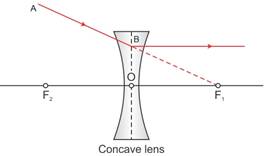
For a concave lens, the first focal point is a point F1 on the principal axis of the lens such that the incident rays of light appearing to meet at it, after refraction from the lens become parallel to the principal axis of the lens.

The second focal point for a concave lens is a point F2 on the principal axis of the lens such that the rays of light incident parallel to the principal axis, after refraction from the lens, appear to be diverging from this point.
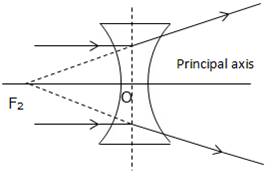
Solution C.8
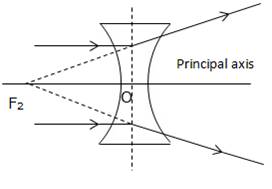
Concave lens representing second focus
Solution C.9
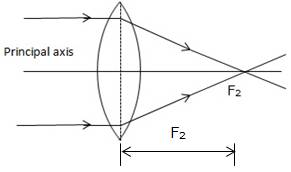
Convex lens representing second focus
Solution D.1
Concave lens will show the divergent action on a light beam.
Solution D.2

As shown in the figure the convex lens has two glass prisms and one glass slab. One of the glass prisms is situated above the glass slab and one below the slab.
Solution D.3
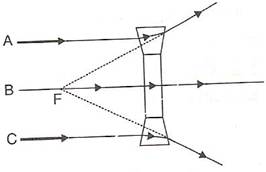
As shown in the figure the concave lens has two glass prisms and one glass slab. One of the glass prisms is situated above the glass slab and one below the slab.
Solution D.4
If a parallel beam of light is incident on a convex lens then the upper part of the lens bends the incident ray downwards. The lower part bens the ray upwards while the central part passes the ray undeviated.
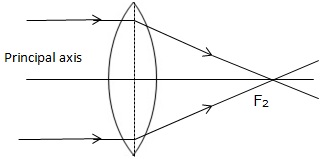
Convex lens
But in case of a concave lens the upper part of the lens bends the incident ray upwards and lower part bends the ray downwards while the central part passes the ray undeviated.
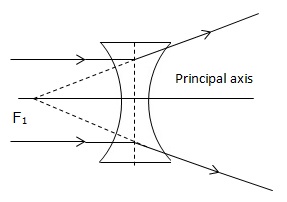
Concave lens
Solution D.5
(a)
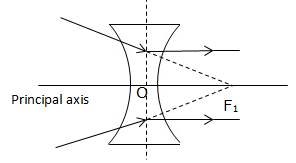
(b) The point where incident ray when produced meets the principal axis is called first focus.
Solution D.6
(a)

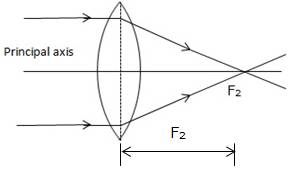
(b) The point where incident ray passes through a point on the principal axis is called first focus.
Solution D.7
Such a point will be second focus.
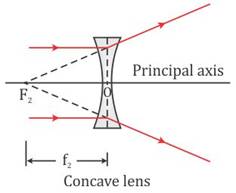
Solution D.8
It appears to come from 'Second Focus'.
Solution D.9
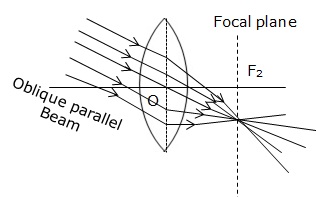
Refraction of an oblique parallel beam by a convex lens.
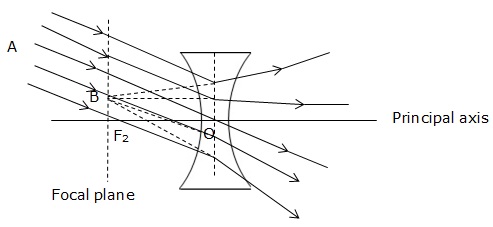
Refraction of an oblique parallel beam by a concave lens
Solution D.10
(i)The combination forms convex lens.
(ii)XX' is known as principal axis.
(iii)The complete diagram is
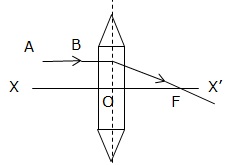
(iv)The point F is called as Focal point or focus.
Solution D.11
(i)The combination forms concave lens.
(ii)XX' is known as principal axis.
(iii)Complete diagram is drawn as
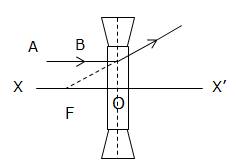
(iv)The point F is called as Focal point or focus.
Solution D.12
(a)
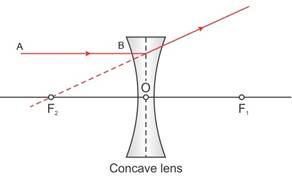
(b)
Solution D.13
(a)
(b)
Refraction Through A Lens Exercise Ex. 5B
Solution A.1
(d) appears to come from the second focus
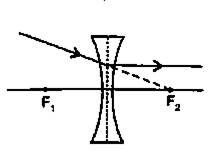
A ray of light parallel to the principal axis for a concave lens after refraction.
Solution A.2
(a)
The above figure represents the correct ray diagram.
Solution A.3
(b) A virtual image can be obtained on the screen.
Only real images can be obtained on screen.
Solution A.4
(d) terrestrial telescope
The erecting lens (convex lens) acts like a second converging lens, introducing another image inversion. This effectively flips the previously inverted image formed by the objective lens, resulting in a final upright and magnified virtual image for the observer to see through the eyepiece.
Solution A.5
(b) 10 cm.
Given that,
Object distance = image distance (∴ the object must be kept at 2f).
2f = 20 cm
∴ f = 10 cm
The focal length of the convex lens is 10 cm.
Solution A.6
(c) Virtual and enlarged.
Explanation: When the object is kept between optical centre and focus of a convex lens, the image is formed on the same side, behind the object.
The image thus formed is virtual, enlarged and erect.
Solution A.7
(b) Virtual, upright and diminished
Hint: Concave lens forms virtual, upright and diminished image for all positions of the object.
Solution A.8
(b) 2F2
Solution A.9
(d) in Galilean telescope
In a Galilean telescope, the concave eyepiece lens makes light rays parallel to those emerging from the objective lens, resulting in a wider field of view but no magnification.
Solution A.10
(d) midpoint between the optical centre and second focus of the lens
For a concave lens, when the object is at a distance equal to the focal length of the lens, the image is formed at the midpoint between the optical centre and second focus of the lens.
Solution B.1
(a) This is convex lens.
(b) The nature of the image is real.
Solution B.2
(a)Concave lens
(b)Image is diminished
Solution B.3
A concave lens cannot form an image two times that of the object because it always forms a diminished image.
Solution B.4
Image formed by a concave lens is virtual and diminished.
Solution B.5
The virtual image formed by a convex lens will be magnified and upright.
Solution B.6
(a)An object is placed at a distance of more than 40 cm from a convex lens of focal length 20 cm. The image formed is real, inverted and diminished.
(b)An object is placed at a distance 2f from a convex lens of focal length f. The image formed is equal to that of the object.
(c)An object is placed at a distance 5 cm from a convex lens of focal length 10 cm. The image formed is virtual, upright and magnified.
Solution B.7
(a)False
(b)False
(c)False
(d)True
(e)False
Solution B.8
If the point source of light is placed at the 'first focal point' (i.e. the focal point on the left of the optical centreof the convex lens), then the rays of light after being refracted through the length obtain a parallel beam of light.
Solution C.1
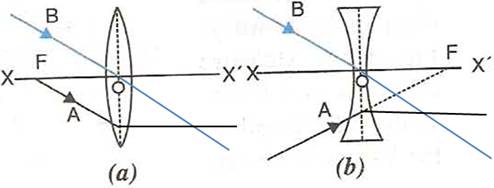
(i)A ray of light incident at the optical centre O of the lens passes undeviated through the lens.
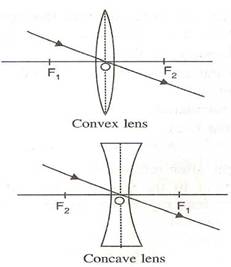
(ii)A ray of light incident parallel to the principal axis of the lens, after refraction passes through the second focus F2 (in a convex lens) or appears to come from the second focus F2 (in a concave lens).
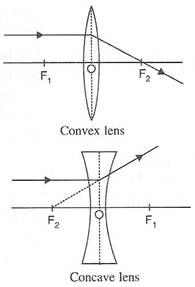
(iii)A ray of light passing through the first focus F1 (in a convex lens) or directed towards the first focus F1 (in a concave lens), emerges parallel to the principal axis after refraction.
Solution C.2
Solution C.3
|
Real image |
Virtual image |
|
1.A real image is formed due to actual intersection of refracted (or reflected) rays. |
1A virtual image is formed when the refracted (or reflected) rays meet if they are produced backwards. |
|
2A real image can be obtained on a screen. |
2.A virtual image can not be obtained on a screen. |
|
3.A real image is inverted with respect to the object. |
3.A virtual image is erect with respect to the object. |
Solution C.4
(a)Convex lens.
(b)Virtual.
Solution C.5
(a)at focus,
(b)at 2F,
(c)between F and 2F,
(d)between optical centre and focus.
Solution C.6
|
Type of lens |
Position of object |
Nature of image |
Size of image |
|
Convex
|
Between optic centre and focus
|
Virtual and upright
|
Magnified
|
|
Convex
|
At focus
|
Real and inverted
|
Very much magnified
|
|
Concave
|
At infinity
|
Virtual and upright
|
Highly diminished |
|
Concave |
At any distance |
Virtual and upright |
Diminished
|
Solution D.1
(a) LL' lens is convex lens.
(b) O and O' are known as first and second focal points respectively.
(c)
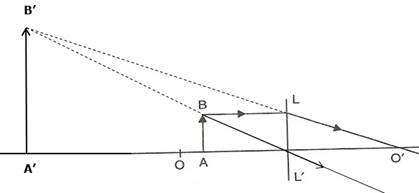
(d) The image formed will be magnified, virtual and upright.
(e) Such action of lens is used in a magnifying glass.
Solution D.2
(i) LL' is concave lens.
(ii)The points O and O' are called second and first focal points respectively.
(iii)

(iv)The three characteristics of the image are :
Virtual
Erect
Diminished
Solution D.3
(a)The complete diagram is

(b)The image formed will be magnified, virtual and upright.
Solution D.4
(i)
(ii) The position of the images will be more than twice the focal length of lens.
(iii) The image will be magnified, real and inverted.
(iv) As the object move towards F1 the image will shift away from F2 and it is magnified. At F1 the image will form at infinity and it is highly magnified. Between F1 and optical centre, the image will form on the same side of object and will be magnified.
Solution D.5
(a) The object is placed beyond 2F1.
(b)
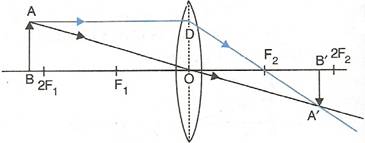
(c) The image is formed beyond 2F2.
(d) The image will be diminished, real and inverted.
Solution D.6
(a) The object is placed at the centre of curvature.
(b)
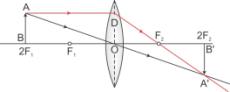
(c) The image formed is real and inverted.
Solution D.7
(a) Convex lens
(b) The object is placed between the lens and focus (F1).
(c)
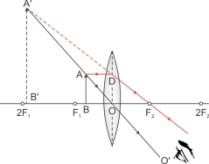
(d) 'Magnifying glass' uses this principle.
Solution D.8
(a) The lens that forms the image between the object and itself is a concave lens.
(b) Ray diagram:
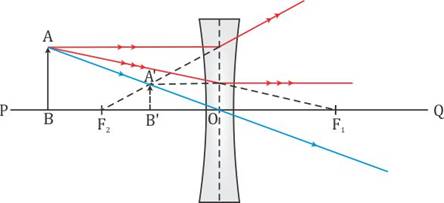
(c) The image formed is virtual, erect and diminished.
Solution D.9
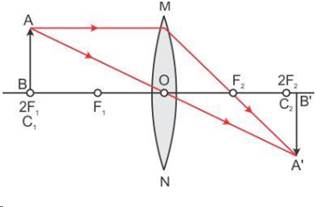
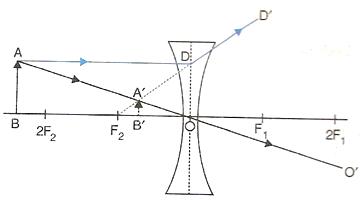
Let the candle is placed beyond 2F1 and its diminished image which is real and inverted is formed between F2 and 2F2.
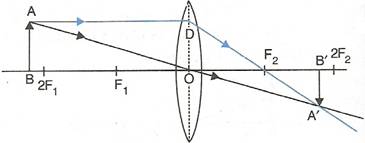
Here the candle is AB and its real and inverted image is formed between F2 and 2F2.
Solution D.10
Solution D.11
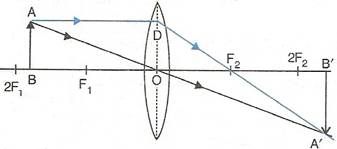
The image formed in above diagram is real, enlarged and inverted.
Solution D.12
If a lens forms an upright and diminished image of an object placed at its focal point, then it is a concave lens.
Solution D.13
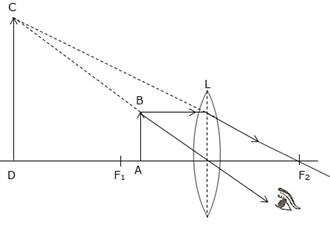
The object is placed between focal point F1 and convex lens and its image is formed at the same side of the lens which is enlarged.
So this lens can be used as a magnifying lens.
Solution D.14
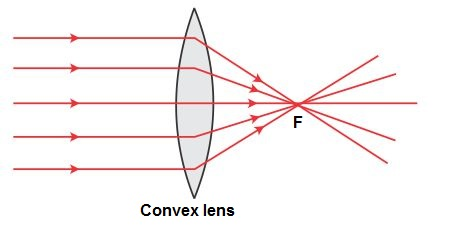
The sun is at infinity so convex lens forms its image at second focal point which is real and very much diminished in size.
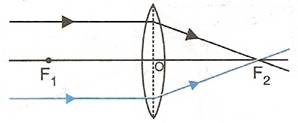
While using the convex lens as burning glass, the rays of light from the sun (at infinity) are brought to focus on a piece of paper kept at the second focal plane of the lens. Due to sufficient heat of the sun rays, the paper burns. Hence this lens is termed as 'burning glass'.
Solution D.15
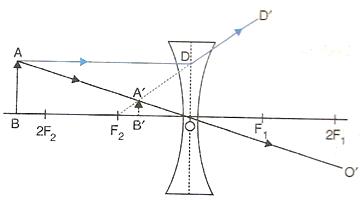
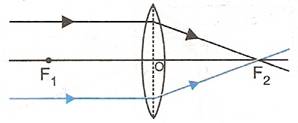
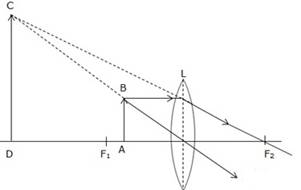
(i)When the object is situated at infinity, the position of image is at F2, it is very much diminished in size and it is real and inverted.
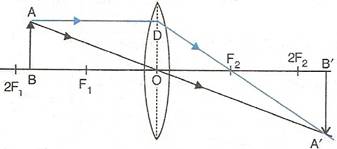
(ii)When the object (AB) is situated beyond 2F1, the position of image (A'B') is between F2 and 2F2, it is diminished in size and real and inverted.
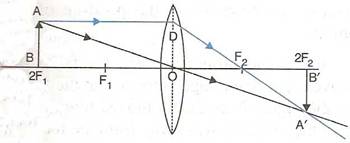
(iii)When the object (AB) is situated at 2F1, the position of image (A'B') is at 2F2, it is of same size as the object and real and inverted.
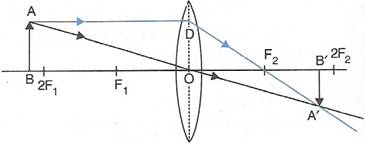
(iv)When the object (AB) is situated between 2F1and F1, the position of image (A'B') is beyond 2F2, it is magnified in size and real and inverted.
(v)When the object (AB) is situated at F1, the position of image is at infinity; it is very much magnified in size and real and inverted.

(vi)When the object (AB) is situated between lens and F1, the position of image (CD) is on the same side, behind the object; it is magnified in size and virtual and upright.
Solution D.16
(i)When object (AB) is situated at infinity then parallel rays from object appears to fall on concave lens. Due to which image forms at focus. This image is highly diminished in size and virtual and upright.
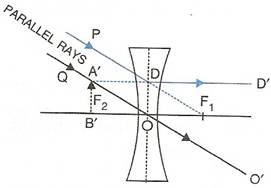
(ii)When object (AB) is situated at any point between infinity and optical centre of the lens then image forms between focus and optical centre. This image is diminished in size and virtual and upright.
Refraction Through A Lens Exercise Ex. 5C
Solution A.1
The correct lens formula is given by option (c).
![]()
According to lens formula we know that,
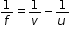
Solution A.2
(c) both positive as well as negative
For a convex lens, the value of magnification m can either be positive or negative. When the image formed is real and inverted the magnification is negative, and if the image formed is erect and virtual, then the magnification is positive.
Solution A.3
(d) the image is real and diminished
If the magnification produced by a lens is - 0.5, the correct statement is real and diminished.
The value of magnification is less than 1, which means that the image formed is diminished.
The negative sign indicates that the image formed is real and inverted.
Also, a convex lens, unlike a concave lens, forms real and inverted images.
Solution A.4
(d) The images is real and diminished formed by a convex
Given that, Magnification is -0.5.
The negative sign of magnification indicates that the image is real while 0.5 indicates that the image is diminished.
A convex lens only forms a real and diminished image of an object.
Solution A.5
b) less than 1
Magnification power for:
convex lens >1
Concave lens <1
Plane mirror = 1
Thus, the numerical value of magnification m is always less than 1 for a concave lens.
Solution A.6
(d) positive, negative
If a lens deviates a ray towards its centre, its power is positive; if it deviates away from its centre, its power is negative.
Solution A.7
(b) Increases
Hint:
![]()
i.e., P ∝ 1/f
Hence when focal length is reduced the power of lens will increase.
Solution A.8
b. convex of focal length 1.0 m
Power of a lens is +1.0 D. The positive sign indicates that the focal length of the lens is positive which indicates the lens is a convex lens.
![]()
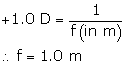
Hence, the correct answer is option (b).
Solution A.9
(c) m = v/u
Linear magnification m is given by,
m = v/u
Solution A.10
(d) -5D
The focal length of the concave lens is negative.
Also, we know,
P = 1/f (in metres) = 1/( – 0.2) = – 5D
Solution B.1
(i) The positive focal length of a lens indicates that it is a convex lens.
(ii) The negative focal length of a lens indicates that it is a concave lens.
Solution B.2
(i) Positive sign of magnification indicates that the image is virtual while negative sign indicates that the image is real.
(ii) Positive sign of magnification indicates that the image is erect while negative sign indicates that the image is inverted.
Solution B.3
![]()
Solution B.4
If focal length of a lens doubled then its power gets halved.
Solution B.5
The sign of power depends on the direction in which a light ray is deviated by the lens. The power could be positive or negative. If a lens deviates a ray towards its centre (converges), the power is positive and if it deviates the ray away from its centre (diverges), the power is negative.
Solution B.6
It is a concave.
Solution B.7
A thick lens has more power than a thin lens. This is because a thick lens has a larger surface curvature. It has a short focal lengthand that is why it deviates the rays of light at a greater extent.
Solution C.1
- The axis along which the distances are measured is called as the principal axis. These distances are measured from the optical centre of the lens.
- All the distances which are measured along the direction of the incident ray of the light are taken positive, while the distances opposite to the direction of the incident ray are taken as negative.
- All the lengths that are measured above the principal axis are taken positive, while the length below the principal axis is considered negative.
- The focal length of the convex lens is taken positive and that of concave lens is negative.
Solution C.2
Lens formula:
![]()
The distance of the object from the optical centre is called the object distance (u).
The distance of the image from the optical centre is called the image distance (v).
The distance of the principal focus from the optical centre is called the focal length (f).
Solution C.3
The term magnification means a comparison between the size of the image formed by a lens with respect to the size of the object.
For a lens: Magnification 'm' is the ratio of the height of the image to the height of the object.

Solution C.4
The power of a lens is a measure of deviation produced by it in the path of rays refracted through it.
Its unit is Dioptre (D).
Solution C.5
The path of ray passing through each convex and concave lens are as shown below:
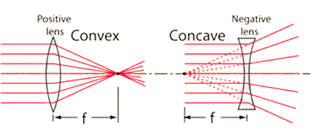
Now, for the given case we have a convex lens of power +2.5 D and a concave lens of power -2.5 D.
When both of them are kept in contact the combined power of lens will be
P = + 2.5 + (-2.5) = 0 D
It means when two lenses of equal and opposite powers are kept in contact, the combination behaves like a plane glass sheet.
Thus, the ray of light passing through the lens combination will continue to travel in a straight line without any deviation.
Solution D.1
Height of the candle (object) = 3 cm
Height of the image of the candle = 6 cm
Image distance = 30 cm
(a) The formula for magnification of a lens is
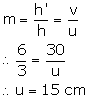
(b) Lens formula is

Solution D.2
Object distance, u = -20 cm
Image distance, v = -10 cm
(a) The image is formed on the same side as the object. Hence, it is a virtual image. Also, since the lens is a concave lens the image will be erect and diminished.
(b) Lens formula is
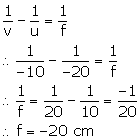
Solution D.3
Focal length, f = +25 cm
Image is virtual and magnified, m = +2
For a lens, magnification is
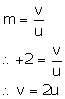
Lens formula is,
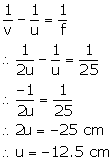
Solution D.4
Focal length of a convex lens, f = +0.12 m
m = -3 (real image)
For a lens, magnification is
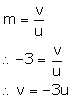
Lens formula is,
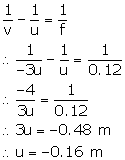
Solution D.5
Image distance, v = 75 cm
Object distance, u = -25 cm
Lens formula is,
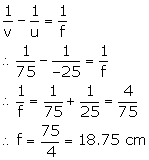
For a lens, magnification is
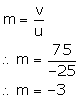
Solution D.6
Object distance, u = -15 cm
Image distance, v = -60 cm
(i) Lens formula is,

(ii) For a lens, magnification is
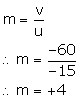
(iii) The nature of the image is erect, virtual and magnified.
Solution D.7
Object distance, u = -45 cm
Image distance, v = +90 cm
(a) As the image is formed on the other side of the lens, the image is real. Hence, the lens is a convex lens.
(b) (i) Lens formula is,
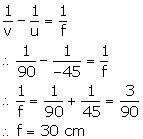
(ii) For a lens, magnification is
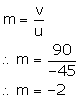
Solution D.8
Object distance, u = -20 cm
Focal length, f = -20 cm (concave lens)
(a) Lens formula is,
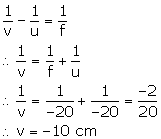
Hence, the image is 10 cm in front of the lens on the same side as the object.
(ii) For a lens, magnification is

Solution D.9
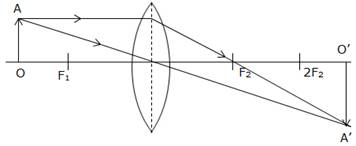
A convex lens forms an inverted, real and an image of the same size as the object when the object is placed at 2f, i.e. (u=2f).
(a)
In such cases, the image is formed at the point which is double the focal length on the other side of the lens (2f2).
(b)
To find the focal length of this lens, we use the relationship:
object distance (u) = 2f
object distance = 60 cm …(given)
60 = 2f
f = 30 cm
So, the focal length of this lens is 30 cm.
Solution D.10
(a)
Given that the concave lens forms an erect image of 1/3rd size of the object.
That implies that the magnification provided by the lens is 1/3.
Magnification is given by
The position of the image formed is 10 cm on the same side of the lens where the object is placed.
(b)
Focal length of a lens is given by
The focal length of the given lens is 15 cm.
Solution D.11
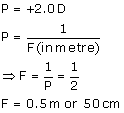
Because the power of the lens is positive, it will be convex lens.
Solution D.12

Solution D.13
Focal length, f = +25 cm = +0.25 m
Power of a lens is
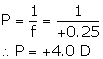
Solution D.14
We know that power of a lens is given by the formula
As the power of the given lens is negative, i.e. -2.0 D, it is a concave lens.
Solution D.15
The negative value of magnification suggests that image is real and inverted. The magnitude of magnification is greater than 1 which means image is enlarged. Therefore the lens should be convex lens.
Relation between u and v is given by

This shows that image distance is 3 times that of object distance.
Solution D.16
The image formed by the concave lens is always virtual, erect and smaller than the object. Therefore the magnification is always positive and less than 1.
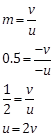
This shows that object distance is twice of image distance.
Solution D.17
Object distance=-30cm
Focal length=f=-3-cm
Image distance=v=?


Here image formed is virtual and erect.
Solution D.18
Object distance=u=-8cm
Focal length f=10cm
Image distance v=?
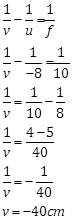
As the object is placed between the focus and optical center of the lens the image formed is virtual and erect.
m = v/u
u = - 8 cm
v = -40 cm
m = - 40/- 8
m = 5
Thus, magnification is + 5
As magnification is positive image formed is erect.
Refraction Through A Lens Exercise Ex. 5D
Solution A.1
(b) 25 cm
The least distance of distinct vision of normal eye is 25 cm.
Solution A.2
(c) A virtual and magnified image
Hint: A magnifying glass forms a virtual, magnified and upright image on the same side as the object.
Solution A.3
(d) 6
Focal length of convex lens, f = +5 cm
Magnifying power of convex lens (simple microscope) is
![]()
D is the distance of distinct vision, D = 25 cm
![]()
Solution A.4
(b) less than 1'
The human eye is not able to see an object distinctly if it subtends an angle less than 1'.
Solution A.5
(a) convex lens of short focal length
A simple microscope uses a convex lens of short focal length.
Solution A.6
Magnifying power of a microscope is given as,
M = 1 + D/f
Where,
M -> magnifying power
D -> least distance of distinct vision
F -> focal length of lens
Solution A.7
(d) convex, concave
Long – sightedness (hypermetropia) is corrected by the convex lens and short-sightedness (myopia) is corrected by the concave lens.
Solution  A.8
(d) A → convex, B → concave
A will be a convex lens as the printed page letters get magnified. The image formed by the convex lens is magnified when an object is placed between the focus and the optical centre. The image formed by lens B is virtual/upright, erect, and diminished for a distant object. Thus, lens B is a concave lens.
Solution B.1
Magnifying glass is a convex lens of short focal length. It is mounted in a lens holder for practical use.
It is used to see and read the small letters and figures. It is used by watch makers to see the small parts and screws of the watch.
Solution B.2
The object is placed between the lens and principal focus.
The image is obtained between the lens and principal focus.
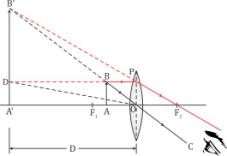
Solution B.3
The magnifying power of the microscope is defined as the ratio of the angle subtended by the image at the eye to the angle subtended by the object (assumed to be placed at the least distance of distinct vision D = 25 cm) at the eye, i.e.,
![]()
where F is the focal length of the lens.
The magnifying power of a microscope can be increased by using the lens of short focal length. But it cannot be increased indefinitely.
Solution B.4
The two applications of a convex lens are:-
(i)It is used as an objective lens in a telescope, camera, slide projector, etc.
(ii)With its short focal length it is also used as a magnifying glass.
The two applications of a concave lens are:-
(i)A person suffering from short sightedness or myopia wears spectacles having concave lens.
(ii)A concave lens is used as eye lens in a Galilean telescope to obtain an erect final image of the object.
Solution B.5
(i) On seeing a distant object through the lens, if its inverted image is seen, then the lens is convex, and if the upright image is seen, then the lens is concave.
(ii) On keeping the lens near a printed page, if the letters appear magnified, then the lens is convex, and if the letters appear diminished, then the lens is concave.
Solution C.1
Let the object (AB) is situated between focal length and optical centre of a convex lens then its image (A'B') will form on the same side of lens.
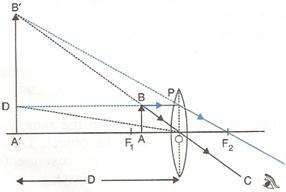
The image formed will be virtual, magnified and erect.
Solution C.2
The approximate focal length of a convex lens can be determined by using the principle that a beam of parallel rays incident from a distant object is converged in the focal plane of the lens.
In an open space, against a white wall, a metre scale is placed horizontally with its 0 cm end touching the wall.
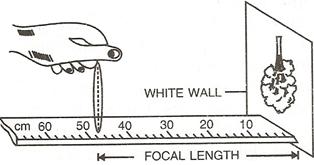
By moving the convex lens to and fro along the scale, focus a distant object on wall. The image which forms on the wall is very near to the focus of the lens and the distance of the lens from the image is read directly by the metre scale. This gives the approximate focal length of the lens.
Solution C.3
(i)
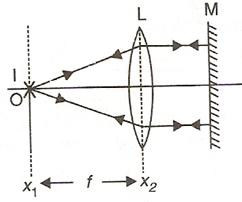
(ii)The size of the image will be same as that of object.
(iii)The image formed will be real and inverted.
(iv)The distance of object O from optical lens will be equal to the focal length of the lens.
(v)The position of the mirror from lens does not affect the formation of image as long as the rays from the lens fall normally on the plane mirror M.
Solution C.4
To determine focal length by using plane mirror we need a vertical stand, a plane mirror, a lens and a pin.
Place the lens L on a plane mirror MM' horizontally. Arrange a pin P on the clamp of a vertical stand such that the tip of pin is vertically above the centre O of the lens.

Adjust the height of the pin until it has no parallax (i.e., when the pin and its image shift together) with its inverted image as seen from vertically above the pin.
Now measure the distance x of the pin from the lens and the distance y of the pin from the mirror, using a metre scale and a plumb line. Calculate the average of the two distances. This gives the focal length of the lens, i.e.,
![]()