Class 10 SELINA Solutions Physics Chapter 1 - Force
Force Exercise Ex. 1A
Solution A.1
(a) ![]() (mass m is constant)
(mass m is constant)
The mathematical expression of Newton's second law of motion is as shown below:
Force = Mass × Acceleration
i.e., Force ∝ Acceleration.
Solution A.2
(c) linear motion
The body moves along a straight line is said be in a linear motion.
Solution A.3
(a) rotational motion
When the body is pivoted at a point and force is applied to it at a suitable point, rotational motion is produced.
Solution A.4
(d) Both on the force and its perpendicular distance from the axis.
The moment of a force about a given axis depends on both on the force and its perpendicular distance from the axis.
Hint: Moment of force = Force x Perpendicular distance
Solution A.5
(c) maximum
The moment of force is equal to the product of the magnitude of the force and the perpendicular distance of the line of action of force from the axis of rotation.
i.e., Moment of force about a given axis= Force × perpendicular distance of force from the axis of rotation.
Thus, for a given force to produce the maximum turning effect on a body, the perpendicular distance of the line of action of force from the axis of rotation should be maximum.
Solution A.6
(a) 1
The moment of force is equal to the product of the magnitude of the force and the perpendicular distance of the line of action of force from the axis of rotation.
S.I. unit of moment of force is Newton metre (Nm).
Whereas the C.G.S. unit of moment of force is Dyne cm (dyn cm)
The relation be S.I. and C.G.S. units of moment of force are:
1 Nm = 107 dyne cm
Thus, 107 dyne cm is equal to 1 Nm.
Solution A.7
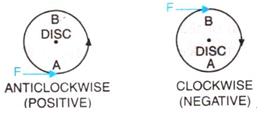
(a) positive, negative
As we know, the moment of force for the anticlockwise moment is taken as positive, and for the clockwise moment, it is taken as negative.
Solution A.8
(c) both the direction of force and the point of application of force
The moment of force is equal to the product of the magnitude of the force and the perpendicular distance of the line of action of force from the axis of rotation.
Hence, the direction of rotation of a pivoted body can be changed by changing both the direction of force and the point of application of force.
Solution A.9
(c) two equal and opposite parallel forces
A couple is formed when two equal and opposite parallel forces are not acting along the same line.
Solution A.10
(b) Sum of anticlockwise moments is equal to sum of clockwise moments.
According to the principle of moments in equilibrium, the sum of anticlockwise moments is equal to the sum of clockwise moments.
Solution A.11
(d) the body will have both rotational as well as translational motion
Since the two forces are unequal and along opposite directions, the effect will cause the body to have both rotational as well as translational motion.
Solution A.12
(b) (1), (2) and (3)
A body is in static equilibrium when it remains resting under applied forces, while in dynamic equilibrium, it remains in the same state of motion.
Hence, “A beam balance balanced in a horizontal position” is an example of static equilibrium, whereas the rest are examples of dynamic equilibrium.
Solution B.1
(a)When the body is free to move it produces translational motion.
(b)When the body is pivoted at a point, it produces rotational motion.
Solution B.2
Moment of a force is a vector.
Solution B.3
Moment of force about a given axis = Force x perpendicular distance of force from the axis of rotation.
Solution B.4
Moment of force depends on the distance of line of action of the force from the axis of rotation. Decreasing the perpendicular distance from the axis reduces the moment of a given force.
Solution B.5
Moment of a force is the product of the force and the perpendicular distance of force from axis of rotation. So, one way to increase the moment would be to increase the distance from the axis of rotation where the force would act.
Solution B.6
(i) The S.I. unit of moment of force is newton-metre.
(ii) In equilibrium algebraic sum of moments of all forces about the point of rotation is zero.
(iii) In a beam balance when the beam is balanced in a horizontal position, it is in static equilibrium.
(iv) The moon revolving around the earth is in dynamic equilibrium.
Solution C.1
The moment of force is equal to the product of the magnitude of the force and the perpendicular distance of the line of action of force from the axis of rotation.
S.I. unit of moment of force is Newton metre (Nm).
Solution C.2
Moment of force about a point depends on the following two factors:
(a)The magnitude of the force applied and,
(b)The distance of line of action of the force from the axis of rotation.
Solution C.3
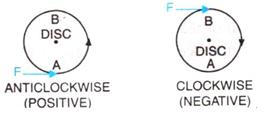
When the body is pivoted at a point, the force applied on the body at a suitable point rotates the body about the axis passing through the pivoted point.
The direction of rotation can be changed by changing the point of application of force. The given figure shows the anticlockwise and clockwise moments produced in a disc pivoted at its centre by changing the point of application of force F from A to B.
Solution C.4
If the turning effect on the body is anticlockwise, moment of force is called anticlockwise moment and it is taken as positive while if the turning effect on the body is clockwise, moment of force is called clockwise moment and is taken negative.
Solution C.5
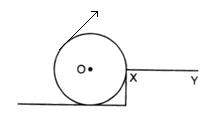
It is easier to open a door by applying the force at the free end of it because larger the perpendicular distance, less is the force needed to turn the body.
Solution C.6
The stone of hand flour grinder is provided with a handle near its rim so that it can be rotated easily about the iron pivot at its centre by a small force applied at the handle.
Solution C.7
It is easier to turn the steering wheel of a large diameter than that of a small diameter because less force is applied on steering of large diameter which is at a large distance from the centre of rim.
Solution C.8
A spanner (or wrench) has a long handle to produce larger turning moment so that nut can easily be turned with a less force.
Solution C.9
A jack screw has a long arm so that less effort is required to rotate it to raise or lower the jack, which is used to lift a heavy load like a vehicle.
Solution C.10
Force F should be provided in the direction as shown in the diagram.
Solution C.11
The moment of a couple is equal to the product of the either force and the perpendicular distance between the line of action of both the forces. S.I unit of moment of couple is Nm.
Solution C.12
When a number of forces acting on a body produce no change in its state of rest or of motion, the body is said to be in equilibrium.
Solution C.13
(i)When a body remains in the state of rest under the influence of the applied forces, the body is in static equilibrium. For example a book lying on a table is in static equilibrium.
(ii)When a body remains in the same state of motion (translational or rotational), under the influence of the applied forces, the body is said to be in dynamic equilibrium. For example, a rain drop reaches the earth with a constant velocity is in dynamic equilibrium.
Solution C.14
For a body to be in equilibrium:
(i)The resultant of all the forces acting on the body should be equal to zero.
(ii)The resultant moment of all the forces acting on the body about the point of rotation should be zero.
Solution C.15
According to the principle of moments, if the algebraic sum of moments of all the forces acting on the body about the axis of rotation is zero, the body is in equilibrium. A physical balance (or beam balance) works on the principle of moments.
Solution D.1

Solution D.2
(a) If both forces of equal magnitude act at the same point of the body,
The resultant force acting on the body = F - F= 0
i.e., moment of forces, τ = 0
Thus, there is no motion of the body
(b) Now, if the two forces act at two different points of the body at a separation r.
The forces tend to rotate the body about the mid-point between two forces,
i.e., Moment of force, τ = Fr
Solution D.3
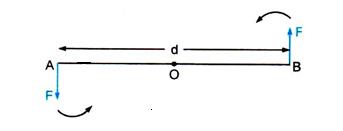
At A and B, two equal and opposite forces each of magnitude F are applied. The two forces rotate the bar in anticlockwise direction.
Solution D.4
Two equal and opposite parallel forces not acting along the same line, form a couple. A couple is always needed to produce the rotation. For example, turning a key in a lock and turning a steering wheel.
Solution D.5
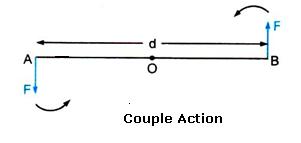
At A and B, two equal and opposite forces each of magnitude F are applied. The two forces rotate the bar in anticlockwise direction. The perpendicular distance between two forces is AB which is called the couple arm.
Moment of force F at the end A
= F x OA(anticlockwise)
Moment of force F at the end B
= F x OB(anticlockwise)
Total moment of couple =F x OA + F x OB
= F x (OA +OB)= F x AB
= F x d(anticlockwise)
=Either force x perpendicular distance between the two forces (or couple arm)
Thus, Moment of couple = Force x Couple arm
Solution D.6
Suspend a metre rule horizontally from a fixed support by means of a strong thread at O as shown. Now suspend two spring balances with some slotted weights W1 and W2 on them on either side of the thread. The scale may tilt to one side. Now adjust the distances of two spring balances from the support by keeping one at A and the other at B in such a way that the scale again becomes horizontal.

Let the weight suspended on the right side of thread from the spring balance at A be W1 at distance OA=l1, while the weight suspended on the left side of thread from the spring balance at B be W2 at distance OB= l2.
The weight W1 tends to turn the scale clockwise, while the weight W2 tend to turn the scale anticlockwise.
Clockwise moment = W1 x l1
Anticlockwise moment = W2 x l2
In equilibrium, when the scale is horizontal, it is found that
Clockwise moment = Anticlockwise moment
i.e.,W1 x l1 = W2 x l2
This verifies the principle of moments.
Solution E.1
Moment of force= force × perpendicular distance of force from point O
Moment of force= F × r
10 Nm = 20 × r
R = 10/20 = 0.5 m
Solution E.2
2.5 N m.
Given that,
Force = 10 N
Distance = 25 cm = 0.25 m
Now,
Moment of force = Force × Distance
Moment of force = 10 × 0.25 = 2.5 N m
Solution E.3
Given , F= 2N
Diameter=2m
Perpendicular distance between B and O =1m
(i)Moment of force at point O
= F x r
=2 x 1=2Nm (clockwise)
(ii)Moment of force at point A= F x r
=2 x 2=4Nm (clockwise)
Solution E.4
Given AO=2m and OB=4m
(i)Moment of force F1(=5N) at A about the point O
=F1 x OA
=5 x 2= 10Nm (anticlockwise)
(ii)Moment of force F2(=3N) at B about the point O
= F2 x OB
=3 x 4=12 Nm(clockwise)
(iii)Total moment of forces about the mid-point O=
= 12- 10=2Nm(clockwise)
Solution E.5
Given, AB=4m hence, OA=2m and OB =2m
Moment of force F(=10N) at A about the point O
= F x OA= 10 x 2= 20Nm (clockwise)
Moment of force F (=10N) at point B about the point O
= F x OB= 10 x 2 =20Nm (clockwise)
Total moment of forces about the mid-point O=
=20 +20= 40Nm(clockwise)
Solution E.6
(i)Perpendicular distance of point A from the force F=10 N at B is 0.5m , while it is zero from the force F=10N at A
Hence, moment of force about A is
= 10 N x 0.5m=5Nm(clockwise)
(ii)Perpendicular distance of point B from the force F=10 N at A is 0.5m, while it is zero from the force F=10N at B
Hence, moment of force about B is
= 10 N x 0.5m=5Nm(clockwise)
(iii)Perpendicular distance of point O from either of the forces F=10N is 0.25 m
Moment of force F(=10N) at A about O= 10N x 0.25m
=2.5Nm(clockwise)
And moment of force F(=10N) at B about O
=10N x 0.25m=2.5Nm(clockwise)
Hence, total moment of the two forces about O
=0.25 + 0.25=5Nm (clockwise)
Solution E.7
Moment of couple = either force × couple arm
= 6 N × 0.5 m
= 3.0 Nm
Solution E.8
Let the 50gf weight produce anticlockwise moment about the middle point of metre rule .i.e, at 50cm.
Let a weight of 100gf produce a clockwise moment about the middle point. Let its distance from the middle be d cm. Then,
according to principle of moments,
Anticlockwise moment = Clockwise moment
50gf x 50 cm=100gf x d
So, d= ![]()
Solution E.9
(i)Weight mg (W) of rule produces an anti-clockwise moment about the knife edge O. In order to balance it, 20gf must be suspended at the end B to produce clockwise moment about the knife edge O.
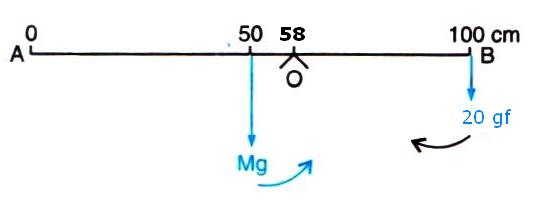
(ii)
From the principle of moments,
Anticlockwise moment= Clockwise moment
Wx (58-50) =20gf x (100-58)
W x 8=20gf x 42
W = ![]()
Solution E.10
Anticlockwise moment= 40gf x 40 cm
Clockwise moment= 80gf x d cm
From the principle of moments,
Anticlockwise moment= Clockwise moment
40gf x 40 cm =80gf x d
So, d = ![]() .
.
Solution E.11
(i)Anticlockwise moment= 40gf x (50-10)cm
=40gf x 40cm=1600 gf x cm
Clockwise moment= 20gf x (90- 50) =20gf x 40cm
=800 gf x cm
Anticlockwise moment is not equal to clockwise moment. Hence the metre rule is not in equilibrium and it will turn anticlockwise.
(ii)To balance it, 40gf weight should be kept on right hand side so as to produce a clockwise moment about the middle point. Let its distance from the middle be d cm. Then,
clockwise moment= 20gf x 40cm + 40gf x d cm
From the principle of moments,
Anticlockwise moment= Clockwise moment
40 gf x 40 cm= 20gf x 40 + 40 x d cm
1600-800=40gf x dcm
So, d= ![]() (on the other side)
(on the other side)
Hence, by placing the additional weight of 40gf at the 70cm mark the rule can be brought in equilibrium.
Solution E.12
From the principle of moments,
Anticlockwise moment= Clockwise moment
20kgf x 2m =40kgf x d
So, d= ![]() from the centre on the side opposite to the boy.
from the centre on the side opposite to the boy.
Solution E.13
From the principle of moments,
Anticlockwise moment= Clockwise moment
100 gf x 40 cm =W x 60 cm
So, weight on the longer pan ,
W=![]()
Solution E.14
(i)Total anticlockwise moment about O
= 150gf x 40 cm=6000gf cm
(ii)Total clockwise moment about O,
=250gf x 20 cm= 5000gf cm
(iii)The difference of anticlockwise and clockwise moment= 6000- 5000= 1000gf cm
(iv)From the principle of moments,
Anticlockwise moment= Clockwise moment
To balance it, 100gf weight should be kept on right hand side so as to produce a clockwise moment about the O. Let its distance from the point O be d cm. Then,
150gf x 40 cm=250gf x 20 cm +100gf x d
6000gf cm= 5000gf cm + 100gf x d
1000gf cm =100 gf x d
So, d=![]() on the right side of O.
on the right side of O.
Solution E.15
(i)Anticlockwise moment= 10gf x 50 cm= 500gf cm
(ii)From the principle of moments,
Anticlockwise moment= Clockwise moment
10gf x 50 cm= W x 100cm
So, W= ![]()
By applying a force 5gf upwards at the 100cm mark, rule can be made horizontal
Solution E.16
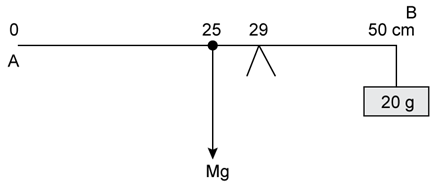
Figure shows a uniform half metre rule PQ which is balanced at 29cm mark. Let M be the mass of the rule. A uniform rule has same distribution of mass throughout its length So its weight Mg will act at its middle point which is at 25cm. The weight mg produces anticlockwise moment about point o. In order to balance the 20g (0.02kg) weight is tied at 50cm mark which generates clockwise moment.
Hence from the principle of moments
Anticlockwise moment= clockwise moment
Mg(29-25)=0.02g(50-29)
M=21(0.02)/4
M=0.105kg
M=105g
Solution E.17
(i) From the principle of moments,
Clockwise moment= Anticlockwise moment
100g x (50-40) cm= mx(40-20) cm
100g x 10 cm = m x 20 cm = m =50 g
(ii)The rule will tilt on the side of mass m (anticlockwise), if the mass m is moved to the mark 10cm.
(iii)Anticlockwise moment if mass m is moved to the mark 10 cm= 50g x (40-10)cm =50 x 30=1500g cm
Clockwise moment=100g x (50-40) cm= 1000g cm
Resultant moment= 1500g cm -1000g cm= 500g cm (anticlockwise)
(iv) From the principle of moments,
Clockwise moment= Anticlockwise moment
To balance it, 50g weight should be kept on right hand side so as to produce a clockwise moment .Let its distance from fulcrum be d cm. Then,
100g x (50-40) cm + 50g x d =50g x (40-10)cm
1000g cm + 50g x d =1500 g cm
50 g x d= 500g cm
So, d =10 cm
By suspending the mass 50g at the mark 50 cm, it can be balanced.
Solution E.18
According to the principle of moments,
Clockwise moments = anticlockwise moments
![]()
As the system is in equilibrium,

Force Exercise Ex. 1B
Solution A.1
(d) All of the above
A body's centre of gravity (C.G.) is the point where the algebraic sum of moments of weights of all the particles constituting the body is zero.
Thus, the following statements about the centre of gravity are correct:
1) The position of the centre of gravity of a body of a given mass depends on its shape.
2) The centre of gravity doesn't need to always be within the material of the body.
3) By the centre of gravity concept, a body of weight W can be considered as a point particle of weight W at its centre of gravity.
Solution A.2
(d) 0
The centre of gravity of a body is the point about which the algebraic sum of moments of weights of all the particles constituting the body is zero.
Solution A.3
(a) At its geometrical centre
As ball is uniform and it is a regular body centre of gravity will be situated at its centre that is it will be situated at its geometric centre.
Solution A.4
(c) 2h/3.
The centre of gravity of a hollow cone is at a height h/3 from the base. Hence, from the vertex the height is h - h/3 = 2h/3.
Solution A.5
(d) both (a) and (b)
For the stable equilibrium of a body, its centre of gravity must be as low as possible. It must be above the base and near the geometric centre of the body.
Solution A.6
(b) the one with a smaller base
As we know, an object's centre of gravity is determined by mass distribution. In our case, the mass of both objects is the same, but their shapes are different. Thus, the centre of gravity of an object, which is easier to topple, will be higher.
This is because the centre of gravity is the point at which the object's entire weight acts, and with a smaller base, the weight is concentrated closer to the top, raising the centre of gravity.
Hence, objects with small bases will have a higher centre of gravity.
Solution B.1
Yes, the centre of gravity can be situated outside the material of the body. For example, centre of gravity of ring.
Solution B.2
The position of centre of gravity of a
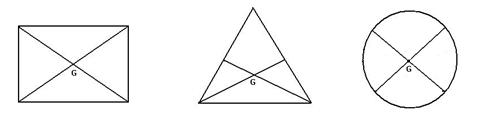
(a) rectangular lamina is at the point of intersection of its diagonals.
(b) cylinder is at the mid point on the axis of cylinder.
Solution B.3
(a)Centre of gravity of a triangular lamina is situated at the point of intersection of its medians.
(b)Centre of gravity of a circular lamina is situated at the centre of circular lamina.
Solution B.4
Centre of gravity of a uniform ring is situated at the centre of ring.
Solution B.5
(i) False. The position of centre of gravity of a body of given mass depends on its shape i.e., on the distribution of mass in it.
(ii) True.
Solution C.1
Centre of gravity is the point about which the algebraic sum of moments of weights of particles constituting the body is zero and the entire weight of the body is considered to act at this point.
Solution C.2
The position of centre of gravity of a body of given mass depends on its shape i.e., on the distribution of mass in it. For example: the centre of gravity of a uniform wire is at its mid-point. But if this wire is bent into the form of a circle, its centre of gravity will then be at the centre of circle.
Solution C.3
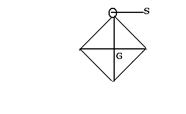
A square card board in rest position with G as centre of gravity and S as point of suspension.
Solution C.4
Solution C.5
Solution D.1
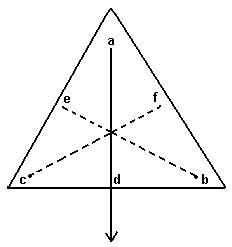
Take a triangular lamina. Make three fine holes at a, b, c near the edge of triangular lamina. Now suspend the given lamina along with a plumb line from hole 'a'. Check that the lamina is free to oscillate about the point of suspension. When lamina has come to rest, draw straight line ad along the plumb line. Repeat the experiment by suspending the lamina through hole 'b' and then through hole 'c' for which we get straight lines be and cf respectively. It is noticed that the lines ad, be and cf intersect each other at a common point G which is the position of centre of gravity of triangular lamina i.e. the point of intersection of medians.
Force Exercise Ex. 1C
Solution A.1
(b) Speed
Hint: Speed is scalar, but velocity and acceleration are vector quantities. So, speed remains constant, but velocity and acceleration change with the change in direction, and in circular motion the direction of motion changes at every point.
Solution A.2
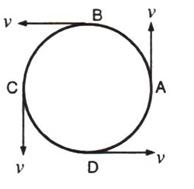
(b) is along with tangent at that point of the circular path.
At point in circular motion, the direction of motion will be along the tangent drawn at the point of the circular path.
Solution A.3
(b) A centripetal force is defined as the force acting on a body moving in a circular path, in a direction toward the centre of the circular path.
Solution A.4
(c) a fictitious force
The centrifugal force is a fictitious force.
Solution A.5
(b) they both act in opposite directions
A centripetal force acts a direction toward the centre of the circular path.
Whereas a centrifugal force acts in a direction away from the centre of circular path.
Solution A.6
(c) a satellite orbiting the Earth at a constant altitude.
When a particle moves with a constant speed in a circular path, its motion is said to be the uniform circular motion.
Hence, a satellite orbiting the Earth at a constant altitude is an example of uniform circular motion.
Solution B.1
Yes, uniform circular motion has an accelerated motion with a constant speed.
Solution B.2
Motion of a cyclist on a circular track is an example of motion in which speed remains uniform, but the velocity changes.
Solution B.3
Centripetal force is required for circular motion. It is always directed towards the centre of circle.
Solution B.4
No, centrifugal force is a fictitious force.
Solution B.5
(a)False
(b)True
(c)True
(d)False
(e)False
Solution C.1
|
Uniform linear motion |
Uniform circular motion |
|
The body moves along a straight line. |
The body moves along a circular path. |
|
Speed and direction both remain constant. |
Speed is constant, but direction changes continuously. |
|
It is not an accelerated motion. |
It is an accelerated motion. |
Solution C.2
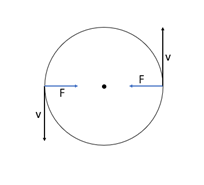
Force acting on a body which is in circular motion is called centripetal force. It acts towards the centre of circular path.
Solution C.3
A planet moves around the sun in a nearly circular path for which the gravitational force of attraction on the planet by the sun provides the necessary centripetal force required for circular motion.
Solution C.4
(a) They act in opposite directions.
(b) No, centrifugal force is not the force of reaction of centripetal force.
(c) The magnitudes of centripetal and centrifugal force will be equal but opposite in direction.
i.e., Ratio of magnitude of centripetal and centrifugal force = 1:1
Solution C.5
|
Centripetal force |
Centrifugal force |
|
It acts towards the centre of the circle. |
It acts away from the centre of the circle. |
|
It is a real force. |
It is a fictitious force. |
Solution D.1
When a particle moves with a constant speed in a circular path, its motion is said to be the uniform circular motion. For example : Revolution of earth around sun is an example of uniform circular motion.
Solution D.2
Particle moving in a circular path with a constant speed.
Solution D.3
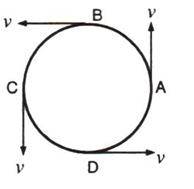
When the object moves in a circular path with uniform speed, it means that its magnitude of velocity does not change, only its direction changes continuously.
Hence, it is considered as uniformly accelerated motion.
Solution D.4
a. On standing outside the disc, we find that the pebble is moving on a circular path. On standing at the centre of the disc, we find that the pebble is stationary placed just in front of us.
b. The pebble is stationary just in front because the centrifugal force on the pebble balances the tension in the string.
Solution D.5
(a) Velocity of stone will be variable
(b) Acceleration of stone will be variable
(c) Direction of acceleration of stone at any instance will be towards the centre of the circular path
(d) The tension in the thread provides the centripetal force required for circular motion.
(e) The force that acts on the hand is the reaction force to the tension in the thread and its direction is opposite to that of the tension in the thread.