Class 10 SELINA Solutions Physics Chapter 11 - Calorimetry
Calorimetry Exercise Ex. 11A
Solution A.1
(c) thermal energy
The total internal energy of all molecules of a substance is called thermal energy.
Solution A.2
(d) Both (b) and (c)
The S.I. unit of heat is Joule (J), and the other most commonly used unit of heat is calorie (cal).
Solution A.3
(b) J K-1
The S.I. unit of heat capacity is joule per kelvin (J K-1).
Solution A.4
(b) J K-1
Solution A.5
(c) J kg-1 K-1
Solution A.6
(a) 4200 J kg-1 K-1
Solution A.7
(b) Tk = 273 + t °C
By adding 273 (≈ 273.15) to the temperature in degrees Celsius, we get the temperature in Kelvin.
Solution A.8
(d) All of the above
The amount of heat energy contained in a body depends on:
1. The mass of the body
2. The increase in temperature of the body,
3. The material of the body
Solution A.9
(b) Q= mcΔt
The amount of heat energy contained in a body depends on its mass, temperature and the material of body.
i.e., Q ∝ mΔt ⇒ Q = mΔt
Solution A.10
(a) C’ = m ×c
Heat capacity C’ = mass m× specific heat capacity c
Solution A.11
(a) low, high
A good conductor of heat has a low specific heat capacity, while a bad conductor has a high specific heat capacity.
Solution A.12
(d) hydrogen
For the given case, the lowest specific heat capacity is hydrogen.
Solution A.13
(c) both (a) and (b)
According to the principle of calorimetry, the heat energy lost by the hot body is equal to the heat energy gained by the cold body.
This is based on the law of conservation of heat and energy.
Solution A.14
(c) principle of calorimetry
The principle of calorimetry is used to measure heat.
Solution B.1
S.I. unit of heat is joule (symbol J).
Solution B.2
Heat capacity = Mass x specific heat capacity
Solution B.3
Water has the highest specific heat capacity.
Solution B.4
Specific heat capacity of water=4200 J kg-1 K-1.
Solution B.5
The expression for the heat energy Q
Q= mc![]() t (in joule)
t (in joule)
Solution B.6
Heat capacity of liquid A is less than that of B.
As the substance with low heat capacity shows greater rise in temperature.
Solution B.7
(i)Radiator in car.
(ii)To avoid freezing of wine and juice bottles.
Solution B.8
The specific heat capacity of liquid X is higher than that of Y. So, for same mass and same heat energy, the rise in temperature for X will be less than that of Y.
(i) As a coolant in car radiators, the liquid needs to absorb more energy without much change in temperature. So, liquid X is ideal for this function.
(ii) As a heat reservoir to keep juice bottles without freezing, the liquid needs to give out large amount of heat before reaching freezing temperatures. Hence, liquid X is ideal for this function.
Solution C.1
The kinetic energy due to random motion of the molecules of a substance is known as its heat energy.
Solution C.2
One calorie of heat is the heat energy required to raise the temperature of 1 g of water from 14.5oC to 15.5 oC.
1 calorie = 4.186 J
Solution C.3
One kilo-calorie of heat is the heat energy required to raise the temperature of 1 kg of water from 14.5oC to 15.5oC.
Solution C.4
The quantity which determines the direction of flow of heat between two bodies kept in contact is called temperature.
S.I. unit kelvin (K).
Solution C.5
|
Heat |
Temperature |
|
The kinetic energy due to random motion of the molecules ofa substance is known as its heat energy. |
The quantity which determines the direction of flow of heat between two bodies kept in contact is called temperature. |
|
S.I. unit joule (J). |
S.I. unit kelvin (K). |
|
It is measured by the principle of calorimetry. |
It is measured by a thermometer. |
Solution C.6
The measurement of the quantity of heat is called calorimetry.
Solution C.7
The heat capacity of a body is the amount of heat energy required to raise its temperature by 1oC or 1K.
S.I. unit is joule per kelvin (JK-1).
Solution C.8
The specific heat capacity of a substance is the amount of heat energy required to raise the temperature of unit mass of that substance through by 1oC (or 1K).
S.I. unit is joule per kilogram per kelvin (Jkg-1K-1).
Solution C.9
Heat capacity of the body is the amount of heat required to raise the temperature of (whole) body by 1![]() whereas specific heat capacity is the amount of heat required to raise the temperature of unit mass of the body by 1
whereas specific heat capacity is the amount of heat required to raise the temperature of unit mass of the body by 1![]() .
.
Heat capacity of a substance depends upon the material and mass of the body. Specific heat capacity of a substance does not depend on the mass of the body.
S.I. unit of heat capacity is![]() and S.I. unit of specific heat capacity is
and S.I. unit of specific heat capacity is![]() .
.
Solution C.10
(i) The heat capacity of a body is 50JK-1 means to increase the temperature of this body by 1K we have to supply 50 joules of energy.
(ii) The specific heat capacity of copper is 0.4Jg-1K-1 means to increase the temperature of one gram of copper by 1K we have to supply 0.4 joules of energy.
Solution C.11
The specific heat capacity of substance B is lesser than that of A. So, for same mass and same heat energy, the rise in temperature for B will be more than that of A. Hence, substance B is a good conductor of heat.
Solution C.12
Change in temperature and the nature of material
Solution C.13
The quantity of heat energy absorbed by a body depends on three factors :
(i)Mass of the body - The amount of heat energy required is directly proportional to the mass of the substance.
(ii)Nature of material of the body - The amount of heat energy required depends on the nature on the substance and it is expressed in terms of its specific heat capacity c.
(iii)Rise in temperature of the body - The amount of heat energy required is directly proportional to the rise in temperature.
Solution C.14

Solution C.15
The principle of method of mixture:
Heat energy lost by the hot body = Heat energy gained by the cold body.
This principle is based on law of conservation of energy.
Solution C.16
In the absence of water, if on a cold winter night the atmospheric temperature falls below 0oC, the water in the fine capillaries of plant will freeze, so the veins will burst due to the increase in the volume of water on freezing. As a result, plants will die and the crop will be destroyed. In order to save the crop on such cold nights, farmers fill their fields with water because water has high specific heat capacity, so it does not allow the temperature in the surrounding area of plants to fall up to 0oC.
Solution C.17
The reason is that water does not cool quickly due to its large specific heat capacity, so a hot water bottle provides heat energy for fomentation for a long time.
Solution C.18
By allowing water to flow in pipes around the heated parts of a machine, heat energy from such part is removed. Water in pipes extracts more heat from surrounding without much rise in its temperature because of its large specific heat capacity. So, Water is used as an effective coolant.
Solution C.19
By making the base of a cooking pan thick, its thermal capacity becomes large and it imparts sufficient heat energy at a low temperature to the food for its proper cooking. Further it keeps the food warm for a long time, after cooking.
Solution D.1
A mass m1 of a substance A of specific heat capacity c1 at temperature T1 is mixed with a mass m2 of other substance B of specific heat capacity c2 at a lower temperature T2 and final temperature of the mixture becomes T.
Fall in temperature of substance A = T1 - T
Rise in temperature of substance B = T – T2
Heat energy lost by A = m1 ![]() c1
c1 ![]() fall in temperature
fall in temperature
= m1c1(T1 - T)
Heat energy gained by B= m2 ![]() c2
c2 ![]() rise in temperature
rise in temperature
= m2c2(T – T2)
If no energy lost in the surrounding, then by the principle of mixtures,
Heat energy lost by A = Heat energy gained by B
m1c1(T1 - T)= m2c2(T – T2)
After rearranging this equation, we get
![]()
Here we have assumed that there is no loss of heat energy.
Solution D.2
The specific heat capacity of water is very high. It is about five times as high as that of sand. Hence the heat energy required for the same rise in temperature by a certain mass of water will be nearly five times than that required by the same mass of sand. Similarly, a certain mass of water will give out nearly five times more heat energy than that given by sand of the same mass for the same fall in temperature. As such, sand gets heated or cooled more rapidly as compared to water under the similar conditions. Thus a large difference in temperature is developed between the land and the sea due to which land and sea breezes are formed. These breezes make the climate near the sea shore moderate.
Solution D.3
(a)A calorimeter is a cylindrical vessel which is used to measure the amount of heat gained or lost by a body when it is mixed with other body.
(b)It is made up of thin copper sheet because:
(i) Copper is a good conductor of heat, so the vessel soon acquires the temperature of its contents.
(ii)Copper has low specific heat capacity so the heat capacity of calorimeter is low and the amount of heat energy taken by the calorimeter from its contents to acquire the temperature of its contents is negligible.
(c)Heat capacity of the calorimeter should be low so out of three metals the one which have lowet specific heat capacity should be preferred.
(d) By polishing the outer and inner surface of the vessel the loss due to radiation can be minimised.
Solution E.1
The size of 1 degree on the Kelvin scale is the same as the size of 1 degree on the Celsius scale. Thus, the difference (or change) in temperature is the same on both the Celsius and Kelvin scales.
Therefore, the corresponding rise in temperature on the Kelvin scale will be 15K.
Solution E.2
Given that,
Mass of copper vessel = 200 g = 0.2 kg
The specific heat capacity of copper = 410 J kg-1 K-1
Change in temperature = (35 - 25) oC = 10 oC or 10 K
Now,
(i) Heat capacity = Mass × specific heat capacity
= 0.2 kg × 410 Jkg-1K-1
= 82 J K-1
(ii) Energy required to increase the temperature of vessel
ΔQ = mcΔT
= 0.2 X 410 X 10
= 820 J
Solution E.3
(i)We know that heat energy needed to raise the temperature by 15o is = heat capacity x change in temperature.
Heat energy required= 966 J K-1 x 15 K = 14490 J.
(ii)We know that specific heat capacity is = heat capacity/ mass of substance
So specific heat capacity is = 966 / 2=483 J kg-1 K-1.
Solution E.4
Mass of copper m = 200 g = 0.2 kg
Change of temperature Δt = (70-20) = 50 oC or 50 K
Specific heat of capacity of copper =390 J kg-1 K-1
Amount of heat required to raise the temperature of 0.1 kg of copper is
Q = mcΔT
Q = 0.2 x 50 x 390
= 3900 J
Solution E.5
Q = 1300 J
m = 0.5 kg
ΔT = 40°C - 20°C = 20°C or 20 K
Now,
Q= mcΔT
i.e., 1300 = 0.5 × 20 × c
![]()
∴ c = 130 J/kg K
Solution E.6
Specific heat capacity of material c =960 J kg-1 K-1
Change in temperature ![]() T=(38-18)oC = 20oC (or 20 K)
T=(38-18)oC = 20oC (or 20 K)
Power of heater P = 500 W
![]()
![]()
Time taken by a heater to raise the temperature of material
![]()
![]()
t= 1920 seconds
t=32 min
Solution E.7
Power of heater P= 600 W
Mass of liquid m=4.0 kg
Change in temperature of liquid = (15-10)oC = 5oC(or 5 K)
Time taken to raise its temperature =100s
Heat energy required to heat the liquid
![]()
and
![]() =600X100=60000J
=600X100=60000J
![]() =
=![]()
Heat capacity= c x m
Heat capacity= 4 x 3000JKg-1 K-1 = 1.2 x 104 J/K
Solution E.8
Change in temperature= 30 - 5 = 25 K.
![]()
![]()
![]() =
=![]()
t=29 min 10 sec.
Solution E.9
Heat liberated by metal=![]()
Heat absorbed by water=![]()
Heat energy lost= heat energy gained
![]() =
=![]()
S=0.52 J g-1 K-1.
Solution E.10
Mass of water (m1)=45 g
Temperature of water (T1) =50oC
Mass of copper (m2) =50 g
temperature of copper(T2) =18oC
Final temperature (T) =?
The specific heat capacity of the copper c2 = 0.39 J/g/K
The specific heat capacity of water c1 = 4.2 J/g/K
![]()
![]()
![]() oC
oC
T= 47oC.
Solution E.11
Given that,
Mass of hot water (m1) = 200g
Temperature of hot water (T1) = 80oC
Mass of cold water (m2) = 400g
Temperature of cold water (T2) =10oC
Final temperature (T) =?
![]()
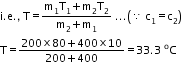
Solution E.12
Mass of hot water (m1) = 300 g
Temperature (T1) = 50oC
Mass of cold water (m2) = 600 g
Change in temperature of cold water (T-T2) =15oC
Final temperature =ToC
The specific heat capacity of water is c.
![]()
![]()
T = 20oC.
Final temperature = 20o c
Change in temperature = 15oC
Initial temperature of cold water = 20oC -15oC = 5oC.
Solution E.13
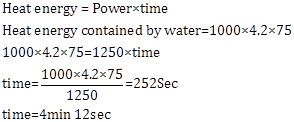
Calorimetry Exercise Ex. 11B
Solution A.1
(d) absorbed, rejected
Heat energy is absorbed during melting and rejected during freezing at a constant temperature.
Solution A.2
(c) ice
Substances like lead, wax, etc., expand on melting.
Whereas substances like ice, bismuth, etc. contract on melting
Solution A.3
(c) decrease
The melting point decreases for the substance which contracts on melting (Example: Ice).
Solution A.4
(c) less than 100°C
The boiling point of liquid increases with an increase in pressure and decreases with a decrease in pressure.
In the given case, atmospheric pressure decreases at high altitudes. Thus, the boiling point of water decreases, too.
Solution A.5
(c) higher than 100°C
Adding impurities such as salt or sugar can increase the boiling point of water. When salt is added, the boiling point of water will be greater than 100°C.
Solution A.6
(c) J kg-1
![]()
∴ L = Q/m
i.e., S.I. unit of Specific latent heat (L) = J/kg or J kg-1
Solution A.7
(c) J kg-1
Solution A.8
(a) 80 cal g-1
Solution B.1
In a pressure cooker, the water boils at about 120oC to 125oC.
Solution B.2
(a) When ice melts, its volume decreases.
(b) Decrease in pressure over ice increases its meltingpoint.
(c) Increase in pressure increases the boiling point of water.
(d)A pressure cooker is based on the principle that boiling point of water increases with the increase in pressure.
(e) The boiling point of water is defined as the constant temperature at which water changes to steam.
(f) water can be made to boil at 115°C by increasing pressure over its surface.
Solution B.3
Specific latent heat of ice: 336000 J kg-1.
Solution B.4
Latent heat is absorbed by ice.
Solution C.1
(i)Average kinetic energy of molecules changes.
(ii)Average potential energy of molecules changes.
Solution C.2
(a) Average kinetic energy does not change.
(b) Average potential energy increases.
Explanation: When a substance is heated at constant temperature (i.e. during its phase change state), the heat supplied makes the vibrating molecules gain potential energy to overcome the intermolecular force of attraction and move about freely. This means that the substance changes its form.
However, this heat does not increase the kinetic energy of the molecules, and hence, no rise in temperature takes place during the change in phase of a substance.
This heat supplied to the substance is known as latent heat and is utilized in changing the state of matter without any rise in temperature.
Solution C.3
The melting point of ice decreases by the presence of impurity in it.
Use: In making the freezing mixture by adding salt to ice. This freezing mixture is used in preparation of ice creams.
Solution C.4
The melting point of ice decreases by the increase in pressure. The melting point of ice decrease by 0.0072oC for every one atmosphere rise in pressure.
Solution C.5
The boiling point of water increases on adding salt.
Solution C.6
The boiling point of a liquid increases on increasing the pressure.
Solution C.7
- The boiling point of a liquid increases with the increase in pressure and decreases with the decrease in pressure.
- The boiling point of pure water at one atmospheric pressure (= 760 mm of Hg) is 100 °C.
- In a pressure cooker, the water boils at about 120 °C to 125 °C due to increase in pressure, as the steam is not allowed to escape out of it.
Solution C.8
This is because at high altitudes atmospheric pressure is low; therefore boiling point of water decreases and so it does not provide the required heat energy for cooking.
Solution C.9
Latent heat: The heat energy exchanged in change of phase is not externally manifested by any rise or fall in temperature, it is considered to be hidden in the substance and is called the latent heat.
Solution C.10
The quantity of heat required to convert unit mass of ice into liquid water at ![]() (melting point) is called the specific latent heat of fusion of ice.
(melting point) is called the specific latent heat of fusion of ice.
Its S.I. unit is Jkg-1.
Solution C.11
It means 1 g of ice at 0oC absorbs 360 J of heat energy to convert into water at 0oC.
Solution C.12
1 g of water at 0oC has more heat than 1 g of ice at 0oC. This is because ice at 0oC absorbs 360 J of heat energy to convert into water at 0oC.
Solution C.13
(a) 1 g ice at 0oC requires more heat because ice would require additional heat energy equal to latent heat of melting.
(b) 1 g ice at 0oC first absorbs 336 J heat to convert into 1 g water at 0oC.
Solution C.14
This is because 1 g of ice at 0oC takes 336 J of heat energy from the mouth to melt at 0oC. Thus mouth loses an additional 336 J of heat energy for 1 g of ice at 0oC than for 1g of water at 0oC. Therefore cooling produced by 1 g of ice at 0oC is more than for 1g of water at 0oC.
Solution C.15
This is because 1 g of ice at 0oC takes 336 J of heat energy from the bottle to melt into water at 0oC. Thus bottle loses an additional 336 J of heat energy for 1 g of ice at 0oC than for 1 g iced water at 0oC. Therefore bottled soft drinks get cooled, more quickly by the ice cubes than by iced water.
Solution C.16
The reason is that after the hail storm, the ice absorbs the heat energy required for melting from the surrounding, so the temperature of the surrounding falls further down and we feel colder.
Solution C.17
The reason is that the heat energy required for melting the frozen lake is absorbed from the surrounding atmosphere. As a result, the temperature of the surrounding falls and it became very cold.
Solution C.18
The specific latent heat of fusion of ice is sufficiently high, about 336 J g-1. Before freezing the water in the lakes and ponds will have to release a large quantity of heat to the surrounding. If there is any layer of ice formed on water than water being a poor conductor of heat will also prevent the loss of heat from water of lake. Hence, in cold countries water in lakes and ponds do not freeze.
Solution D.1
(a) The process of change from one state to another at a constant temperature is called the change of phase of substance.
(b)There is no change in temperature during the change of phase.
(c)Yes, the substance absorbs or liberates heat during the change of phase.
(d) Latent heat
Solution D.2
(a) Melting.
(b) Latent heat of melting.
(c) As their id no change in temperature the average kinetic energy of the molecules does not change.
Solution D.3
(a) AB part shows rise in temperature of solid from 0 to T1oC, BC part shows melting at temperature T1oC, CD part shows rise in temperature of liquid from T1oC to T3oC , DE part shows the boiling at temperature T3oC.
(b) T1oC.
(c) T3oC.
Solution D.4
The melting point of naphthalene , a crystalline solid is 80 degree C and the room temperature is 25 °C
The temperature - time graph is as follows: -
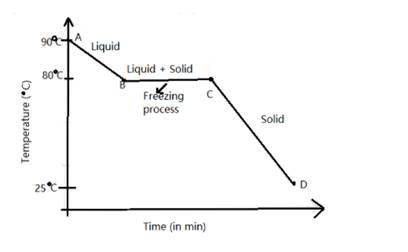
Solution D.5
Solution D.6
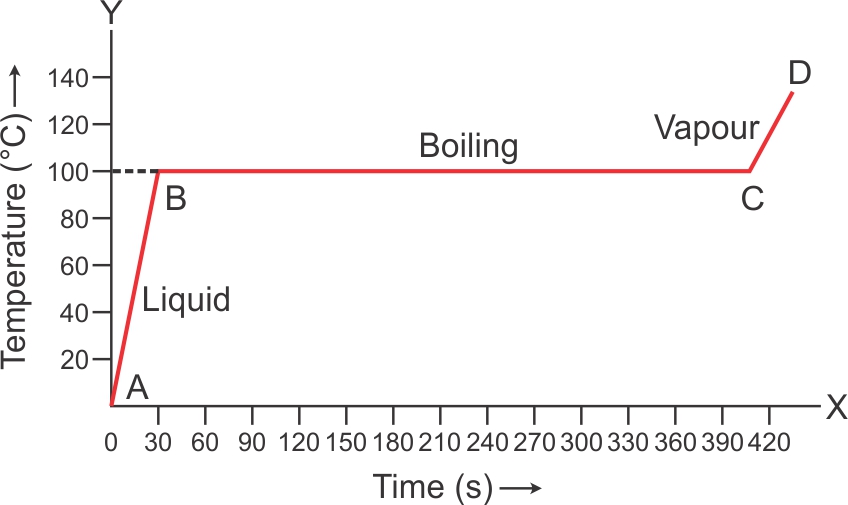
Boiling: The change from liquid to gaseous phase on heating at a constant temperature is called boiling.
Boiling Point: The particular temperature at which vaporization occurs is called the boiling point of liquid.
Volume of water wills increases when it boils at 100oC.
Solution D.7
(i) The reason is that the specific latent heat of fusion of ice is sufficiently high, so when the water of lake freezes, a large quantity of heat has to be released and hence the surrounding temperature becomes pleasantly warm.
(ii) Heat supplied to a substance during its change of state, does not cause any rise in its temperature because this is latent heat of phase change which is required to change the phase only.
Solution E.1
Given that,
Mass of ice, m = 20 g = 0.02 kg
ΔT = 50°C - 0°C = 50°C or 50 K
Specific heat capacity of water, c = 4200 J kg-¹ K-¹.
Total Heat energy required, Q = 10920 J
Now,
The heat energy required to melt ice is given by:
Q1 = m × Lf
The heat energy required to raise the temperature of melted ice from 0°C to 50°C is given by: Q2 = mcΔT = 0.02 × 4200 × 50 = 4200 J.
The total heat energy required is given by:
Q1 + Q2 = 10920 J
0.02 kg × Lf = 6720 J
Lf = 336000 J kg⁻¹ = 336 J/g
Solution E.2
Mass of water m = 5.0 g
specific heat capacity of water c = 4.2 J g-1 K-1
specific latent heat of fusion of iceL =336 J g-1
Amount of heat energy released when 5.0 g of water at 20oC changes into water at 0oC = 5 x 4.2 x 20 = 420 J.
Amount of heat energy released when 5.0g of water at 0oC changes into ice at 0oC=5x336J=1680J.
Total amount of heat released =1680 J + 420 J = 2100 J.
Solution E.3
Mass of metal =150 g
Specific latent heat of metal
![]()
Specific heat capacity of metal is 200 J kg-1 K-1.
Change in temperature= 800-(-50) = 850oC (or 850 K).
![]()
Solution E.4
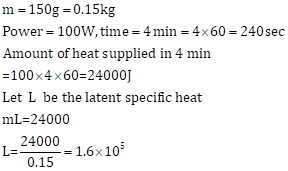
Solution E.5
Amount of heat released when 100g of water cools from 20o to 0oC =100X20X4.2=8400J.
Amount of heat released when 100g of water converts into ice at 0oC =100X336=33600J.
Amount of heat released when 100g of ice cools from 0oC to -10oC =100X10X2.1=2100J.
Total amount of heat=8400+33600+2100=44100J.
Time taken= 73.5min=4410s.
Average rate of heat extraction (power)
![]() .
.
Solution E.6
Mass of ice m1 =17 g
Mass of water m2 =40 g.
Change in temperature =34-0=34K
Specific heat capacity of water is 4.2Jg-1K-1.
Assuming there is no loss of heat, heat energy gained by ice (latent heat of ice), Q= heat energy released by water
Q = 40 x 34 x 4.2 = 5712 J.
Specific latent heat of ice=![]() .
.
Solution E.7
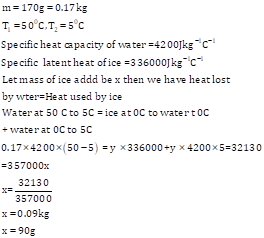
Solution E.8
Let whole of the ice melts and let the final temperature of the mixture be ToC.
Amount of heat energy gained by 10g of ice at -10oC to raise its temperature to 0oC= 10x10x2.1=210J
Amount of heat energy gained by 10g of ice at 0oC to convert into water at 0oC=10x336=3360 J
Amount of heat energy gained by 10g of water (obtained from ice) at 0oC to raise its temperature to ToC = 10x4.2x(T-0)=42T
Amount of heat energy released by 10g of water at 10oC to lower its temperature to ToC = 10x4.2x(10-T)=420-42T
Heat energy gained = Heat energy lost
210 + 3360 + 42T = 420-42T
T = -37.5oC
This cannot be true because water cannot exist at this temperature.
So whole of the ice does not melt. Let m gm of ice melts. The final temperature of the mixture becomes 0oC.
So, amount of heat energy gained by 10g of ice at -10oC to raise its temperature to 0oC= 10x10x2.1=210J
Amount of heat energy gained by m gm of ice at 0oC to convert into water at 0oC=mx336=336m J
Amount of heat energy released by 10g of water at 10oC to lower its temperature to 0oC = 10x4.2x(10-0)=420
Heat energy gained = Heat energy lost
210 + 336m = 420
m = 0.625 gm
Solution E.9
Let final temperature of water when all the ice has melted =ToC.
Amount of heat lost when 200g of water at 50oC cools to ToC=
200X4.2X(50-T) = 42000-840T
Amount of heat gained when 40g of ice at 0oC converts into water at 0oC.= 40X336J = 13440 J
Amount of heat gained when temperature of 40g of water at 0oC rises to ToC= 40X4.2X(T-0) = 168T
We know that
Amount of heat gained=amount of heat energy lost.
13440+168T= 42000-840T
168T+840T= 42000-13440
1008T= 28560
T=28560/1008=28.33oC.
Solution E.10
Heat loss by (water+Calorimeter) = Heat gain by ice
Heat loss by (water+calorimeter) = mw Cpw ΔT + mC Cpc ΔT = mi ( L + Cpw δT ) ......................(1)
where, mw = mass of water = 50 g
Cpw = Specific heat of water = 4.2 J/( g °C )
mC = mass of calorimeter = 50 g
Cpc = Specific heat capacity of calorimeter = 0.4 J/( g °C )
ΔT = fall in temperature of water and calorimeter = 32-5 = 27°C
mi = mass of ice in gram
L = latent heat capacity of ice = 330 J/g
δT = rise in temperature = 5 °C
by substituting all the values in eqn.(1)we get the mass of ice as
![]()
Solution E.11
Mass of copper vessel m1 = 50 g.
Mass of water contained in copper vessel m2 = 250 g.
Mass of ice required to bring down the temperature of vessel = m
Final temperature = 5o C.
Amount of heat gained when 'm' g of ice at 0o C converts into water at 0o C = m × 336 J
Amount of heat gained when temperature of 'm' g of water at 0o C rises to 5o C = m × 4.2 × 5
Total amount of heat gained = m × 336 + m × 4.2 × 5
Amount of heat lost when 250 g of water at 30o C cools to 5o C =
250 × 4.2 x 25 = 26250 J
Amount of heat lost when 50 g of vessel at 30o C cools to 5o C =
50 x 0.4 × 25 = 500 J
Total amount of heat lost = 26250 + 500 = 26750 J
We know that amount of heat gained = amount of heat lost
m × 336 + m × 4.2 × 5 = 26750
357 m = 26750
m = 26750/357 = 74.93 g
Hence, mass of ice required is 74.93 g.
Solution E.12
Since the whole block does not melt and only 2 kg of it melts, so the final temperature would be 0 oC.
Amount of heat energy gained by 2 kg of ice at 0oC to convert into water at 0oC=2X336000=672000 J
Let amount of water poured=m kg.
Initial temperature of water =100oC.
Final temperature of water =0oC.
Amount of heat energy lost by m kg of water at 100oC to reach temperature 0oC =mX4200X100 = 420000m J
We know that heat energy gained =heat energy lost.
672000J= mX420000J
m=672000/420000=1.6kg
Solution E.13
Amount of heat energy gained by 100 g of ice at -10o C to raise its temperature to 0o C =
100 × 2.1 × 10 = 2100 J
Amount of heat energy gained by 100 g of ice at 0o C to convert into water at 0o C =
100 × 336 = 33600 J
Amount of heat energy gained when temperature of 100 g of water at 0o C rises to 100o C =
100 × 4.2 × 100 = 42000 J
Total amount of heat energy gained is = 2100 + 33600 + 42000 = 77700 J = 7.77 × 104 J
Solution E.14
Amount of heat energy gained by 1kg of ice at -10oC to raise its temperature to 0oC= 1 x 2100 x 10 = 21000 J
Amount of heat energy gained by 1kg of ice at 0oC to convert into water at 0oC=L
Amount of heat energy gained when temperature of 1kg of water at 0oC rises to 100oC= 1 x 4200 x 100 = 420000 J
Total amount of heat energy gained = 21000+420000+L=441000 +L.
Given that total amount of heat gained is =777000J.
So,
441000+L=777000.
L=777000-441000.
L=336000JKg-1
Solution E.15
Mass of ice, mice = 200 g
Time for ice to melt, t1 = 1 min = 60 s
Mass of water, mw = 200 g
Temperature change of water, ΔT = 20 °C
Rate of heat exchange is constant. So, power required for converting ice to water is same as the power required to increase the temperature of water.
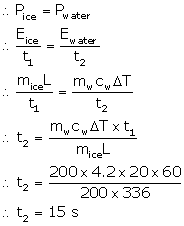
Hence, the time required is 15 seconds.

