Class 10 SELINA Solutions Maths Chapter 21 - Trigonometrical Identities (Including Trigonometrical Ratios of Complementary Angles and Use of Four Figure Trigonometrical Tables)
Trigonometrical Identities (Including Trigonometrical Ratios of Complementary Angles and Use of Four Figure Trigonometrical Tables) Exercise TEST YOURSELF
Solution 1(i)
Correct option: (i) 45o
sin 2x = 2 sin 45o cos 45o
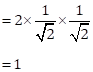
Then, sin 2x = sin 90o
2x = 90o⇒ x = 45o
Solution 1(h)
Correct option: (iii) 1
Solution 1(g)
Correct option: (i) tan 30o
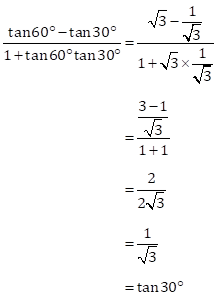
Solution 1(f)
Correct option: (iii) x2 + y2
M = x cos A + y sin A and N = x sin A – y cos A
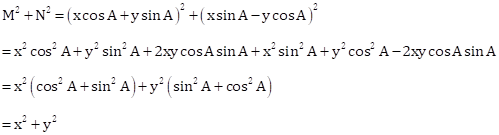
Solution 1(e)
Correct option: (ii) B and C
The value of sin increases from 0 to 1 and the value of tan increases from 0 to infinity.
Therefore, for two acute angles ⍺ and β, if ⍺ > β, then
tan ⍺ > tan β and sin ⍺ > sin β.
Solution 1(d)
Correct option: (ii) sec A
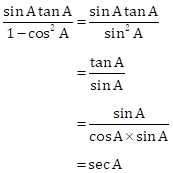
Solution 1(c)
Correct option: (iii) 0
(1 + tan2 A) × cos2 A – 1
= sec2A × cos2 A – 1
= 1 – 1
= 0
Solution 1(b)
Correct option: (iv) 
Solution 1(a)
Correct option: (i) cot γ < cot β
The value of cot decreases from 0 to infinity.
Therefore, for three acute angles ⍺, β and γ, where ⍺ < β < γ,
cot γ < cot β.
Solution 2
(i) 
(ii) 
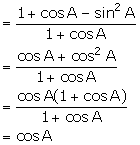
(iii) 
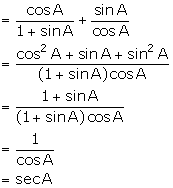
(iv) 
(5) 
(vi)
(vii) 
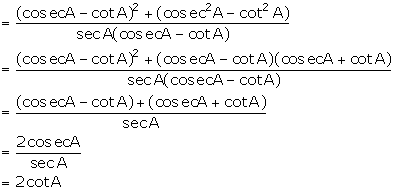
(viii) 
(ix) 
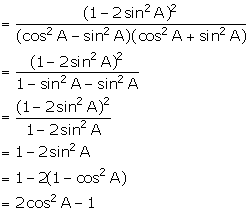
(x) 
(xi) 
Solution 3
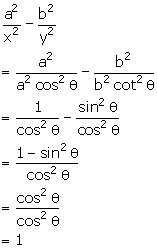
Solution 4
Solution 5
(i) 2 sinA - 1 = 0
(ii)
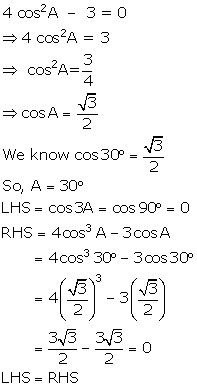
Solution 6
(i) 
(ii) 
(iii) 
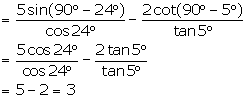
(iv) 
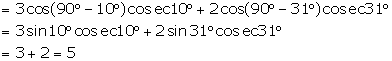
Solution 7
(i) 
(ii) 
(iii) 
(iv) 
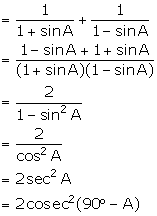
Solution 8
Since, A and B are complementary angles, A + B = 90°
(i)
(ii)
(iii)
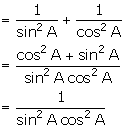
= cosec2A [sec(90 - B)]2
= cosec2A cosec2B
(iv) 
Solution 9
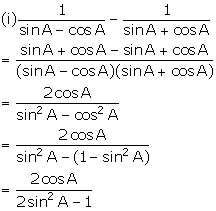
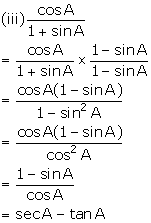
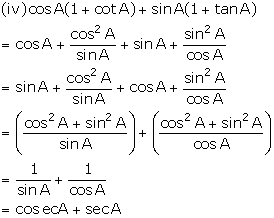
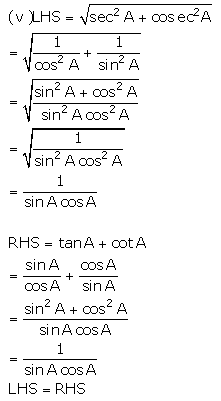
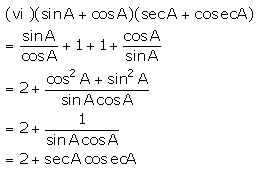
Solution 10
4 cos2A - 3 = 0
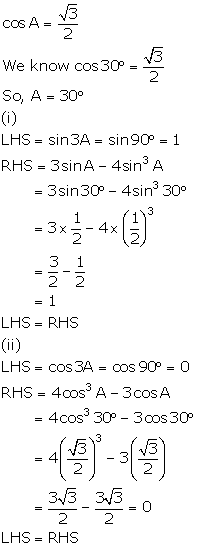
Solution 11
(i) 
(ii) sin 3A - 1 = 0
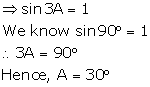
(iii) 
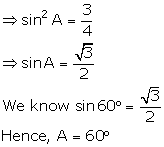
(iv) 
(v) 
Solution 12
(i) 
(ii) 
Solution 13
_ASH_files/20141209110714_image002.gif)
Solution 14
Solution 15
sin2 28° + sin2 62° + tan2 38° - cot2 52° + 
sec2 30°
= sin2 28° + [sin (90 - 28)°]2 + tan2 38° - [cot(90 - 38)°]2 + sec2 30°
= sin2 28° + cos2 28° + tan2 38°- tan2 38° + sec2 30°
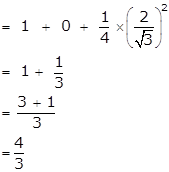
Trigonometrical Identities (Including Trigonometrical Ratios of Complementary Angles and Use of Four Figure Trigonometrical Tables) Exercise Ex. 21(A)
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
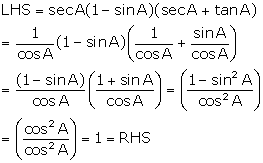
Solution 7
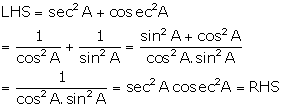
Solution 8
Solution 9
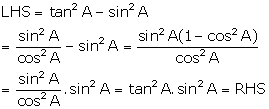
Solution 10
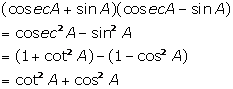
Solution 11
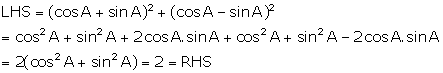
Solution 12
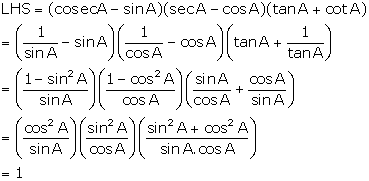
Solution 13
Solution 14
Solution 15
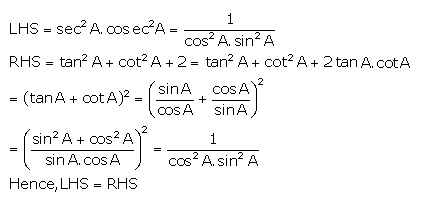
Solution 16
Solution 17
Solution 18
Solution 19
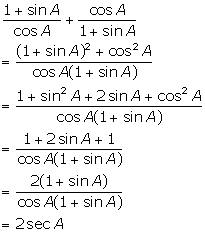
Solution 20
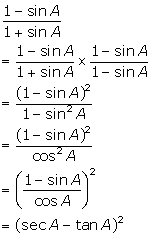
Solution 21
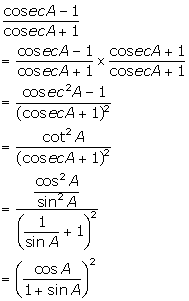
Solution 22
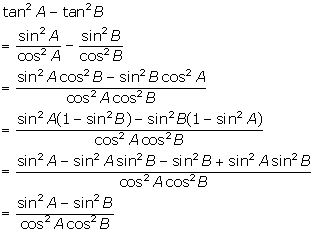
Solution 23
To prove: 
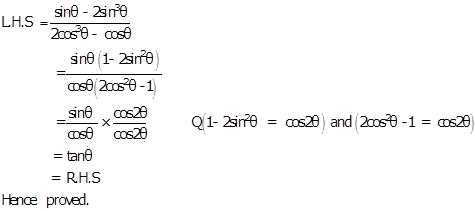
Solution 24
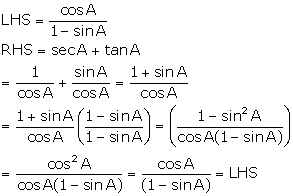
Solution 25
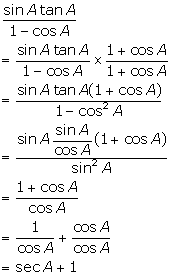
Solution 26
Solution 27
Solution 28
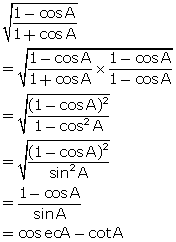
Solution 29
Solution 30
Solution 31
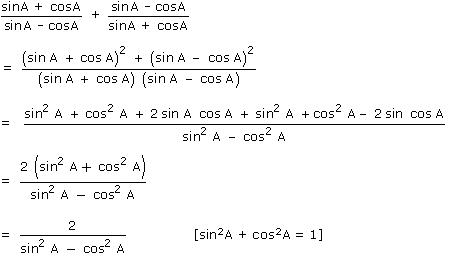
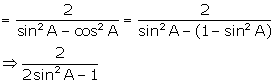
Solution 32
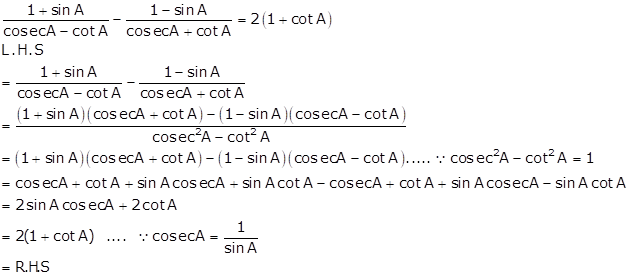
Solution 33
Solution 1(e)
Correct option: (ii) 
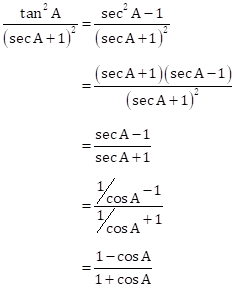
Solution 1(d)
Correct option: (ii) sec2 A(1 + sin A)
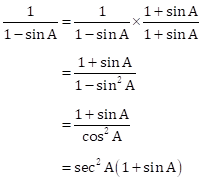
Solution 1(c)
Correct option: (iv) cosec4 Ɵ – cosec2 Ɵ
cot4 Ɵ + cot2 Ɵ = cot2 Ɵ(cot2 Ɵ + 1)
= cot2 Ɵ.cosec2 Ɵ
= (cosec2 Ɵ – 1)cosec2 Ɵ
= cosec4 Ɵ – cosec2 Ɵ
Solution 1(b)
Correct option: (ii) 2sec2 Ɵ
(1 + tan Ɵ)2 + (1 – tan Ɵ)2
= (1 + tan2 Ɵ + 2tan Ɵ) + (1 + tan2 Ɵ – 2tan Ɵ)
= (sec2 Ɵ + 2tan Ɵ) + (sec2 Ɵ – 2tan Ɵ)
= 2sec2 Ɵ
Solution 1(a)
Correct option: (iii) 2sin2 Ɵ – 1
sin4 Ɵ – cos4 Ɵ = (sin2 Ɵ)2 – (cos2 Ɵ)2
= (sin2 Ɵ – cos2 Ɵ)(sin2 Ɵ + cos2 Ɵ)
= (sin2 Ɵ – cos2 Ɵ)(1)
= sin2 Ɵ – (1 – sin2 Ɵ)
= sin2 Ɵ – 1 + sin2 Ɵ
= 2sin2 Ɵ – 1
Trigonometrical Identities (Including Trigonometrical Ratios of Complementary Angles and Use of Four Figure Trigonometrical Tables) Exercise Ex. 21(B)
Solution 2
(ii)
(iii)
(iv)
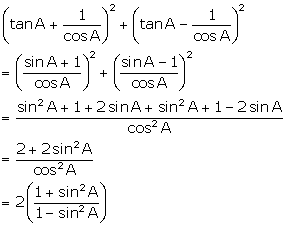
(v)
(vi)
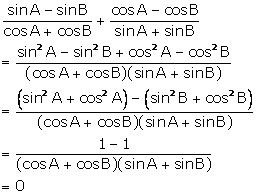
(vii)
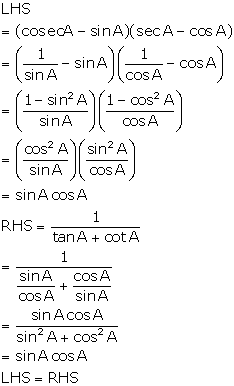
(viii)
(ix)
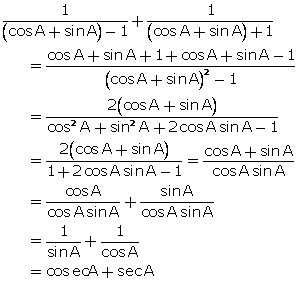
Solution 3
Solution 4
Solution 5
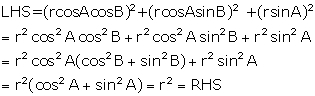
Solution 6
LHS = (m2 + n2) cos2B
Hence, (m2 + n2) cos2B = n2.
Solution 1(a)
Correct option: (iv) sec2 A.cosec2 A
(1 + cot2 A) + (1 + tan2 A)
= cosec2 A + sec2 A
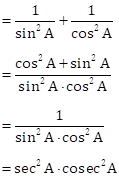
Solution 1(b)
Correct option: (iii) b2 – a2 = 1
b2 – a2 = sec2Ɵ – tan2 Ɵ = 1
Solution 1(c)
Correct option: (ii) sin Ɵ . cos Ɵ
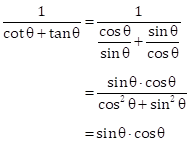
Solution 1(d)
Correct option: (iv) –4
(sec Ɵ – cos Ɵ)2 – (sec Ɵ + cos Ɵ)2
= (sec2 Ɵ + cos2 Ɵ – 2sec Ɵ cos Ɵ) – (sec2 Ɵ + cos2 Ɵ + 2sec Ɵ cos Ɵ)
= sec2 Ɵ + cos2 Ɵ – 2sec Ɵ cos Ɵ – sec2 Ɵ – cos2 Ɵ – 2sec Ɵ cos Ɵ
= –4sec Ɵ cos Ɵ
= –4
Solution 1(e)
Correct option: (iv) cosec2 A . cosec2 B
(cot A – cot B)2 + (1 + cot A cot B)2
= cot2 A + cot2 B – 2cot A cot B + 1 + cot2 A cot2 B + 2cot A cot B
= (cot2 A + 1) + cot2 B(1 + cot2 A)
= (cot2 A + 1)(cot2 B + 1)
= cosec2 A . cosec2 B
Solution 2(i)
L.H.S. = (sec A – tan A)2(1 + sin A)
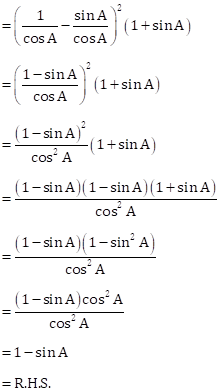
Trigonometrical Identities (Including Trigonometrical Ratios of Complementary Angles and Use of Four Figure Trigonometrical Tables) Exercise Ex. 21(C)
Solution 2
(i)
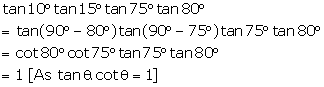
(ii)
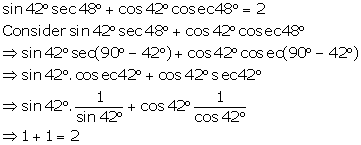
Solution 3
Solution 4
(i) 
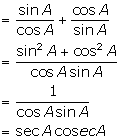
(ii) 
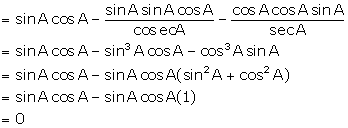
Solution 5
(i) We know that for a triangle 
ABC
A + B + C = 180°
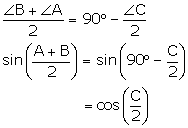
(ii) We know that for a triangle ABC
A + B + C = 180°
B + C = 180° - A
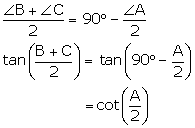
Solution 6
(i) 
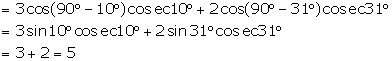
(ii) 
(iii) 
(iv) 
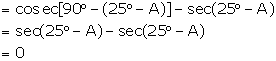
(v) 
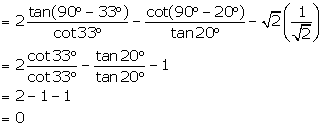
(vi) 
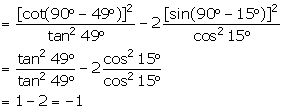
(vii) 
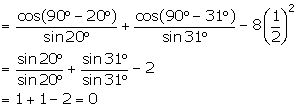
Solution 7
Since, ABC is a right angled triangle, right angled at B.
So, A + C = 90
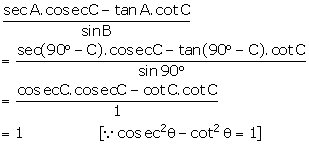
Solution 8
(i) 
Hence, x = 
(ii) 
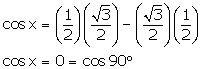
Hence, x =
(iii) 
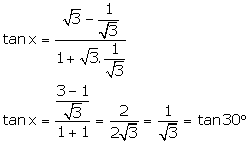
Hence, x = 
(iv) 
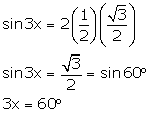
Hence, x = 
(v) 
Hence, 
Solution 9
(i) 
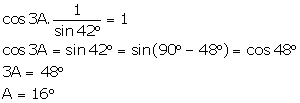
(ii) 
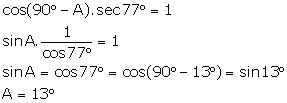
Solution 10
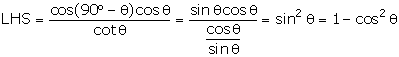
Solution 11
Solution 12
Solution 13
Solution 1(a)
Correct option: (ii) 1
sin2 A + sin2(90o – A)
= sin2 A + cos2 A
= 1
Solution 1(b)
Correct option: (i) 
In a triangle ABC,
A + B + C = 180o
A + C = 180o – B
Now, sec 
Solution 1(c)
Correct option: (iii) 3
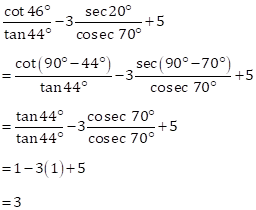
Solution 1(d)
Correct option: (iv) 1
sin 67o . cos 23o + cos 67o . sin 23o
= sin (90o – 23o) . cos 23o + cos (90o – 23o) . sin 23o
= cos 23o . cos 23o + sin 23o . sin 23o
= cos2 23o + sin2 23o
= 1
Solution 1(e)
Correct option: (ii) sin2 Ɵ
Trigonometrical Identities (Including Trigonometrical Ratios of Complementary Angles and Use of Four Figure Trigonometrical Tables) Exercise Ex. 21(D)
Solution 2
(i) sin 21o = 0.3584
(ii) sin 34o 42'= 0.5693
(iii) sin 47o 32'= sin (47o 30' + 2') =0.7373 + 0.0004 = 0.7377
(iv) sin 62o 57' = sin (62o 54' + 3') = 0.8902 + 0.0004 = 0.8906
Solution 3
(i) cos 2° 4’ = 0.9994 - 0.0001 = 0.9993
(ii) cos 8° 12’ = cos 0.9898
(iii) cos 26° 32’ = cos (26° 30’ + 2’) = 0.8949 - 0.0003 = 0.8946
(iv) cos 65° 41’ = cos (65° 36’ + 5’) = 0.4131 -0.0013 = 0.4118
Solution 3
(i) tan 37o = 0.7536
(ii) tan 42o 18' = 0.9099
Solution 5
(i) From the tables, it is clear that sin 29o = 0.4848
Hence, 
= 29o
(ii) From the tables, it is clear that sin 22o 30' = 0.3827
Hence, = 22o 30'
Solution 6
(i) From the tables, it is clear that cos 10° = 0.9848
Hence, 
= 10°
(ii) From the tables, it is clear that cos 16° 48’ = 0.9573
cos - cos 16° 48’ = 0.9574 - 0.9573 = 0.0001
From the tables, diff of 1’ = 0.0001
Hence, = 16° 48’ - 1’ = 16° 47’
Solution 7
(i) From the tables, it is clear that tan 13° 36’ = 0.2419
Hence, 
= 13° 36’
(ii) From the tables, it is clear that tan 25° 18’ = 0.4727
tan - tan 25° 18’ = 0.4741 - 0.4727 = 0.0014
From the tables, diff of 4’ = 0.0014
Hence, = 25° 18’ + 4’ = 25° 22’
Solution 1(a)
Correct option: (iv) 2cos Ɵ = 1
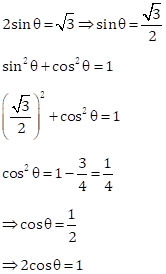
Solution 1(b)
Correct option: (i) 1 + x2
1 + sin2 27o20’
= 1 + sin2(90o – 62o40’)
= 1 + sin2(89o60’ – 62o40’)
= 1 + cos2 62o40’
= 1 + x2
Solution 1(c)
Correct option: (iii) 
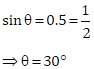
Then,
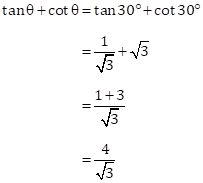
Solution 1(d)
Correct option: (iii) 0.4446
cos 63o36’ = 0.4446
cos(90o – 26o24’) = 0.4446
cos(89o60’ – 26o24’) = 0.4446
sin 26o24’ = 0.4446
