Class 10 SELINA Solutions Maths Chapter 12: Reflection (In x-axis, y-axis, x=a, y=a and the origin ; Invariant Points)
Reflection (In x-axis, y-axis, x=a, y=a and the origin ; Invariant Points) Exercise TEST YOURSELF
Solution 1(f)
Correct option: (iv) Δ ABC ≠ Δ A”B”C”
As ABC is reflected in y-axis, so only x-coordinate of each vertex will change by a negative sign.
As A’B’C’ is reflected in the line y = 0 i.e. x-axis, so only y-coordinate of each vertex will change by a negative sign.
The lengths of the sides and the angles remains the same.
Thus, Δ A’B’C’ ∼Δ A”B”C”, Δ A’B’C’≅Δ A”B”C” and Δ ABC ≅Δ A”B”C”.
Also, Δ ABC = Δ A”B”C”.
Solution 1(e)
Correct option: (iv) no-one
Let P ≡ (a, b)
When P is reflected in x = 0 i.e. y-axis, we get P’ ≡ (–a, b).
When P’(–a, b) is reflected in y = 0 i.e. x-axis, we get P” ≡ (–a, –b).
Thus, no two points are invariant.
Solution 1(d)
Correct option: (i) (10, 0)
As (5, 7) is reflected in x-axis, so the coordinates of P’ are (5, –7).
O’ is the image of origin O in the line PP’.
So, the coordinates of O’ are (10, 0).
Solution 1(c)
Correct option: (ii) y’ = x’
The point P(x, y) is reflected in the line y = x to point P’(x’, y’), then y’ = x’.
Solution 1(b)
Correct option: (i) Point A
Let A ≡ (a, b)
When A is reflected in y-axis, we get B ≡ (–a, b).
When B is reflected in origin, we get C ≡ (a, –b).
When C is reflected in y = 0 i.e. x-axis, we get P ≡ (a, b).
Therefore, point A coincides with point P.
Solution 1(a)
Correct option: (iv) y-axis
When (5, 6) is reflected in a line to get the point (–5, 6), only x-coordinate changes.
Therefore, the line of reflection is y-axis.
Solution 2
Reflection in y-axis is given by My (x, y) = (-x, y)
A' = Reflection of A(4, -1) in y-axis = (-4, -1)
Reflection in x-axis is given by Mx (x, y) = (x, -y)
B' = Reflection of B in x-axis = (-2, 5)
Thus, B = (-2, -5)
Solution 3
(a) We know that reflection in the line x = 0 is the reflection in the y-axis.
It is given that:
Point (-5, 0) on reflection in a line is mapped as (5, 0).
Point (-2, -6) on reflection in the same line is mapped as (2, -6).
Hence, the line of reflection is x = 0, that is y-axis.
(b) It is known that My (x, y) = (-x, y)
Co-ordinates of the image of (5, -8) in y-axis are (-5, -8).
Solution 4
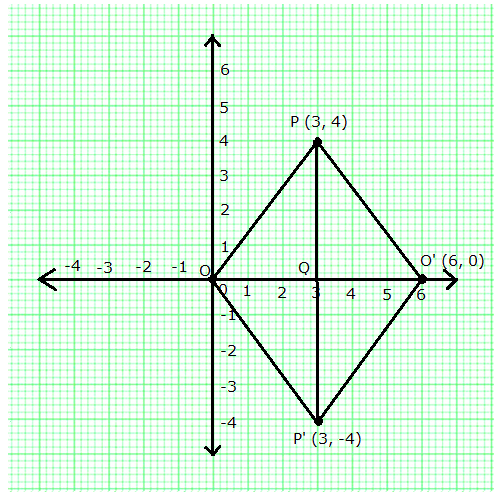
(i) Co-ordinates of P' and O' are (3, -4) and (6, 0) respectively.
(ii) PP' = 8 units and OO' = 6 units.
(iii) From the graph it is clear that all sides of the quadrilateral POP'O' are equal.
In right ![]() PQO',
PQO',
PO' = ![]()
So, perimeter of quadrilateral POP'O' = 4 PO' = 4 ![]() 5 units = 20 units
5 units = 20 units
(iv) Quadrilateral POP'O' is a rhombus.
Solution 5
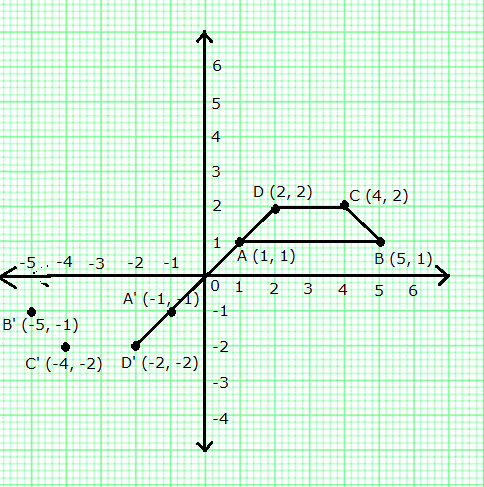
Quadrilateral ABCD is an isosceles trapezium.
Co-ordinates of A', B', C' and D' are A'(-1, -1), B'(-5, -1), C'(-4, -2) and D'(-2, -2) respectively.
It is clear from the graph that D, A, A' and D' are collinear.
Solution 6
(a) Any point that remains unaltered under a given transformation is called an invariant.
It is given that P (0, 5) is invariant when reflected in an axis. Clearly, when P is reflected in the y-axis then it will remain invariant. Thus, the required axis is the y-axis.
(b) The co-ordinates of the image of Q (-2, 4) when reflected in y-axis is (2, 4).
(c) (0, k) on reflection in the origin is invariant. We know the reflection of origin in origin is invariant. Thus, k = 0.
(d) Co-ordinates of image of Q (-2, 4) when reflected in origin = (2, -4)
Co-ordinates of image of (2, -4) when reflected in x-axis = (2, 4)
Thus, the co-ordinates of the point are (2, 4).
Solution 7
(a) P (2, -4) is reflected in (x = 0) y-axis to get Q.
P(2, -4) ![]() Q (-2, -4)
Q (-2, -4)
(b) Q (-2, -4) is reflected in (y = 0) x-axis to get R.
Q (-2, -4) ![]() R (-2, 4)
R (-2, 4)
(c) The figure PQR is right angled triangle.
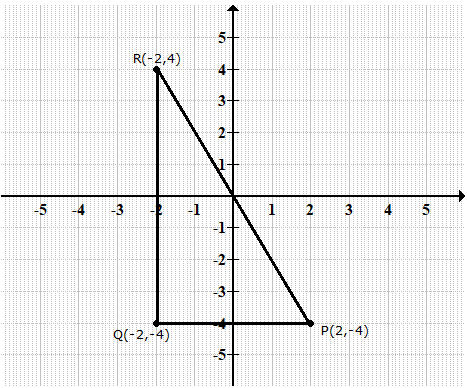
(d) Area of ![]()
Solution 8
(a)

Solution 9
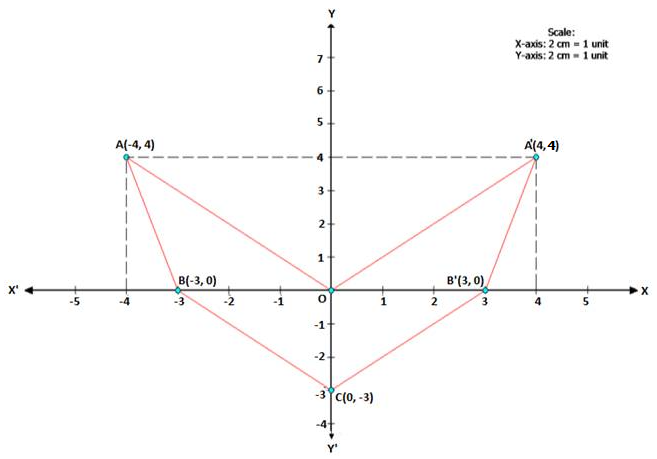
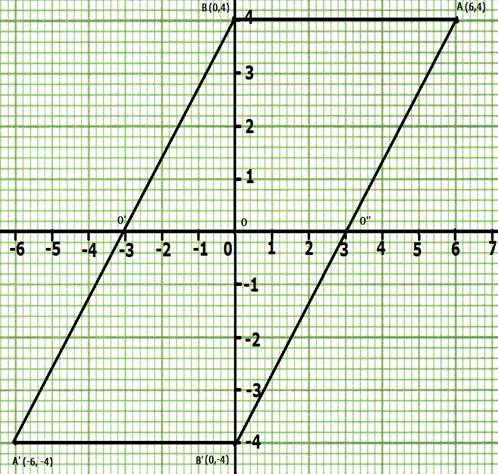
i. A' = (4, 4) AND B' = (3, 0)
ii. The figure is an arrow head.
Solution 10
(i)Plotting A(0,4), B(2,3), C(1,1) and D(2,0).
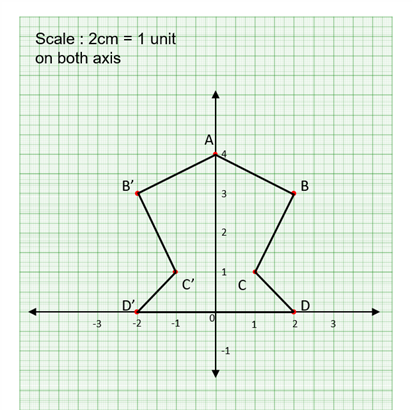
(ii) Reflected points B'(-2,3), C'(-1,1) and D'(-2,0).
(iii) The figure is symmetrical about x = 0
Reflection (In x-axis, y-axis, x=a, y=a and the origin ; Invariant Points) Exercise Ex. 12
Solution 2
(i) (-6, 4)
The co-ordinates of the given point under reflection in the line x = 0 are (6, 4).
(ii) (0, 5)
The co-ordinates of the given point under reflection in the line x = 0 are (0, 5).
(iii) (3, -4)
The co-ordinates of the given point under reflection in the line x = 0 are (-3, -4).
Solution 3
(i) (-3, 0)
The co-ordinates of the given point under reflection in the line y = 0 are (-3, 0).
(ii) (8, -5)
The co-ordinates of the given point under reflection in the line y = 0 are (8, 5).
(iii) (-1, -3)
The co-ordinates of the given point under reflection in the line y = 0 are (-1, 3).
Solution 4
(i) Since, Mx (-4, -5) = (-4, 5)
So, the co-ordinates of P are (-4, -5).
(ii) Co-ordinates of the image of P under reflection in the y-axis are (4, -5).
Solution 5
(i) Since, MO (2, -7) = (-2, 7)
So, the co-ordinates of P are (2, -7).
(ii) Co-ordinates of the image of P under reflection in the x-axis (2, 7).
Solution 6
MO (a, b) = (-a, -b)
My (-a, -b) = (a, -b)
Thus, we get the co-ordinates of the point P' as (a, -b). It is given that the co-ordinates of P' are (4, 6).
On comparing the two points, we get,
a = 4 and b = -6
Solution 7
(i) The reflection in x-axis is given by Mx (x, y) = (x, -y).
A' = reflection of A (-3, 2) in the x- axis = (-3, -2).
The reflection in origin is given by MO (x, y) = (-x, -y).
A'' = reflection of A' (-3, -2) in the origin = (3, 2)
(ii) The reflection in y-axis is given by My (x, y) = (-x, y).
The reflection of A (-3, 2) in y-axis is (3, 2).
Thus, the required single transformation is the reflection of A in the y-axis to the point A''.
Solution 8
(i) Reflection in y-axis is given by My (x, y) = (-x, y)
![]() A' = Reflection of A (2, 6) in y-axis = (-2, 6)
A' = Reflection of A (2, 6) in y-axis = (-2, 6)
Similarly, B' = (3, 5) and C' = (-4, 7)
Reflection in origin is given by MO (x, y) = (-x, -y)
![]() A'' = Reflection of A' (-2, 6) in origin = (2, -6)
A'' = Reflection of A' (-2, 6) in origin = (2, -6)
Similarly, B'' = (-3, -5) and C'' = (4, -7)
(ii) A single transformation which maps triangle ABC to triangle A''B''C'' is reflection in x-axis.
Solution 9
(c)
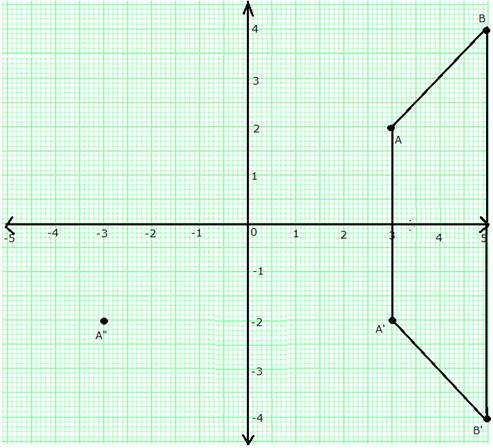
(i) From graph, it is clear that ABB'A' is an isosceles trapezium.
(ii) The measure of angle ABB' is 45°.
(iii) A'' = (-3, -2)
(iv) Single transformation that maps A' to A" is the reflection in y-axis.
Solution 10
(i) We know that every point in a line is invariant under the reflection in the same line.
Since points (3, 0) and (-1, 0) lie on the x-axis.
So, (3, 0) and (-1, 0) are invariant under reflection in x-axis.
Hence, the equation of line L1 is y = 0.
Similarly, (0, -3) and (0, 1) are invariant under reflection in y-axis.
Hence, the equation of line L2 is x = 0.
(ii) P' = Image of P (3, 4) in L1 = (3, -4)
Q' = Image of Q (-5, -2) in L1 = (-5, 2)
(iii) P'' = Image of P (3, 4) in L2 = (-3, 4)
Q'' = Image of Q (-5, -2) in L2 = (5, -2)
(iv) Single transformation that maps P' onto P" is reflection in origin.
Solution 11
(i) We know reflection of a point (x, y) in y-axis is (-x, y).
Hence, the point (-2, 0) when reflected in y-axis is mapped to (2, 0).
And, the point (5, -6) when reflected in y-axis is mapped to (-5, -6).
Thus, the mirror line is the y-axis and its equation is x = 0.
(ii) Co-ordinates of the image of (-8, -5) in the mirror line (i.e., y-axis) are (8, -5).
Solution 12
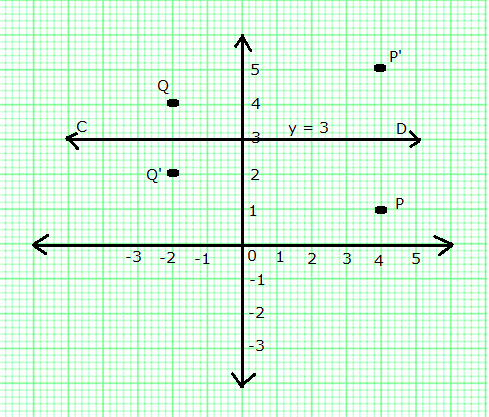
The line y = 3 is a line CD parallel to x-axis and at a distance of 3 units from it.
Mark points P(4, 1) and Q(-2, 4).
Mark P' at the same distance above CD as P is below it. Since, P is 2 units below CD, its image P' will be 2 units above CD.
Hence, the co-ordinates of P' are (4, 5).
Similarly, mark Q' at the same distance below CD as Q is above it. Since, Q is 1 unit above CD, its image Q' will be 1 unit below CD.
Hence, the co-ordinates of Q' are (-2, 2).
Solution 13
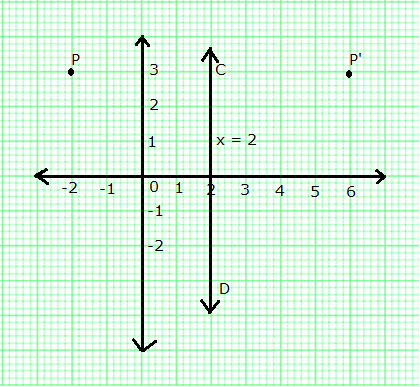
The line x = 2 is a line CD parallel to y-axis and at a distance of 2 units from it.
Mark point P(-2, 3).
Mark P' at the same distance to the right of CD as P is to the left of it.
Hence, the co-ordinates of P' are (6, 3).
Solution 14

A point P (a, b) is reflected in the x-axis to P' (2, -3).
We know Mx (x, y) = (x, -y)
Thus, co-ordinates of P are (2, 3). Hence, a = 2 and b = 3.
P" = Image of P reflected in the y-axis = (-2, 3)
P''' = Reflection of P in the line (x = 4) = (6, 3)
Solution 15

(a) A' = Image of A under reflection in the x-axis = (3, -4)
(b) B' = Image of B under reflection in the line AA' = (6, 2)
(c) A" = Image of A under reflection in the y-axis = (-3, 4)
(d) B" = Image of B under reflection in the line AA" = (0, 6)
Solution 16
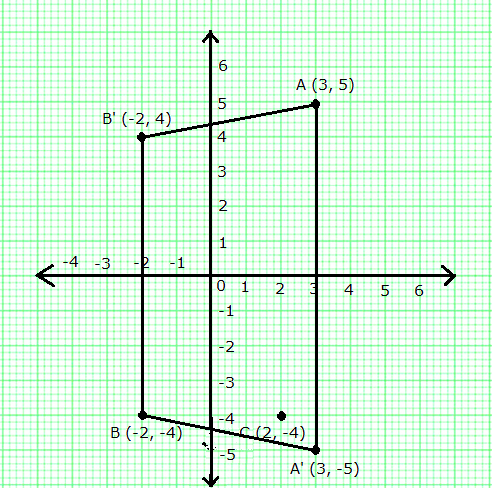
(i) The points A (3, 5) and B (-2, -4) can be plotted on a graph as shown.
(ii) A' = Image of A when reflected in the x-axis = (3, -5)
(iii) C = Image of B when reflected in the y-axis = (2, -4)
B' = Image when C is reflected in the origin = (-2, 4)
(iv) Isosceles trapezium
(v) Any point that remains unaltered under a given transformation is called an invariant.
Thus, the required two points are (3, 0) and (-2, 0).
Solution 17
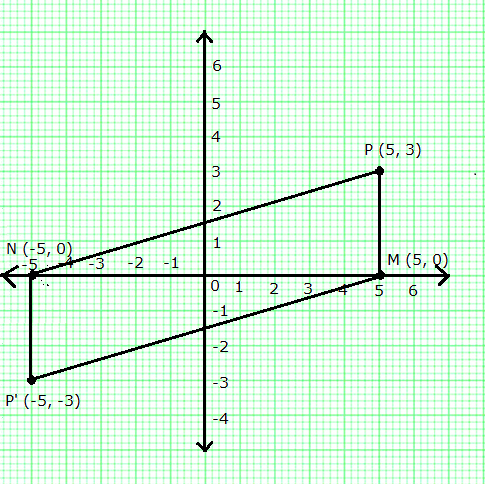
(a) Co-ordinates of P' = (-5, -3)
(b) Co-ordinates of M = (5, 0)
(c) Co-ordinates of N = (-5, 0)
(d) PMP'N is a parallelogram.
(e) Area of PMP'N = 2 (Area of D PMN)
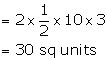
Solution 1(a)
Correct option: (i) on the line l
A point P is its own image in a line l, then point P is on the line l.
Solution 1(b)
Correct option: (ii) (7, 8)
When point P(–7, 8) is reflected in the origin, its coordinates become (7, –8).
It is then reflected in the x-axis to get the point Q.
Therefore, Q ≡ (7, 8).
Solution 1(c)
Correct option: (i) (6, –6)
Let P be (a, b).
When reflected in the y-axis, its coordinates are (–a, b).
Then it is reflected in the origin. So, the coordinates are (a, –b).
But (a, –b) = (6, 6)
i.e. a = 6 & b = –6
The coordinates of P are (6, –6).
Solution 1(d)
Correct option: (iv) (–4, –8)
When x = 0, we get y-axis.
The point P(4, –8) is reflected in the y-axis.
So, the co-ordinates of point R are (–4, –8).
Solution 1(e)
Correct option: (i) (5, 5)
When y = 0, we get x-axis.
Point P(5, 5) is first reflected in the x-axis and so the co-ordinates are (5, –5).
It is then reflected to x-axis to get the point Q.
Therefore, Q ≡ (5, 5).
