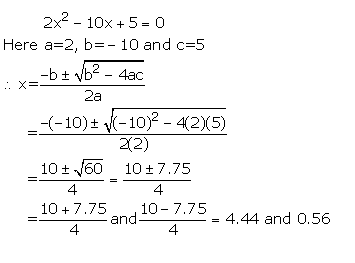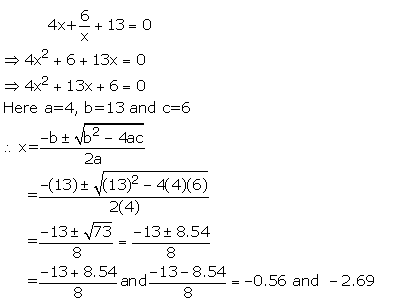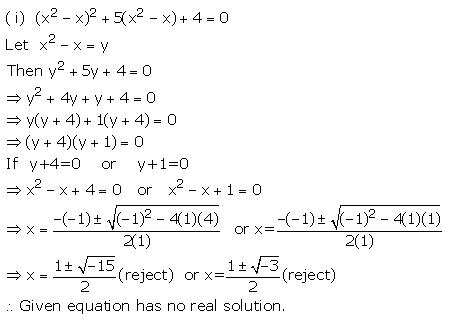Class 10 SELINA Solutions Maths Chapter 5 - Quadratic Equations
Quadratic Equations Exercise Ex. 5(A)
Solution 1(a)
Correct Option: (iv) ![]()
4x2 – 9 = 0
4x2 = 9
![]()
Solution 1(b)
Correct Option: (iii) 3 or –5
(x – 3)(x + 5) = 0
(x – 3) = 0 or (x + 5) = 0
x = 3 or x = –5
Solution 1(c)
Correct Option: (ii) –3
Substituting x = 4 in equation x2 + kx – 4 = 0,
(4)2 + k(4) – 4 = 0
16 + 4k – 4 = 0
4k + 12 = 0
4k = –12
k = –3
Solution 1(d)
Correct Option: (i) –2
Substituting x = 2 in equation 2x2 – 3x + k = 0,
2(2)2 – 3(2) + k = 0
8 – 6 + k = 0
2 + k = 0
k = –2
Solution 1(e)
Correct Option: (iv) 0 or 7
x2 – 7x = 0
x(x – 7) = 0
x = 0 or x – 7 = 0
x = 0 or x = 7
Solution 2(i)
5x2 - 8x = -3(7 - 2x)
⇒ 5x2 - 8x = 6x - 21
⇒ 5x2 - 14x + 21 =0; which is of the form ax2 + bx + c = 0.
∴ Given equation is a quadratic equation.
Solution 2(ii)
(x - 4)(3x + 1) = (3x - 1)(x +2)
⇒ 3x2 + x - 12x - 4 = 3x2 + 6x - x - 2
⇒ 16x + 2 =0; which is not of the form ax2 + bx + c = 0.
∴ Given equation is not a quadratic equation.
Solution 2(iii)
7x3 - 2x2 + 10 = (2x - 5)2
⇒ 7x3 - 2x2 + 10 = 4x2 - 20x + 25
⇒ 7x3 - 6x2 + 20x - 15 = 0; which is not of the form ax2 + bx + c = 0.
∴ Given equation is not a quadratic equation.
Solution 3(i)
x2 - 2x - 15 = 0
For x = 5 to be solution of the given quadratic equation it should satisfy the equation.
So, substituting x = 5 in the given equation, we get
L.H.S = (5)2 - 2(5) - 15
= 25 - 10 - 15
= 0
= R.H.S
Hence, x = 5 is a solution of the quadratic equation x2 - 2x - 15 = 0.
Solution 3(ii)
2x2 - 7x + 9 = 0
For x = -3 to be solution of the given quadratic equation it should satisfy the equation
So, substituting x = 5 in the given equation, we get
L.H.S=2(-3)2 - 7(-3) + 9
= 18 + 21 + 9
= 48
≠ R.H.S
Hence, x = -3 is not a solution of the quadratic equation 2x2 - 7x + 9 = 0.
Solution 4
For x = ![]() to be solution of the given quadratic equation it should satisfy the equation
to be solution of the given quadratic equation it should satisfy the equation
So, substituting x = ![]() in the given equation, we get
in the given equation, we get
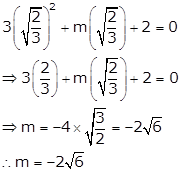
Solution 5
For x = ![]() and x = 1 to be solutions of the given quadratic equation it should satisfy the equation
and x = 1 to be solutions of the given quadratic equation it should satisfy the equation
So, substituting x = ![]() and x = 1 in the given equation, we get
and x = 1 in the given equation, we get
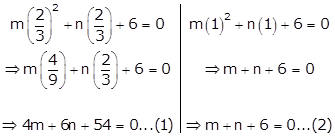
Solving equations (1) and (2) simultaneously,
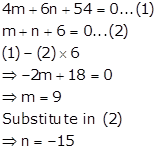
Quadratic Equations Exercise Ex. 5(B)
Solution 1(a)
Correct Option: (iii) –1 or 7
x2 – 6x – 7 = 0
x2 – 7x + x – 7 = 0
x(x – 7) + (x – 7) = 0
(x – 7)(x + 1) = 0
x = 7 or x = –1
Solution 1(b)
Correct Option: (ii) –6 or –2
x(x + 8) + 12 = 0
x2 + 8x + 12 = 0
x2 + 6x + 2x + 12 = 0
x(x + 6) + 2(x + 6) = 0
(x + 6)(x + 2) = 0
x = –6 or x = –2
Solution 1(c)
Correct Option: (ii) 2
Substituting x = 2 in equation (p – 3)x2 + x + p = 0 is 2,
(p – 3)22 + 2 + p = 0
4p – 12 + 2 + p = 0
5p – 10 = 0
p = 2
Solution 1(d)
Correct Option: (iii) 2 or ½
![]()
x2 + 1 = 2.5x
x2 – 2.5x + 1 = 0
x2 – 2x – 0.5x + 1 = 0
x(x – 2) – 0.5(x – 2) = 0
(x – 2)(x – 0.5) = 0
x = 2 or x = 0.5 = ½
Solution 1(e)
Correct Option: (i) x ≠ 0
If x = 0, the term ![]() in the equation will be undefined.
in the equation will be undefined.
Hence, for a quadratic equation ![]() , x ≠ 0.
, x ≠ 0.
Solution 2
![]()

Solution 3
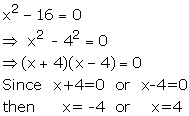
Solution 4
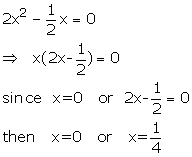
Solution 5
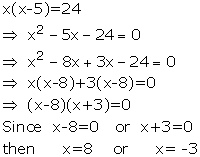
Solution 6
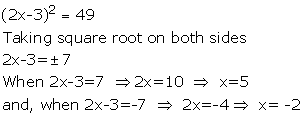
Solution 7

Solution 8
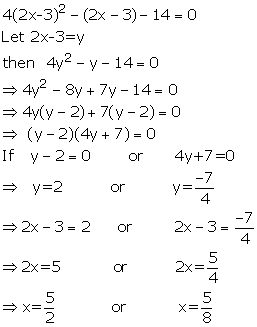
Solution 9
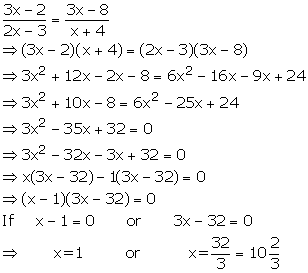
Solution 10
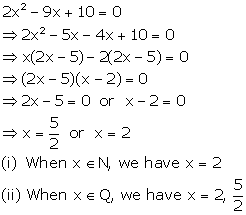
Solution 11
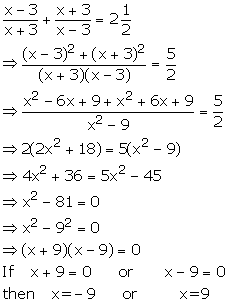
Solution 12
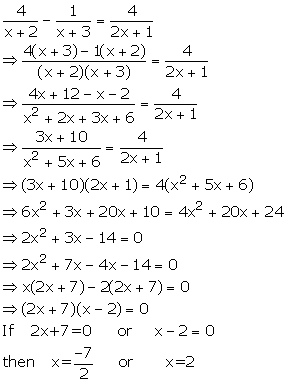
Solution 13
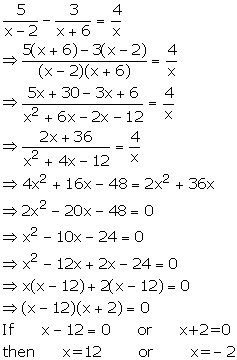
Solution 14

Solution 15


Solution 16(i)
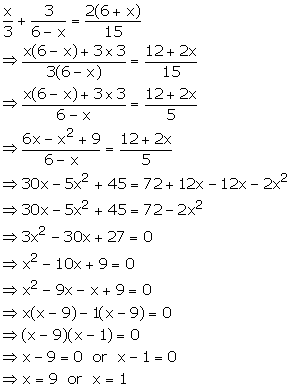
Solution 16(ii)
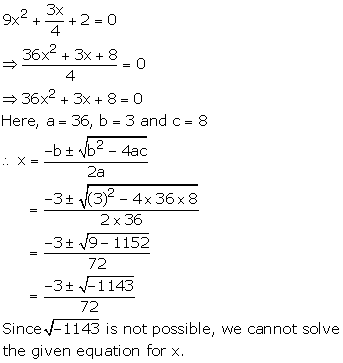
Solution 17
If a + 7 =0, then a = -7
and b + 10 =0, then b = - 10
Put these values of a and b in the given equation
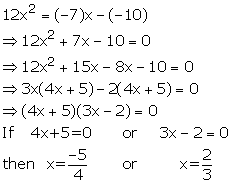
Solution 18
4(2x+3)2 - (2x+3) - 14 =0
Put 2x+3 = y
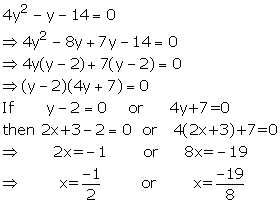
Solution 19
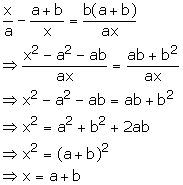
or x = -(a + b)
Solution 20
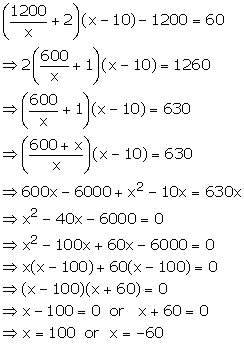
Quadratic Equations Exercise Ex. 5(C)
Solution 1(a)
Correct Option: (ii) 2.0 or 1.0
x2 – 3x + 2 = 0
Then, a = 1, b = –3, c = 2
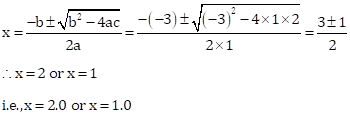
Solution 1(b)
Correct Option: (i) 5.00 or –1.00
x2 – 4x – 5 = 0
Then, a = 1, b = –4, c = –5
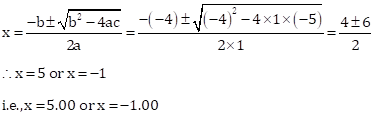
Solution 1(c)
Correct Option: (ii) 9 or –1
x2 – 8x – 9 = 0
Then, a = 1, b = –8, c = –9
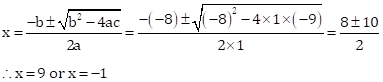
Solution 1(d)
Correct Option: (iii) 3.0 or –1.0
x2 – 2x – 3 = 0
Then, a = 1, b = –2, c = –3
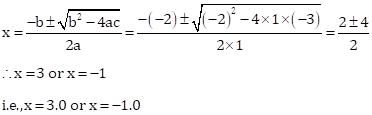
Solution 1(e)
Correct Option: (i) 8 or –2
x2 – 6x – 16 = 0
Then, a = 1, b = –6, c = –16
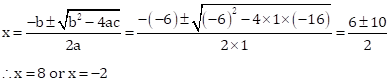
Solution 2
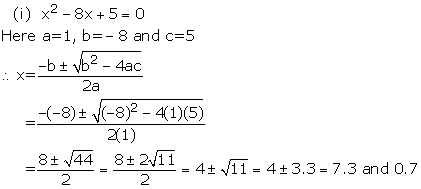
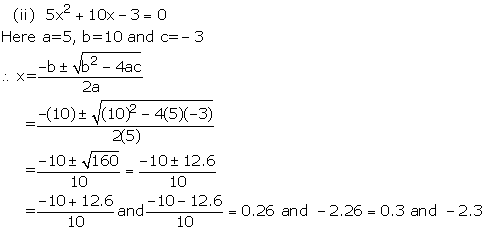
Solution 3(i)
Solution 3(ii)
Solution 3(iii)
4x2 - 5x - 3 = 0
Here, a = 4, b = -5 and c = -3
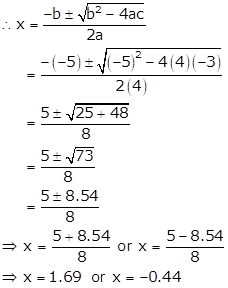
Solution 4
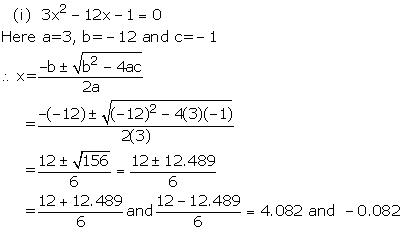
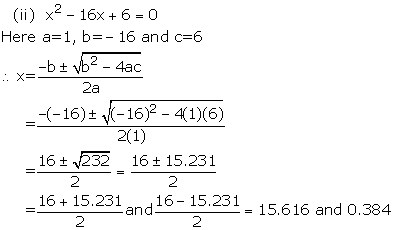
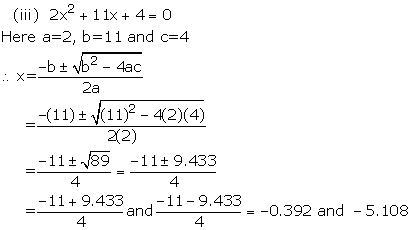
Solution 5
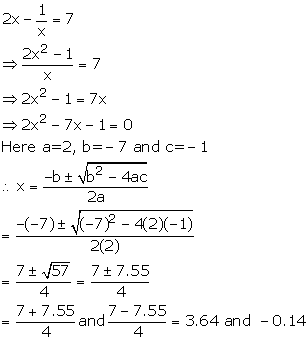
Solution 6
Consider the given equation:
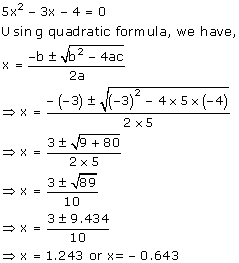
Solution 7
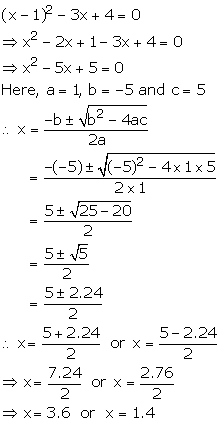
Quadratic Equations Exercise Ex. 5(D)
Solution 1(a)
Correct Option: (i) distinct and real roots
2x2 – 3x + 1 = 0
Here, a = 2, b = –3, c = 1
b2 – 4ac = (–3)2 – 4(2)(1) = 9 – 8 = 1 > 0
Hence, the roots are distinct and real.
Solution 1(b)
Correct Option: (i) x2 – 5x + 6 = 0
For a quadratic equation ax2 + bx + c = 0, the roots are real and distinct if b2 – 4ac > 0.
For, x2 – 5x + 6 = 0
a = 1, b = –5, c = 6
b2 – 4ac = (–5)2 – 4(1)(6) = 25 – 24 = 1 > 0
Hence, the roots are distinct and real.
Solution 1(c)
Correct Option: (iv) 4 or –4
For, x2 – px + 4 = 0, the roots are equal.
Then, b2 – 4ac = 0
Here, a = 1, b = –p, c = 4
b2 – 4ac = 0
(–p)2 – 4(1)(4) = 0
p2 – 16 = 0
p2 = 16
p = ±4
Solution 1(d)
Correct Option: (ii) 2x2 – 5x + 9 = 0
For a quadratic equation ax2 + bx + c = 0, the roots are imaginary if b2 – 4ac < 0.
For, 2x2 – 5x + 9 = 0
a = 2, b = –5, c = 9
b2 – 4ac = (–5)2 – 4(2)(9) = –47 < 0
Hence, the roots are imaginary.
Solution 1(e)
Correct Option: (i) 7
Substituting x = 1 in equation 3x2 – mx + 4 = 0,
3(1)2 – m(1) + 4 = 0
3 – m + 4 = 0
m = 7
Solution 2
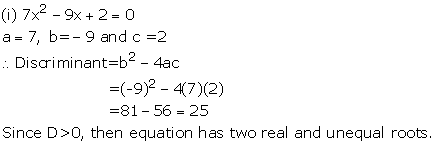
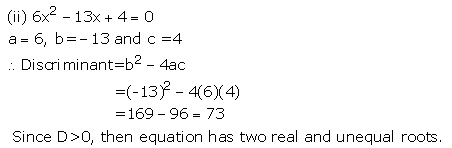
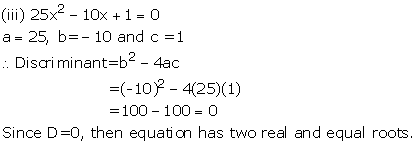
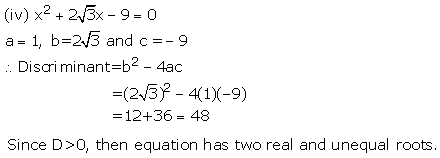
Solution 3
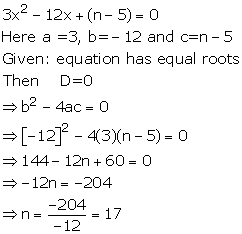
Solution 4
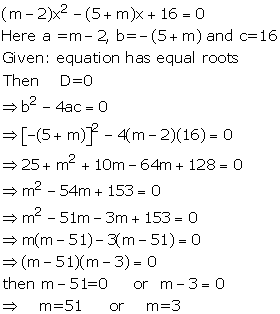
Solution 5
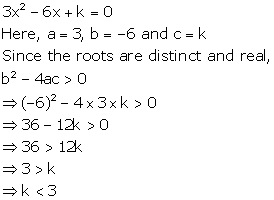
Solution 6
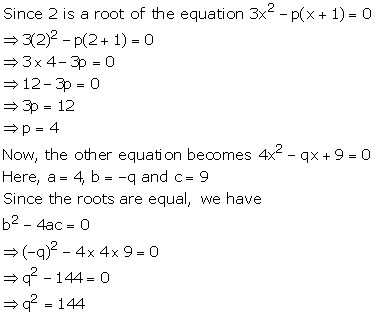
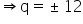
Hence, p = 4 and q = 12 or -12
Quadratic Equations Exercise Ex. 5(E)
Solution 1(a)
Correct Option: (ii) ±1 or ±2
x4 – 5x2 + 4 = 0
Let x2 = y
Then,
y2 – 5y + 4 = 0
y2 – 4y – y + 4 = 0
y(y – 4) – 1(y – 4) = 0
(y – 4)(y – 1) = 0
y = 4 or y = 1
x2 = 4 or x2 = 1
x = ±2 or x = ±1
Solution 1(b)
Correct Option: (ii) 10

20x – 50 = 3x2 – 15x
3x2 – 35x + 50 = 0
3x2 – 30x – 5x + 50 = 0
3x(x – 10) – 5(x – 10) = 0
(x – 10)(3x – 5) = 0
x = 10 or ![]()
Solution 1(c)
Correct Option: (iii) x ≠ 3 and x ≠ –5
![]()
Here, x – 3 ≠ 0 and x + 5 ≠ 0
x ≠ 3 and x ≠ –5
Solution 1(d)
Correct Option: (i) –2 and 9 or –9 and 2
Since the product is negative, one integer should be negative.
From the given options, option (i) satisfies the condition.
Hence, the two integers are –2 and 9 or –9 and 2.
Solution 2
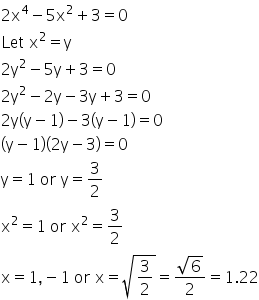
Solution 3
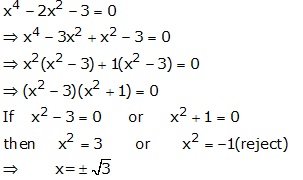
Solution 4 (i)
Solution 4 (ii)
(x2 - 3x)2 - 16(x2 - 3x) - 36 = 0
Let x2 - 3x = y
Then y2 - 16y - 36 = 0
⇒ y2 - 18y + 2y - 36 = 0
⇒ y(y - 18) + 2(y - 18) = 0
⇒ (y - 18) (y + 2) = 0
If y - 18 = 0 or y + 2 = 0
⇒ x2 - 3x - 18 = 0 or x2 - 3x + 2 = 0
⇒ x2 - 6x + 3x - 18 = 0 or x2 - 2x - x + 2 = 0
⇒ x(x - 6) +3(x - 6) = 0 or x(x - 2) -1(x - 2) = 0
⇒ (x - 6) (x + 3) = 0 or (x - 2) (x - 1) = 0
If x - 6 = 0 or x + 3 = 0 or x - 2 = 0 or x - 1 = 0
then x = 6 or x = -3 or x = 2 or x = 1
Solution 5
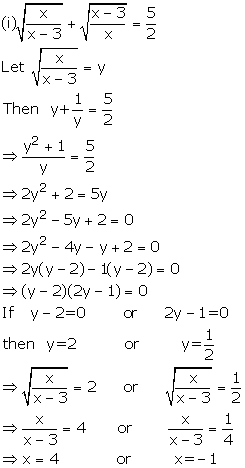
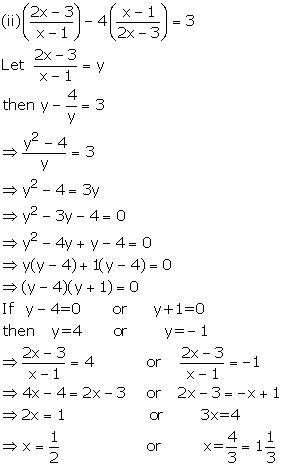
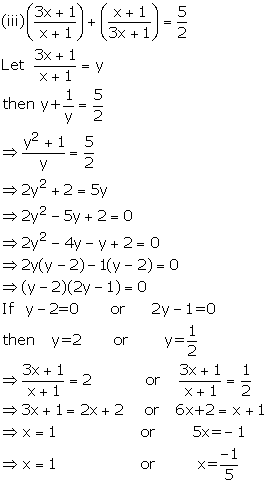
Solution 6

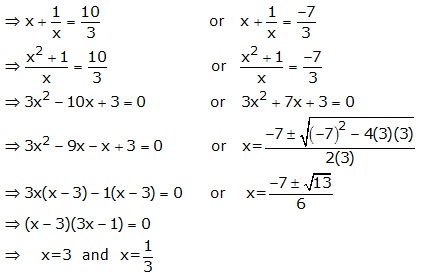
Solution 7

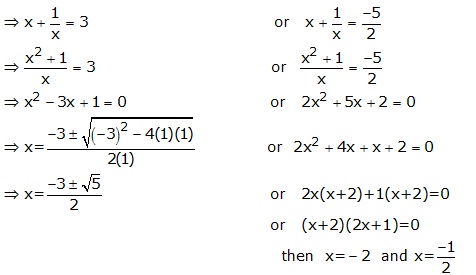
Solution 8

Solution 9
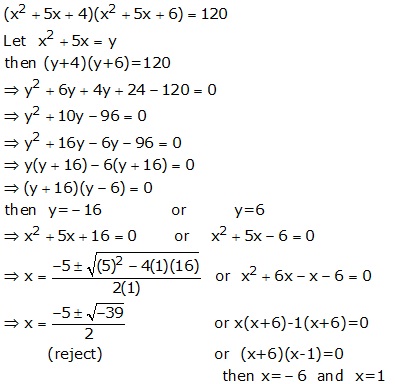
Solution 10
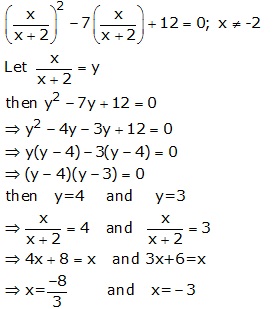
Solution 11
![]()
∴ Given equation reduces to
![]()
⇒ 2y2 - 3 = 5y
⇒ 2y2 - 5y - 3 = 0
⇒ 2y2 - 6y + y - 3 = 0
⇒ 2y(y - 3) + 1(y - 3) = 0
⇒ (y - 3)(2y + 1) = 0
⇒ y = 3 and ![]()
When, y = 3
![]()
⇒ 2x - 1 = 3x + 9
⇒ x = -10
When, ![]()
![]()
⇒ 4x - 2 = -x - 3
![]()
Quadratic Equations Exercise TEST YOURSELF
Solution 1(a)
Correct Option: (ii) –4
Consider (3x – 5)(x + 3)
= 3x2 – 5x + 9x – 15
= 3x2 + 4x – 15
Now, 3x2 – kx – 15 = (3x – 5)(x + 3)
That is 3x2 – kx – 15 = 3x2 + 4x – 15
Therefore, –k = 4 ⇒ k = –4
Solution 1(b)
Correct Option: (ii) 4
For a quadratic equation ax2 + bx + c = 0, the roots are real and equal if b2 – 4ac = 0.
For kx2 + kx + 1 = 0,
a = k, b = k and c = 1
Now, b2 – 4ac = 0
k2 – 4(k)(1) = 0
k2 – 4k = 0
k(k – 4) = 0
k = 0 or k – 4 = 0 ⇒ k = 4
But for k = 0, the given equation is not satisfied.
Hence, k = 4
(k = 4 is obtained by considering the roots of the equation as real and equal and NOT real and distinct)
Solution 1(c)
Correct Option: (iii) 5 or –1
x2 – 4x = 5
x2 – 4x – 5 = 0
x2 – 5x + x – 5 = 0
x(x – 5) + 1(x – 5) = 0
(x – 5)(x + 1) = 0
x = 5 or x = –1
Solution 1(d)
Correct Option: (iv) 0 or 7
x2 – 7x = 0
x(x – 7) = 0
x = 0 or x – 7 = 0
x = 0 or x = 7
Solution 1(e)
Correct Option: (i) 1
Substituting x = 1 in ![]() ,
,

Solution 2
Given ![]() i.e
i.e ![]()
So, the given quadratic equation becomes
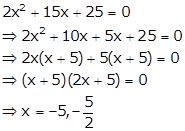
Hence, the values of x are ![]() and
and![]() .
.
Solution 3
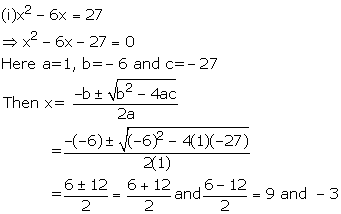
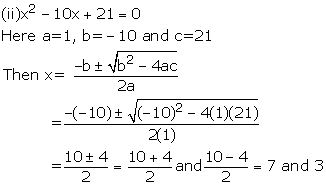
(iii)
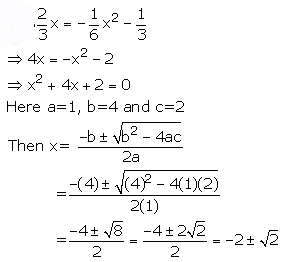
(iv)
(v)
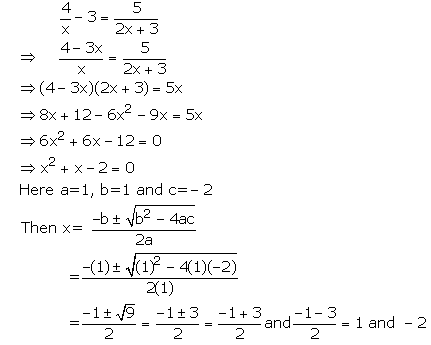
(vi)
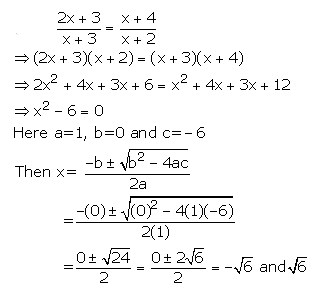
(vii)

(viii)
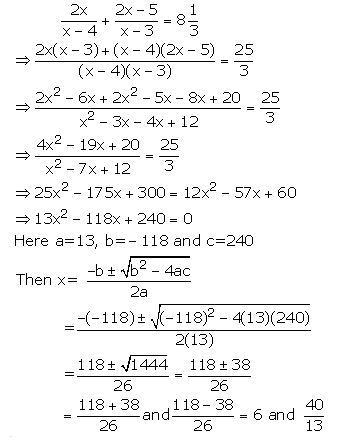
Solution 4
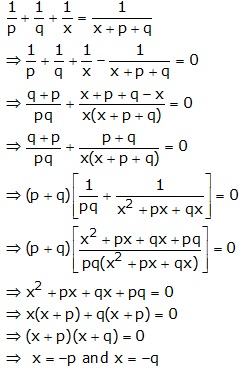
Solution 5
Given quadratic equation is ![]()
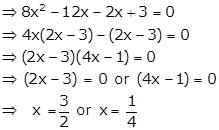
(i) When ![]() the equation
the equation ![]() has no roots
has no roots
(ii) When ![]() the roots of
the roots of ![]() are
are
![]() or
or ![]()
Solution 6
Given quadratic equation is ![]()
Using quadratic formula,
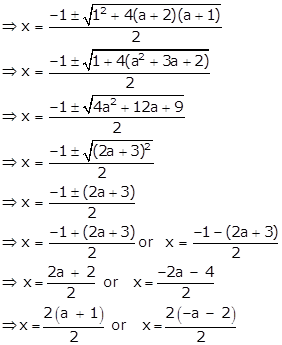
⇒ x = a + 1 or x = -a - 2 = -(a + 2)
Solution 7
Given quadratic equation is ![]()
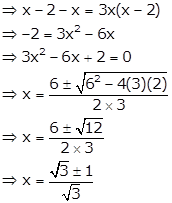
Since, m and n are roots of the equation, we have
![]() and
and ![]()
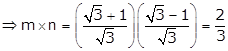
Hence, ![]() .
.
Solution 8
Given quadratic equation is ![]() …. (i)
…. (i)
One of the roots of (i) is ![]() , so it satisfies (i)
, so it satisfies (i)
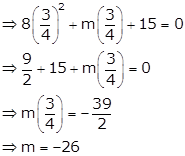
So, the equation (i) becomes ![]()
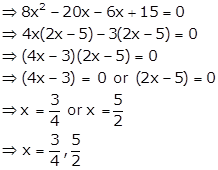
Hence, the other root is![]() .
.
Solution 9
Given quadratic equation is ![]() …. (i)
…. (i)
One of the roots of (i) is -3, so it satisfies (i)
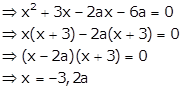
Hence, the other root is 2a.
Solution 10
Given quadratic equation is ![]() ….. (i)
….. (i)
Also, given ![]() and
and ![]()
![]() and
and ![]()
So, the equation (i) becomes
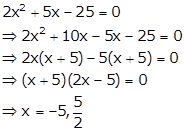
Hence, the solution of given quadratic equation are ![]() and
and![]() .
.
Solution 11
Given quadratic equation is ![]() …. (i)
…. (i)
The quadratic equation has equal roots if its discriminant is zero
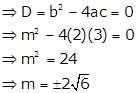
When ![]() , equation (i) becomes
, equation (i) becomes
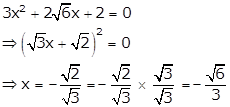
When ![]() , equation (i) becomes
, equation (i) becomes
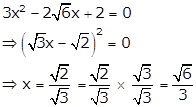
∴ x = ![]()
Solution 12
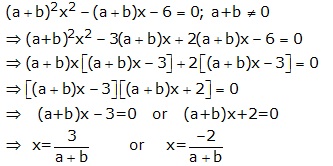
Solution 13
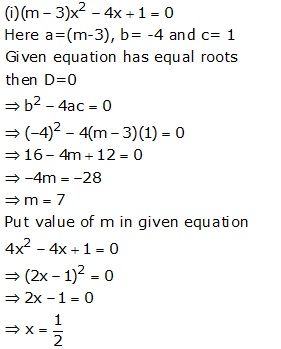
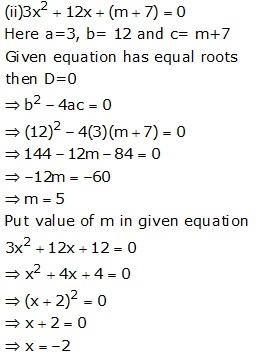
Solution 14
Consider the given equation:

Solution 15
Given quadratic equation is ![]() …. (i)
…. (i)
The quadratic equation has real roots if its discriminant is greater than or equal to zero
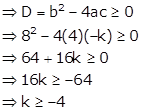
Hence, the given quadratic equation has real roots for![]() .
.
Solution 16
(i) Given quadratic equation is ![]()
D = b2 - 4ac =![]() = 25 - 24 = 1
= 25 - 24 = 1
Since D > 0, the roots of the given quadratic equation are real and distinct.
Using quadratic formula, we have
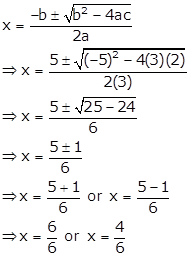
![]() or
or ![]()
(ii) Given quadratic equation is ![]()
D = b2 - 4ac =![]() = 16 - 20 = - 4
= 16 - 20 = - 4
Since D < 0, the roots of the given quadratic equation does not exist.
Solution 17
Since, -2 is a root of the equation 3x2 + 7x + p = 1.
⇒ 3(-2)2 + 7(-2) + p = 1
⇒ 12 - 14 + p = 1
⇒ p = 3
The quadratic equation is x2 + k(4x + k - 1) + p = 0
i.e. x2 + 4kx + k2 - k + 3 = 0
Comparing equation x2 + 4kx + k2 - k + 3 = 0 with ax2 + bx + c = 0, we get
a = 1, b = 4k and c = k2 - k + 3
Since, the roots are equal.
⇒ b2 - 4ac = 0
⇒ (4k)2 - 4(k2 - k + 3) = 0
⇒ 16k2 - 4k2 + 4k - 12 = 0
⇒ 12k2 + 4k - 12 = 0
⇒ 3k2 + k - 3 = 0
By quadratic formula, we have
![]()
![]()