Class 10 SELINA Solutions Maths Chapter 25 - Probability
Probability Exercise Ex. 25(A)
Solution 2
Sample Space = {H, T}
n(S) = 2
(i) A = Event of getting a tail = {T}
n(A)= 1
Therefore, the probability of getting a tail = ![]()
(ii) Not getting a tail
Since P(getting a tail) + P(not getting a tail) = 1
→ P(not getting a tail) = 1 - (1/2) = 1/2
Solution 3
Total number of balls = 3 + 5 + 2 = 10
Total number of possible outcomes = 10
(i) There are 5 black balls
Number of favourable outcomes = 5
Hence, P(getting a black ball) = 5/10 = 1/2
(ii) There are 2 red balls
Number of favourable outcomes = 2
Hence, P(getting a red ball) = 2/10 = 1/5
(iii)
There are 3 white balls
Number of favourable outcomes = 3
Hence, P(getting a white ball) = 3/10 = 3/10
(iv) There are 3 + 5 = 8 balls which are not red
Number of favourable outcomes = 8
Hence, P(getting a white ball) = 8/10 = 4/5
(v) There are 3 + 2 = 5 balls which are not black
Number of favourable outcomes = 5
Hence, P(getting a white ball) = 5/10 = 1/2
Solution 4
Sample space = {1, 2, 3, 4, 5, 6}
n(s) = 6
(i) E = event of getting a number greater than 4 = {5, 6}
n (E) = 2
Probability of getting a number greater than 4 = ![]()
(ii) E=event of getting a number less than or equal to 4={1, 2, 3, 4}
n(E) = 4
Probability of getting a number less than or equal to 4 = ![]()
(iii) E=event of getting a number not greater than 4={1, 2, 3, 4}
n(E) = 4
Probability of getting a number not greater than 4 = ![]()
Solution 5
Total number of cards = 52
Total number of outcomes = 52
There are 13 cards of each type. The cards of heart and diamond are red in colour. Spade and diamond are black. So, there are 26 red cards and 26 black cards.
(i) Number of black cards in a deck = 26
The number of favourable outcomes for the event of drawing a black card = 26
Probability of drawing a black card = 26/52 = 1/2
(ii) Number of red cards in a deck = 26
Therefore, number of non-red(black) cards = 52 - 26 = 26
The number of favourable outcomes for the event of not drawing a red card = 26
Probability of not drawing a red card = 26/52 = 1/2
(iii) Number of red cards in a deck = 26
The number of favourable outcomes for the event of drawing a red card = 26
Probability of drawing a red card =26/52= 1/2
(iv) There are 52 cards in a deck of cards, and 12 of these cards are face cards (4 kings, 4 queens, and 4 jacks).
The number of favourable outcomes for the event of drawing a face card = 12
Probability of drawing a face card =12/52= 3/13
(v) There are 26 red cards in a deck, and 6 of these cards are face cards (2 kings, 2 queens, and 2 jacks).
The number of favourable outcomes for the event of drawing a face card of red color = 6
Probability of drawing a red face card =6/52 = 3/26
Solution 6
(i) Two complementary events, taken together, include all the outcomes for an experiment and the sum of the probabilities of all outcomes is 1.
P(A) + P(B) = 1
(ii) P(A) = 0.46
Let P(B) be the probability of not happening of event A
We know,
P(A) + P(B) = 1
P(B) = 1 - P(A)
P(B) = 1 - 0.46
P(B) = 0.54
Hence the probability of not happening of event A is 0.54
Solution 7
(i) Winning of Geeta is a complementary event to winning of Ritu
Therefore,
P(winning of Ritu) + P(winning of Geeta) = 1
P(winning of Geeta) = 1 - P(winning of Ritu)
P(winning of Geeta) = 1 - 0.73
P(winning of Geeta) = 0.27
(ii) Not winning of Ritu is a complementary event to winning of Ritu
Therefore,
P(winning of Ritu) + P(not winning of Ritu) = 1
P(not winning of Ritu) = 1 - P(winning of Ritu)
P(not winning of Ritu) = 1 - 0.73
P(not winning of Ritu) = 0.27
Solution 8
(i) But if John looses, Mahesh wins
Hence, probability of John losing the race = Probability of Mahesh winning the race since it is a race between these two only
Therefore, P(winning of Mahesh) = 0.54
(ii) P(winning of Mahesh) + P(winning of John) = 1
0.54 + P(winning of John) = 1
P(winning of John) = 1 - 0.54
P(winning of John) = 0.46
Solution 9
(i) The probability of a sure event is 1 i.e. P(E) = 1 where 'E' is the sure event.
Proof: In a sure event n(E) = n(S)
[Since Number of elements in Event 'E' will be equal to the number of element in sample-space.]
By definition of Probability :
P(E) = n (E)/ n (S) = 1
P(E) = 1
(ii) The probability of an impossible event is '0' i.e. P (E) = 0
Proof: Since E has no element, n(E) = 0
From definition of Probability:
P(E) = n (E) / n(S) = 0 / n(S)
P(E) = 0
(iii) The probability of an event lies between '0' and '1'.
i.e. 0![]() P(E)
P(E) ![]() 1.
1.
Proof: Let 'S' be the sample space and 'E' be the event.
Then
0![]() n(E)
n(E)![]() n (S)
n (S)
0 / n(S) ![]() n(E)/ n(S)
n(E)/ n(S)![]() n(S) / n(S)
n(S) / n(S)
or 0 ![]() P(E)
P(E) ![]() 1
1
The number of elements in 'E' can't be less than '0' i.e. negative and greater than the number of elements in S.
Solution 10
Sample space = {1, 2, 3, 4, 5, 6}
n(S) = 6
(i) E = event of getting a 5 on a throw of die = {5}
n(E) = 1
Probability of getting a 5 =P(E) = n(E)/n(S) = 1/6
(ii) There are only six possible outcomes in a single throw of a die. If we want to find probability of 8 to come up, then in that case number of possible or favourable outcome is 0 (zero)
n(E) = 0
Probability of getting a 8 =P(E) = n(E)/n(S)= 0/6 = 0
(iii) If we consider to find the probability of number less than 8, then all six cases are favourable
n(E) = 6
Probability of getting a number less than 8 =P(E) = n(E)/n(S) = 6/6 = 1
(iv) E = event of getting a prime number = {2, 3, 5}
n(E) = 3
Probability of getting a prime number =P(E) = n(E)/n(S) = 3/6 = 1/2
Solution 11
Sample space = {1, 2, 3, 4, 5, 6}
n(S) = 6
(i) E = the possible even numbers = {2, 4, 6}
n(E) = 3
Probability of getting an even number =P(E) = n(E)/n(S) = 3/6 =1/2
(ii) E = the possible numbers between 3 and 8 = {4, 5, 6}
n(E) = 3
Probability of getting a number between 3 and 8 =P(E) = n(E)/n(S) = 3/6= 1/2
(iii) E = the event of getting an even number or a multiple of 3 = {2, 3, 4, 6}
n(E) = 4
Probability of getting an even number or a multiple of 3 =P(E) = 4/6= 2/3
Solution 12
The probability of an event lies between '0' and '1' i.e. 0![]() P(E)
P(E)![]() 1.
1.
(i)
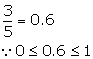
Hence, it can be the probability of an event.
(ii) 2.7
![]()
Hence, it cannot be the probability of an event.
(iii)
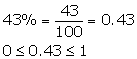
Hence, it can be the probability of an event.
(iv) -0.6
![]()
Hence, it cannot be the probability of an event.
(v) -3.2
![]()
Hence, it cannot be the probability of an event.
(vi) 0.35
![]()
Hence, it can be the probability of an event.
Solution 13
Possible number of outcomes = 6 = number of balls in the bag
n(S) = 6
(i) E = event of drawing a white ball = number of white balls in the bag = 0
n(E) = 0
Probability of drawing a white ball =P(E) = n(E)/n(S)= 0/6 =0
(ii) E = event of drawing a black ball = number of black balls in the bag = 6
n(E) = 6
Probability of drawing a black ball =P(E)= n(E)/n(S)=6/6=1
Solution 14
Possible outcomes = S = {'P', 'r', 'o', 'b', 'a', 'b', 'i', 'l', 'i', 't', 'y'}
n(S) = 11
Event of selection of vowels = E = {'o', 'a', 'i', 'i'}
n(E) = 4
Probability of selection of a vowel = P(E)= n(E)/n(S) = 4/11
Solution 15
Number of possible outcomes = number of days in the month =31
n(S) = 31
(i) E = event of selection of a Wednesday = {1, 8, 15, 22, 29}
n(E) = 5
Probability of selection of a Wednesday =P(E) = n(E)/n(S)= 5/31
(ii) E = event of selection of a Friday = {3, 10, 17, 24, 31}
n(E) = 5
Probability of selection of a Friday =P(E) = n(E)/n(S)=5/31
(iii) E = event of selection of a Tuesday or a Saturday = {4, 7, 11, 14, 18, 21, 25, 28}
n(E) = 8
Probability of selection of a Tuesday or a Saturday =P(E) = n(E)/n(S)= 8/31
Solution 1(a)
Correct option: (iii) P(A) + P(B) = 1
If A and B are two complementary events, then P(A) + P(B) = 1.
Solution 1(b)
Correct option: (iv) ![]()
Possible outcomes are A, E, I, O, U.
Total number of possible outcomes = 5
Number of favourable outcomes = selecting letter ‘O’ = 1
Therefore, the required probability ![]()
Solution 1(c)
Correct option: (iii) ![]()
Possible outcomes when a die is thrown are 1, 2, 3, 4, 5, 6.
Total number of possible outcomes = 6
The even number greater than 4 is 6.
So, the number of favourable outcomes = 1
Therefore, the required probability ![]()
Solution 1(d)
Correct option: (ii) ![]()
Total number of possible outcomes = Total number of English alphabets = 26
The letters of the word ‘DELHI’ are D, E, L, H, I
So, the number of favourable outcomes = 5
Therefore, the required probability ![]()
Solution 1(e)
Correct option: (i) ![]()
Total number of possible outcomes = Total number of cards = 52
Each suit has 3 face cards: King, Queen and Jack.
So, total number of face cards = number of favourable outcomes = 3 × 4 = 12
Therefore, the required probability ![]()
Probability Exercise Ex. 25(B)
Solution 2
There are 9 cards from which one card is drawn.
Total number of elementary events = n(S) = 9
(i) From numbers 2 to 10, there are 5 even numbers i.e. 2, 4, 6, 8, 10
Favorable number of events = n(E) = 5
Probability of selecting a card with an even number = ![]()
(ii) From numbers 2 to 10, there are 3 numbers which are multiples of 3 i.e. 3, 6, 9
Favorable number of events = n(E) = 3
Probability of selecting a card with a multiple of 3=
![]()
(iii) From numbers 2 to 10, there is one number which is an even number as well as multiple of 3 i.e. 6
Favorable number of events = n(E) = 1
Probability of selecting a card with a number which is an even number as well as multiple of 3 = ![]()
(iv) From numbers 2 to 10, there are 7 numbers which are even numbers or a multiple of 3 i.e. 2, 3, 4, 6, 8, 9, 10
Favorable number of events = n(E) = 7
Probability of selecting a card with a number which is an even number or a multiple of 3 = ![]()
Solution 3
There are 100 cards from which one card is drawn.
Total number of elementary events = n(S) = 100
(i) From numbers 1 to 100, there are 20 numbers which are multiple of 5 i.e. {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100} Favorable number of events = n(E) = 20
Probability of selecting a card with a multiple of 5 =
![]()
(ii) From numbers 1 to 100, there are 16 numbers which are multiple of 6 i.e. {6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96} Favorable number of events = n(E) = 16
Probability of selecting a card with a multiple of 6 =
![]()
(iii) From numbers 1 to 100, there are 19 numbers which are between 40 and 60 i.e. {41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59} Favorable number of events = n(E) = 19
Probability of selecting a card between 40 and 60=
![]()
(iv) From numbers 1 to 100, there are 15 numbers which are greater than 85 i.e. {86, 87, …., 98, 99, 100} Favorable number of events = n(E) = 15
Probability of selecting a card with a number greater than 85 =
![]()
(v) From numbers 1 to 100, there are 47 numbers which are less than 48 i.e. {1, 2, ……….., 46, 47} Favorable number of events = n(E) = 47
Probability of selecting a card with a number less than 48 =
![]()
Solution 4
There are 25 cards from which one card is drawn.
Total number of elementary events = n(S) = 25
(i) From numbers 1 to 25, there are 8 numbers which are multiple of 3 i.e. {3, 6, 9, 12, 15, 18, 21, 24} Favorable number of events = n(E) = 8
Probability of selecting a card with a multiple of 3 =
![]()
(ii) From numbers 1 to 25, there are 5 numbers which are multiple of 5 i.e. {5, 10, 15, 20, 25} Favorable number of events = n(E) = 5
Probability of selecting a card with a multiple of 5 =
![]()
(iii) From numbers 1 to 25, there is only one number which is multiple of 3 and 5 i.e. {15} Favorable number of events = n(E) = 1
Probability of selecting a card with a multiple of 3 and 5 =
![]()
(iv) From numbers 1 to 25, there are 12 numbers which are multiple of 3 or 5 i.e. {3, 5, 6, 9, 10, 12, 15, 18, 20,21, 24, 25} Favorable number of events = n(E) = 12
Probability of selecting a card with a multiple of 3 or 5 =
![]()
Solution 5
In throwing a dice, total possible outcomes = {1, 2, 3, 4, 5, 6}
n(S) = 6
(i) On a dice, numbers less than 3 = {1, 2}
n(E) = 2
Probability of getting a number less than 3 = ![]()
(ii) On a dice, numbers greater than or equal to 4 = {4, 5, 6}
n(E) = 3
Probability of getting a number greater than or equal to 4 =
![]()
(iii) On a dice, numbers less than 8 = {1, 2, 3, 4, 5, 6}
n(E) = 6
Probability of getting a number less than 8 = ![]()
(iv) On a dice, numbers greater than 6 = 0
n(E) = 0
Probability of getting a number greater than 6 = ![]()
Solution 6
Number of pages in the book = 85
Number of possible outcomes = n(S) = 85
Out of 85 pages, pages that sum up to 8 = {8, 17, 26, 35, 44, 53, 62, 71, 80}
pages that sum up to 8 = n(E) = 9
Probability of choosing a page with the sum of digits on the page equals 8 = ![]()
Solution 7
In throwing a dice, total possible outcomes = {1, 2, 3, 4, 5, 6}
n(S) = 6
For two dice, n(S) = 6 ![]() 6 = 36
6 = 36
Favorable cases where the sum is 10 or more with 5 on 1st die = {(5, 5), (5, 6)}
Event of getting the sum is 10 or more with 5 on 1st die =n(E) = 2
Probability of getting a sum of 10 or more with 5 on 1st die =
![]()
Solution 8
When two coins are tossed together possible number of outcomes = {HH, TH, HT, TT}
n(S) = 4
(i) E = event of getting both heads = {HH}
n(E) = 1
Probability of getting both heads = ![]()
![]()
(ii) E = event of getting at least one head = {HH, TH, HT}
n(E) = 3
Probability of getting at least one head = ![]()
![]()
(iii) E = event of getting both heads or both tails = {HH, TT}
n(E) = 2
Probability of getting both heads or both tails = ![]()
![]()
Solution 9
In throwing a dice, total possible outcomes = {1, 2, 3, 4, 5, 6}
n(S) = 6
For two dice, n(S) = 6 ![]() 6 = 36
6 = 36
(i) E = event of getting a total of at least 10 = {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)}
n(E) = 6
Probability of getting a total of at least 10 = ![]()
![]()
(ii) E = event of getting a multiple of 2 on one die and an odd number on the other = {(2, 1), (2, 3), (2, 5), (4, 1), (4, 3), (4, 5), (6, 1), (6, 3), (6, 5), (1, 2), (3, 2), (5, 2), (1, 4), (3, 4), (5, 4), (1, 6), (3, 6), (5, 6)}
n(E) = 18
Probability of getting a multiple of 2 on one die and an odd number on the other = ![]()
![]()
Solution 10
Number of possible outcomes when card is drawn from pack of 52 cards = 52
n(S) = 52
(i) Number of spade cards = 13 = E = event of drawing a spade
n(E) = 13
Probability of drawing a spade = ![]()
(ii) Number of red cards(hearts + diamonds) = 26 = E = event of drawing a red card
n(E) = 26
Probability of drawing a red card = ![]()
(iii) Number of face cards(4 kings + 4 queens + 4 Jacks)= 12 = E = Event of drawing a face card
n(E) = 12
Probability of drawing a face card = ![]()
(iv) E = event of drawing a 5 of heart or of diamond = {5H, 5D}
n(E) = 2
Probability of drawing a 5 of heart or of diamond =
![]()
(v) E = event of drawing a jack or a queen = {JH, JS, JD, JC, QH, QS, QD, QC}
n(E) = 8
Probability of drawing a jack or a queen = ![]()
(vi) A card cannot be both an ace as well as a king.
E =event of drawing an ace and a king = 0
n(E) = 0
Probability of drawing an ace and a king = ![]()
(vii) E = event of drawing a red and a king = {KH, KD }
n(E) = 2
Probability of drawing a red and a king =![]()
(viii) E = event of drawing a red or a king = 26 red cards (13 h + 13D) + 2 black kings[since 26 red cards contain 2 red kings]
n(E) = 28
Probability of drawing a red or a king =![]()
Solution 11
Balls in the bag = 16 = Number of balls that could be drawn
n(S) = 16
(i) E = Event of drawing a red ball = number of red balls = 7
n(E) = 7
Probability of drawing a red ball = ![]()
(ii) Not a red ball = 16 - number of red balls = 16 -7 = 9 = E
n(E) = 9
Probability of not drawing a red ball = ![]()
(iii) E = Event of drawing a white ball = number of white balls = 3
n(E) = 3
Probability of drawing a white ball = ![]()
(iv) Not a white ball = 16 - number of white balls = 16-3 = 13=E
n(E) = 13
Probability of not drawing a white ball = ![]()
(v) E = Event of drawing a green or a red ball = number of green balls + number of red balls = 6 + 7 = 13
n(E) = 13
Probability of drawing a green or a red ball = ![]()
(vi) E = Event of drawing a green or a white ball = number of green balls + number of white balls = 6 + 3 = 9
n(E) = 9
Probability of drawing a green or a white ball = ![]()
(vii) E = Event of drawing a green or a white or a red ball = number of green balls + number of white balls + number of red balls = 6 + 3 + 7 = 16
n(E) = 16
Probability of drawing a green or a white or a red ball =
![]()
Solution 12
Total number of balls in the box = 48
Total possible outcomes on drawing a ball = 48
n(S) = 48
(i) Event of drawing a white ball = E = 12
n(E) = 12
Probability of drawing a white ball = ![]()
(ii) Event of drawing a red ball = E = 16
n(E) = 16
Probability of drawing a red ball = ![]()
(iii) Event of drawing a green ball = E = 20
n(E) = 20
Probability of drawing a green ball = ![]()
Probability of not drawing a green ball = 1 - ![]()
![]()
(iv) red or a white ball = 12 + 16 = 28 balls
Event of drawing a red or white ball = E = 28
n(E) = 28
Probability of not drawing a green ball = ![]()
Solution 13
Number of possible outcomes when card is drawn from pack of 52 cards = 52
n(S) = 52
(i) Number of red cards(hearts + diamonds) = 26 = E
n(E) = 26
Probability of drawing a red card = ![]()
(ii) Number of black cards(spade + clubs) = 26 = E
n(E) = 26
Probability of drawing a black card = ![]()
(iii) Number of spade cards = 13 = E = event of drawing a spade
n(E) = 13
Probability of drawing a spade = ![]()
(iv) Number of ace cards = 4 = E = event of drawing an ace
n(E) = 4
Probability of drawing an ace = ![]()
(v) Number of black ace cards = 2 = E = event of drawing an ace
n(E) = 2
Probability of drawing a black ace = ![]()
(vi) There is only one ace of diamonds.
E = event of drawing an ace of diamonds
n(E) = 1
Probability of drawing an ace of diamonds = ![]()
(vii) Number of club cards = 13 = E = event of drawing a club card
n(E) = 13
Probability of drawing a club card = ![]()
Probability of not drawing a club card = 1 - ![]()
![]()
(viii) E = event of drawing a jack or a queen = {JH, JS, JD, JC, QH, QS, QD, QC}
n(E) = 8
Probability of drawing a jack or a queen = ![]()
Solution 14
There are 30 cards from which one card is drawn.
Total number of elementary events = n(S) = 30
(i) From numbers 1 to 30, there are 10 numbers which are multiple of 4 or 6 i.e. {4, 6, 8, 12, 16, 18, 20, 24, 28, 30} Favorable number of events = n(E) = 10
Probability of selecting a card with a multiple of 4 or 6 =
![]()
(ii) From numbers 1 to 30, there are 2 numbers which are multiple of 3 and 5 i.e. {15, 30} Favorable number of events = n(E) = 2
Probability of selecting a card with a multiple of 3 and 5 =
![]()
(iii) From numbers 1 to 30, there are 14 numbers which is multiple of 3 or 5 i.e. {3, 5, 6, 9, 10, 12, 15, 18, 20, 21, 24, 25, 27, 30} Favorable number of events = n(E) = 14
Probability of selecting a card with a multiple of 3 or 5 =
![]()
Solution 15
The number of possible outcomes is 6 × 6 = 36. We write them as given below :
{(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1)
(1, 2), (2, 2), (3, 2), (4, 2), (5, 2), (6, 2)
(1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (6, 3)
(1, 4), (2, 4), (3, 4), (4, 4), (5, 4), (6, 4)
(1, 5), (2, 5), (3, 5), (4, 5), (5, 5), (6, 5)
(1, 6), (2, 6), (3, 6), (4, 6), (5, 6), (6, 6)}
n(S) = 36
(i) E = Event of getting a doublet = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
n(E) = 6
Probability of getting a doublet = ![]()
(ii) E = Event of getting a number less than 3 on each dice
= {(1, 1), (1, 2), (2, 1), (2, 2)}
n(E) = 4
Probability of getting a number less than 3 on each dice = ![]()
(iii) E = Event of getting an odd number as a sum = {(1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (3, 6), (4, 1), (4, 3), (4, 5), (5, 2), (5, 4), (5, 6), (6, 1), (6, 3), (6, 5)}
n(E) = 18
Probability of getting an odd number as sum = ![]()
(iv) E = Event of getting a total of at most 10 =
{(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)
(3,1), (3,2), (3,3), (3,4), (3,5) ,(3,6)
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6)
(5,1), (5,2),(5,3), (5,4), (5,5)
(6,1), (6,2), (6,3), (6,4)}
Therefore total number of favorable ways = 33 = n(E)
Probability of getting a total of at most 10 = ![]()
(v) E = Event of getting an odd number on dice 1 and a number less than or equal to 4 on dice 2 =
{(1,1), (1,2), (1,3), (1,4), (1, 5)
(2, 1), (2, 3), (2, 5)
(3,1), (3,2), (3,3), (3,4), (3, 5)
(4, 1), (4, 3), (4, 5)
(5,1), (5,2),(5,3), (5,4)}
Therefore total number of favorable ways = 20 = n(E)
Probability of getting an odd number on dice 1 and a number less than or equal to 4 on dice 2 = ![]()
Solution 1(a)
Correct option: (ii) 0
A selected card from a pack of 52 cards can be either a king or a jack; it cannot be both.
Hence, such an event does not exist.
Therefore, the probability of the card drawn to be king and jack is 0.
Solution 1(b)
Correct option: (ii) ![]()
A non-leap year has 52 weeks and 1 day.
Now, 52 weeks will have 52 Sundays.
The remaining one day can be either Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, or Saturday.
So, total outcomes = 7
And, favourable outcomes = Sunday = 1
Hence, the required probability ![]()
Solution 1(c)
Correct option: (i) 340
Total articles = 800
Let the number of rejected articles = x
Probability of rejecting an article = 0.425
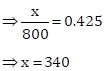
Solution 1(d)
Correct option: (i) 0.5
Total number of balls = 24
Number of favourable outcomes = Number of blue balls = 24 – 4 – 8 = 12
Therefore, the probability of getting a blue ball![]()
Solution 1(e)
Correct option: (ii) ![]()
Total number of integers between 0 and 51 = 50
Integers divisible by 6: 6, 12, 18, 24, 30, 36, 42, 48
Number of favourable outcomes = 8
Therefore, the required probability ![]()
Probability Exercise TEST YOURSELF
Solution 2
Total number of possible outcomes = 52
n(S) = 52
(i) No. of face cards in a deck of 52 cards = 12 (4 kings, 4 queens and 4 jacks)
Event of drawing a face cards = E = (4 kings, 4 queens and 4 jacks)
n(E) = 12
Probability of drawing a face card = ![]()
(ii) Probability of not drawing a face card = 1 - probability of drawing a face card
Probability of not drawing a face card = 1 -![]()
![]()
(iii) Event of drawing a queen of black color ={ Q(spade), Q(club)} = E
n(E) = 2
Probability of drawing a queen of black color =
![]()
(iv) Event of drawing a card with number 5 or 6 = E = {5H, 5D, 5S, 5C, 6H, 6D, 6S, 6C}
n(E) = 8
Probability of drawing a card with number 5 or 6 =
![]()
(v) Numbers less than 8 = { 2, 3, 4, 5, 6, 7}
Event of drawing a card with number less than 8 = E = {6H cards, 6D cards, 6S cards, 6C cards}
n(E) = 24
Probability of drawing a card with number less than 8 =
![]()
(vi) Number between 2 and 9 = {3, 4, 5, 6, 7, 8}
Event of drawing a card with number between 2 and 9 = E = {6H cards, 6D cards, 6S cards, 6C cards}
n(E) = 24
Probability of drawing a card with number between 2 and 9 =
![]()
Solution 3
(i) Probability of winning of A + Probability of losing of A = 1
Probability of losing of A = Probability of winning of B
Therefore,
Probability of winning of A + Probability of winning of B = 1
0.83 + Probability of winning of B = 1
Probability of winning of B = 1 - 0.83 = 0.17
(ii) Probability of winning of B + Probability of losing of B = 1
Probability of losing of B = Probability of winning of A
Therefore,
Probability of winning of A = 0.49
Solution 4
Out of the two friends, A's birthday can be any day of the
year. Now, B's birthday can also be any day of 365 days in the year.
We assume that these 365 outcomes are equally likely.
(i) If A's birthday is different from B's, the number of favourable outcomes for his birthday is 365 - 1 = 364
So, P (A's birthday is different from B's birthday) = ![]()
(ii) P( A and B have the same birthday)
= 1 - P (both have different birthdays)
= 1 - ![]() [Using P( E' ) = 1 - P(E)]
[Using P( E' ) = 1 - P(E)]
= ![]()
Solution 5
When two coins are tossed simultaneously, the possible outcomes are {(H, H), (H, T), (T, H), (T, T)}
n(S) = 4
(i) The outcomes favourable to the event E, 'at least one head' are
{(H, H), (H, T), (T, H)}
So, the number of outcomes favourable to E is 3 = n(E)
Therefore, P(E) = ![]()
(ii) The outcomes favourable to the event E, 'at most one head'
are {(T, H), (H, T), (T, T)}
So, the number of outcomes favourable to E is 3 = n(E)
Therefore, P(E) = ![]()
Solution 6
Total number of cards = 52
3 face cards of spades are removed
Remaining cards = 52 - 3 = 49 = number of possible outcomes
n(S) = 49
(i) Number of black face cards left = 3 face cards of club
Event of drawing a black face card = E = 3
n(E) = 3
Probability of drawing a black face card = ![]()
(ii) Number of queen cards left = 3
Event of drawing a black face card = E = 3
n(E) = 3
Probability of drawing a queen card = ![]()
(iii) Number of black cards left = 23 cards (13 club + 10 spade)
Event of drawing a black card = E = 23
n(E) = 23
Probability of drawing a black card = ![]()
Solution 7
Total result = 0 sec to 40 sec
Total possible outcomes = 40
n(S) = 40
Favorable results = 0 sec to 15 sec
Favorable outcomes = 15
n(E) = 15
Probability that the music will stop in first 15 sec = ![]()
Solution 8
Total number of shirts = 50
Total number of elementary events = 50 = n(S)
(i) Since trader accepts only good shirts and number of good shirts = 44
Event of accepting good shirts = 44 = n(E)
Probability of accepting a good shirt = ![]()
(ii) Since trader rejects shirts with major defects only and number of shirts with major defects = 2
Event of accepting shirts = 50 - 2 = 48 = n(E)
Probability of accepting shirts = ![]()
Solution 9
The number of possible outcomes = 6 × 6 = 36.
(i) The outcomes favourable to the event 'the sum of the two numbers is 8' = E ={(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)}
The number of outcomes favourable to E = n(E) = 5.
Hence, P(E) = ![]()
(ii) There is no outcome favourable to the event E = 'the sum of two numbers is 13'.
n(E) = 0
Hence, P(E) = ![]()
(iii) All the outcomes are favourable to the event E = 'sum of two numbers ![]() 12'.
12'.
Hence, P(E) = ![]()
Solution 10
P(do not have the same birthday)+P(have same birthday)=1
0.897 + P(have same birthday) = 1
P(have same birthday) = 1 - 0.897
P(have same birthday) = 0.103
Solution 11
Total number of possible outcomes = 10+16+8 = 34 balls
n(S) = 34
(i) Favorable outcomes for not a red ball = favorable outcomes for white or green ball
Number of favorable outcomes for white or green ball = 16+8=24 = n(E)
Probability for not drawing a red ball = ![]()
(ii) Favorable outcomes for neither a red nor a green ball = favorable outcomes for white ball
Number of favorable outcomes for white ball = 16 = n(E)
Probability for not drawing a red or green ball = ![]()
(iii) Number of favorable outcomes for white or green ball = 16+8=24 = n(E)
Probability for drawing a white or green ball = ![]()
Solution 12
Total number of coins = 20+50+30 = 100
Total possible outcomes = 100 = n(S)
(i) Number of favorable outcomes for Re 1 coins = 30 = n(E)
Probability(Re 1 coin) = ![]()
(ii) Number of favorable outcomes for not a Rs 2 coins = number of favorable outcomes for Re 1 or Rs 5 coins = 30+20 = 50 = n(E)
Probability(not Rs 2 coin) = ![]()
(iii) number of favorable outcomes for neither Re 1 nor Rs 5 coins = Number of favorable outcomes for Rs 2 coins = 50 = n(E)
Probability(neither Re 1 nor Rs 5 coin) = ![]()
Solution 13
Total number of possible outcomes = 12
(i) Number of favorable outcomes for 6 = 1
P(the pointer will point at 6) = ![]()
(ii) Favorable outcomes for an even number are 2, 4, 6, 8, 10, 12
Number of favorable outcomes = 6
P(the pointer will be at an even number) = ![]()
(iii) Favorable outcomes for a prime number are 2, 3, 5, 7, 11
Number of favorable outcomes = 5
P(the pointer will be at a prime number) = ![]()
(iv) Favorable outcomes for a number greater than 8 are 9, 10, 11, 12
Number of favorable outcomes = 4
P(the pointer will be at a number greater than 8) = ![]()
(v) Favorable outcomes for a number less than or equal to 9 are 1, 2, 3, 4, 5, 6, 7, 8, 9
Number of favorable outcomes = 9
P(the pointer will be at a number less than or equal to 9) =
![]()
(vi) Favorable outcomes for a number between 3 and 11 are 4, 5, 6, 7, 8, 9, 10
Number of favorable outcomes = 7
P(the pointer will be at a number between 3 and 11) = ![]()
Solution 14
Total possible outcomes = 52
(i) Number queens of red color = 2
Number of favorable outcomes = 2
P(queen of red color) = ![]()
(ii) Number of black cards = 26
Number of black face cards = 6
Number of favorable outcomes = 6
P(black face card) = ![]()
(iii) Favorable outcomes for jack or queen of hearts = 1 jack + 1 queen
Number of favorable outcomes = 2
P(jack or queen of hearts) = ![]()
(iv) Number of favorable outcomes for a diamond = 13
Number of favorable outcomes = 13
P(getting a diamond) = ![]()
(v) Number of favorable outcomes for a diamond or a spade = 13 + 13 = 26
Number of favorable outcomes = 26
P(getting a diamond or a spade) = ![]()
Solution 15
There are 12 face cards in a deck.
Therefore, possible number of outcomes = 52 - 12 = 40
(i) number of favorable outcomes for black cards = 26 cards - 6 face cards = 20
P(a black card) = ![]()
(ii) number of favorable outcomes for 8 of red color = 2
P(getting a card with 8 of red color) = ![]()
(iii) Since all face cards are removed
Number of favorable outcomes for a king of black color = 0
P(getting a king of black color) = ![]()
Solution 16
Total number of possible outcomes = 7
(i) Number of favorable outcomes for the card is 8 or the king = 2
P(card is 8 or the king) = ![]()
(ii) a) If a king is drawn and put aside, then total possible outcomes = 6
Number of favorable outcomes for an ace = 1
P(card is an ace) = ![]()
b) Now, for second pick number of king = 0
Number of favorable outcomes for a king = 0
P(card is a king) = ![]()
Solution 17
(i) Total number of pens = 4 + 16 = 20
Total possible outcomes = 20
Number of defective pens = 4
P(defective pen) = ![]()
(ii) If defective pen drawn in first draw is not replaced, total possible outcomes = 20 - 1 = 19
a) Number of defective pens = 3
P(defective pens) = ![]()
b) Number of not defective pens = 16
P(not defective pens) = ![]()
Solution 18
Total number of possible outcomes = 100
(i) Numbers which are perfect squares = 1, 4, 9, 16, 25, 36, 49, 64, 81, 100
Number of favorable outcomes = 10
P(a perfect square) = ![]()
(ii) Numbers which are divisible by 4 = 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96, 100
Number of favorable outcomes = 25
P(number divisible by 4) = ![]()
(iii) Numbers which are divisible by 5 = 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100
Number of favorable outcomes = 20
P(number divisible by 5) = ![]()
(iv) Numbers which are divisible by 4 or 5 = 4, 5, 8, 10, 12, 15, 16, 20, 24, 25, 28, 30, 32, 35, 36, 40, 44, 45, 48, 50, 52, 55, 56, 60, 64, 65, 68, 70, 72, 75, 76, 80, 84, 85, 88, 90, 92, 95, 96, 100
Number of favorable outcomes = 40
P(number divisible by 4 or 5) = ![]()
(v) Numbers which are divisible by 4 and 5 = 20, 40, 60, 80, 100
Number of favorable outcomes = 5
P(number divisible by 4 and 5) = ![]()
Solution 19
Diameter of the circle = 20 cm
Radius = 10 cm
Area of circle = ![]()
Length of paper = 40 cm
Width of paper = 30 cm
Area of paper = 1200 cm2
Total possible outcomes = area of rectangular paper
(i) Since paper is kept on table top and die falls and lands on paper.
Number of favorable outcomes = area of circle.
P(inside the circle) = 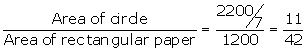
(ii) P(outside the circle) = 1 - P(inside the circle)
= 1 - ![]()
![]()
Solution 20
When two dice are rolled, total number of possible outcomes = 36
(i) Favorable outcomes for the sum of numbers 4 or 5 are:
{(1, 3), (1, 4), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1)}
Number of favorable outcomes = 7
P(getting a sum of 4 or 5) = ![]()
(ii) Favorable outcomes for the sum of numbers 7, 8 or 9 are:
{(1, 6), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 3), (4, 4), (4, 5), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2), (6, 3)}
Number of favorable outcomes = 15
P(getting a sum of 7, 8 or 9) = ![]()
(iii) Favorable outcomes for the sum of numbers between 5 and 8 i.e. 6 or 7 are:
{(1, 5), (1, 6), (2, 4), (2, 5), (3, 3), (3, 4), (4, 2), (4, 3), (5, 1), (5, 2), (6, 1)}
Number of favorable outcomes = 11
P(getting a sum of 6 or 7) = ![]()
(iv) Favorable outcomes for the sum of numbers more than 10 i.e. 11 or 12 are:
{(5, 6), (6, 5), (6, 6)}
Number of favorable outcomes = 3
P(getting a sum of numbers more than 10) = ![]()
(v) Favorable outcomes for the sum of numbers less than 6 I.e. 2, 3, 4 or 5 are:
{(1,1 ), (1, 2), (1, 3), (1, 4), (2,1 ), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1)}
Number of favorable outcomes = 10
P(getting a sum of less than 6) = ![]()
Solution 21
When three coins are tossed, possible outcomes are:
HHH, HHT, HTH, HTT, THH, THT, TTH, TTT
Total possible outcomes = 8
(i) Favorable outcomes for exactly two heads = HHT, THH, HTH
Number of favorable outcomes = 3
P(exactly two heads) = ![]()
(ii) Favorable outcomes for at least two heads = HHT, THH, HTH, HHH
Number of favorable outcomes = 4
P(at least two heads) = ![]()
(iii) Favorable outcomes for at most two heads = HHT, THH, HTH, HTT, THT, TTH, TTT
Number of favorable outcomes = 7
P(at most two heads) = ![]()
(iv) Favorable outcomes for all tails = TTT
Number of favorable outcomes = 1
P(all tails) = ![]()
(v) Favorable outcomes for at least one tails = HHT, THH, HTH, HTT, THT, TTH, TTT
Number of favorable outcomes = 7
P(at least one tail) = ![]()
Solution 22
When two dice are thrown, total possible outcomes = 36
(i) Favorable outcomes for 4 will not come up either time:
{(1,1), (1,2), (1,3), (1,5), (1,6)
(2,1), (2,2), (2,3), (2,5), (2,6)
(3,1), (3,2), (3,3), (3,5), (3,6)
(5,1), (5,2), (5,3), (5,5), (5,6)
(6,1), (6,2), (6,3), (6,5), (6,6)}
Number of favorable outcomes = 25
P(4 will not come up) = ![]()
(ii) P(4 will come up once) = 1 - P(4 will not come up either time)
P(4 will come up once) = 1 - ![]()
P(4 will come up once) = ![]()
Solution 23
Total number of possible outcomes = 5 x 5 = 25
The possible outcomes are:
MM, MT, MW, MTh, MF, TM, TT, TW, TTh, TF, WM, WT, WW, WTh, WF, ThM, ThT, ThW, ThTh, ThF, FM, FT, FW, FTh, FF
(i) Favorable outcomes for two employees remaining absent on same day are: MM, TT, WW, ThTh, FF
Number of favorable outcomes = 5
P(same day) = ![]()
(ii) Favorable outcomes for two employees remaining absent on consecutive days : MT, TM, TW, WT, WTh, ThW, ThF, FTh
Number of favorable outcomes = 8
P(consecutive days) = ![]()
(iii) P(absent on diff days) = 1 - P(absent on same days)

Solution 24
Let the number of black balls in the box be x
Total number of balls in the box = x+30
P(drawing a black ball) = ![]()
P(drawing a white ball = ![]()
But, P(drawing a black ball) = ![]() P(drawing a white ball)
P(drawing a white ball)

Number of black balls in the box = 12
Solution 25
No. of total cards = 52
Cards removed of 4 colours of multiples of 3
= 3, 6, 9 = 4 × 3 = 12
Remaining cards = 52 - 12 = 40
(i)No. of face cards = 12 cards
![]()
![]()
(ii)An even number red cards = 2,4,8,10 cards = 2×4 = 8
![]()
![]()
Solution 26

Solution 27
Here, Total number of all possible outcomes = 16
i. a, e, i and o are the vowels.
Number of favourable outcomes = 4
∴ Required Probability = ![]()
ii. Number of consonants = 16 - 4 (vowels) = 12
∴ Number of favourable outcomes = 12
∴ Required Probability = ![]()
iii. Median contains 6 letters.
∴ Number of favourable outcomes = 16 - 6 = 10
∴ Required Probability = ![]()
Solution 28
A box contains,
60% balls, letter A is marked.
30% balls, letter B is marked.
10% balls, letter C is marked.
i. Total number of all possible outcomes = 100
Number of favourable outcomes = 10
∴ Required Probability =![]()
ii.
The probability that the ball drawn is marked A = ![]() … (1)
… (1)
The probability that the ball drawn is marked B = ![]() … (2)
… (2)
∴ Required Probability = ![]()
iii. The probability that the ball drawn is neither B nor C
= 1 - [P(B) + P(C)]
= 1 - ![]()
= 1 - ![]()
= ![]()
= ![]()
Solution 29
P(C) = 1 - [P(A) + P(B)]![]()
Probability = ![]()
Given that 40 balls in the box are marked C.
⇒ ![]() =
= ![]()
⇒ Total number of all possible outcomes = ![]()
∴ the number of balls in the box is 96.
Solution 1(a)
Correct option: (i) ![]()
When three coins are tossed simultaneously, the possible outcomes are as follows:
HHH, HTH, HHT, THH, THT, TTH, HTT, TTT
⇒ Total number of outcomes = 8
Outcomes with at least two heads: HHH, HTH, HHT, THH
⇒ Total number of favourable outcomes = 4
Therefore, the required probability ![]()
Solution 1(b)
Correct option: (ii) ![]()
Total number of cards = 52
Number of king cards = 4
Number of queen cards = 4
So, total number of favourable outcomes = 4 + 4 = 8
Therefore, the required probability ![]()
Solution 1(c)
Correct option: (iv) Event C
A die contains numbers 1, 2, 3, 4, 5, 6.
Event C: P is 35
35 = 5 × 7
Since the number 7 is not on a die, the probability of getting the product as 35 is 0.
Solution 1(d)
Correct option: (iii) ![]()
Total number of balls = 20 + 12 + 8 = 40
Number of green balls = 8
Therefore, the required probability ![]()
Solution 1(e)
Correct option: (i) Event A
The probability of any event can never be less than 0 or more than 1.
Hence, P(A): ![]() is possible.
is possible.

