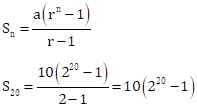Class 10 SELINA Solutions Maths Chapter 11 - Geometric Progression
Geometric Progression Exercise TEST YOURSELF
Solution 10
![]() are three consecutive terms of a G.P.
are three consecutive terms of a G.P.
Then,
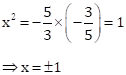
Hence, the value of x is either 1 or –1.
Solution 9
Let the first term = a and the common ratio = r
nth term = arn-1
4th term = 48
⇒ ar3 = 48
And, 7th term = 384
⇒ ar6 = 384
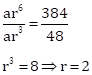
a(2)3 = 48 ⇒ a = 6
Therefore, 6th term = ar5
= 6(2)5
= 192
Solution 8
Let the first term = a and the common ratio, r = 2
nth term = arn-1
10th term = 768
⇒ ar9 = 768
⇒ a(2)9 = 768
⇒ a × 512 = 768
![]()
Therefore, 8th term = ar7
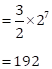
Solution 7
Given G.P. is ![]()
Here, first term, a = 2 and the common ratio, r = ![]()
Let the nth term = ![]()
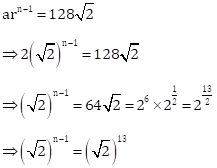
⇒ n – 1 = 13
⇒ n = 14
Solution 6
Let the first term = a and the common ratio = r
nth term = arn-1
10th term = ar9 = x
16th term = ar15 = y
22nd term = ar21 = z
Now,
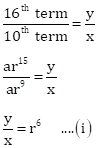
And,

From (i) and (ii),
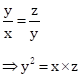
Therefore, x, y and z are in G.P.
Solution 5
Let the first term = a and the common ratio = r
3rd term = ar2 = 2
Product of first five terms
= ar0 × ar1 × ar2 × ar3 × ar4
= a5 × r10
= (ar2)5
= 25
= 32
Solution 4
x, 2x + 2, 3x + 3, G are four consecutive terms of a G.P.
Then,
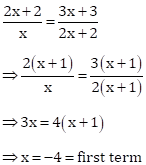
And, 2x + 2 = 2(–4) + 2 = –6
![]()
Now, ![]()
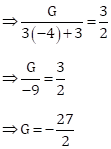
Solution 3
Let the first term = a and the common ratio = r
nth term = arn-1
3rd term – 1st term = 9
ar2 – a = 9
a(r2 – 1) = 9
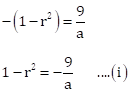
And, 2nd term – 4th term = 18
ar – ar3 = 18
ar(1 – r2) = 18

Substituting in (i),

Then, the G.P. is 3, 3(–2), 3(–2)2, 3(–2)3, …..
That is, 3, –6, 12, –24, …..
Solution 2
Let the first term = a and the common ratio = r
nth term = arn-1
5th term = 32
⇒ ar4 = 32
And, 8th term = 256
⇒ ar7 = 256

And, ar4 = 32
a(2)4 = 32
a × 16 = 32
a = 2
Hence, the first term and the common ratio are 2 and 2, respectively.
Solution 1(f)
Correct option: (b) 185
Let the first term = a and the common ratio = r
3rd term = ar2 = 18
Product of first five terms
= ar0 × ar1 × ar2 × ar3 × ar4
= a5 × r10
= (ar2)5
= 185
Solution 1(e)
Correct option: (b) 3
Let the first term = a and the common ratio = r
nth term = arn-1
4th term = 27
⇒ ar3 = 27
And, 6th term = 243
⇒ ar5 = 1458
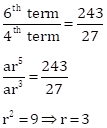
Solution 1(d)
Correct option: (b) 3
Let the three terms in G.P. be a, ![]() and ar, respectively.
and ar, respectively.
![]()
⇒ a3 = 27
⇒ a = 3
Solution 1(c)
Correct option: (a) ![]()
6th term = ar5 = 48
Common ratio, r = 2
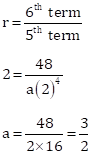
Solution 1(b)
Correct option: (a) 16
x + 9, 10 and 4 are in G.P.
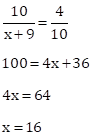
Solution 1(a)
Correct option: (d) either 1 or –1
When k = 1,
![]()
Here, common ratio = –1
When k = –1,
![]()
Here, common ratio = 1
Since k cannot take both the values, k can be either 1 or –1.
Geometric Progression Exercise Ex. 11(A)
Solution 8
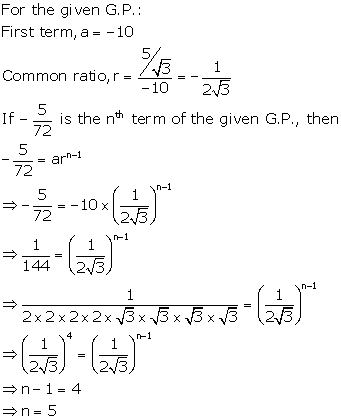
Solution 18

Solution 9

Solution 19

Solution 10
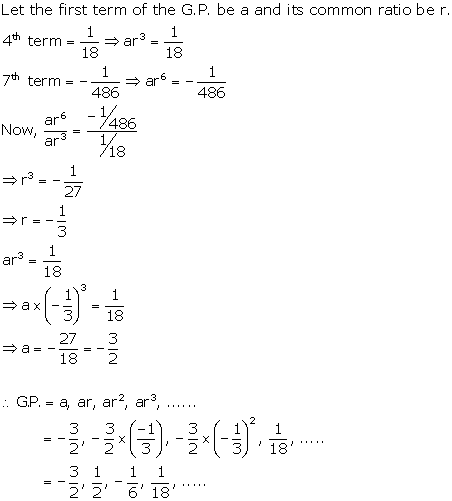
Solution 20
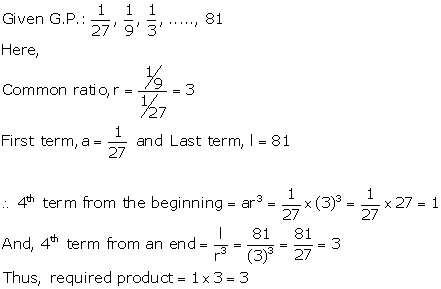
Solution 2

Solution 11

Solution 3

Solution 12

Solution 4

Solution 13

Solution 14

Solution 21(i)
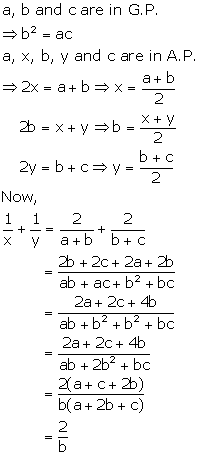
Solution 15

Solution 21(ii)
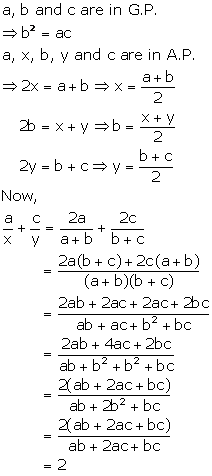
Solution 5

Solution 16

Solution 22
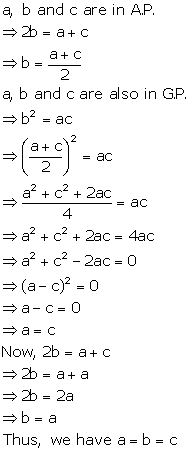
Solution 17

Solution 6

Solution 7
Given series: 2, - 6, 18, - 54 ……
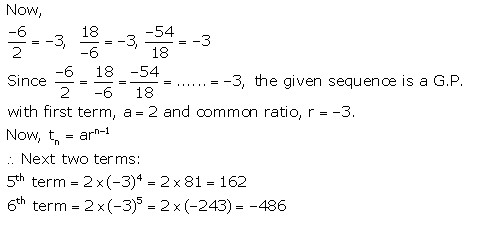
Solution 1(e)
Correct option: (d) ![]()
Let the first term = a and the common ratio, r = 2 ![]() 8th term = 192
8th term = 192
ar7 = 192
a(2)7 = 192
a(128) = 192
![]()
Solution 1(d)
Correct option: (c) 35
Let the first term = a and the common ratio = r
3rd term = ar2 = 3
Product of first five terms
= ar0 × ar1 × ar2 × ar3 × ar4
= a5 × r10
= (ar2)5
= 35
Solution 1(c)
Correct option: (c) ![]()
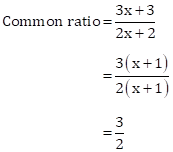
Solution 1(b)
Correct option: (a) 2
Let the first term = a and the common ratio = r
nth term = arn-1
4th term = 16
⇒ ar3 = 16
And, 7th term = 128
⇒ ar6= 128
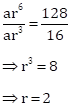
Solution 1(a)
Correct option: (c) 32
First term, a = 8
Common ratio, r = –2
nth term = arn-1
Then, 3rd term = 8(–2)2 = 32
Geometric Progression Exercise Ex. 11(B)
Solution 2(i)

Solution 2(ii)

Solution 2(iii)
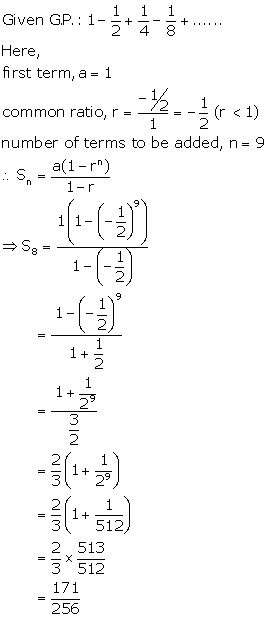
Solution 2(iv)

Solution 2(v)

Solution 2(vi)

Solution 3

Solution 4

Solution 5
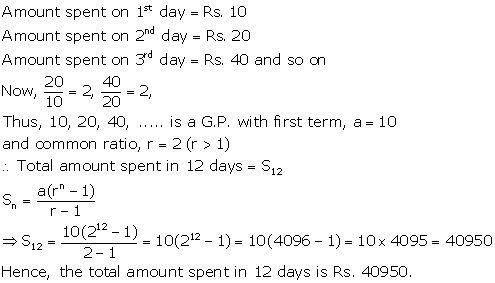
Solution 6

Solution 7
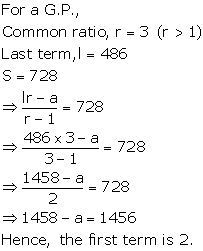
Solution 8

Solution 9

Solution 10
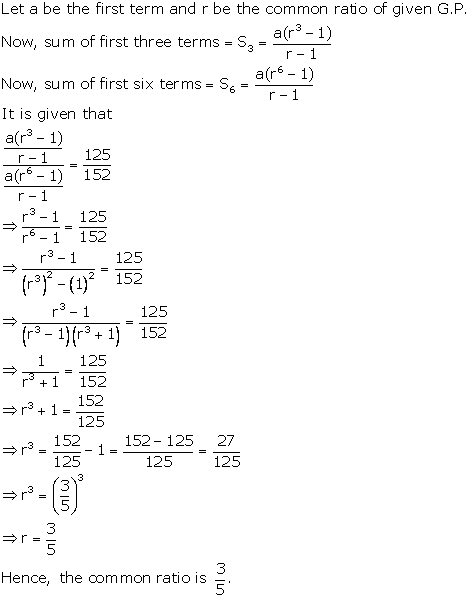
Solution 11
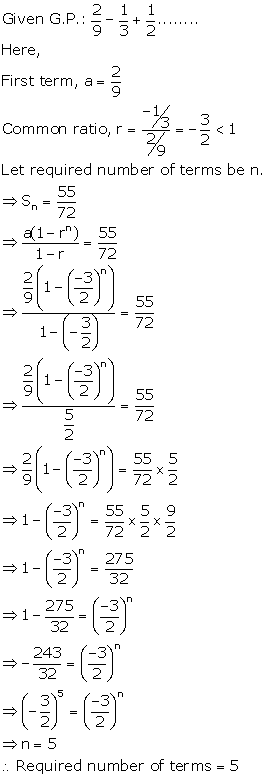
Solution 12
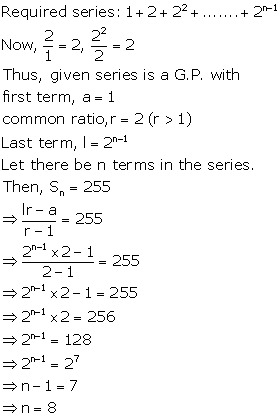
Solution 13(i)
![]()
Solution 13(ii)
![]()
Solution 13(iii)
![]()
Solution 14
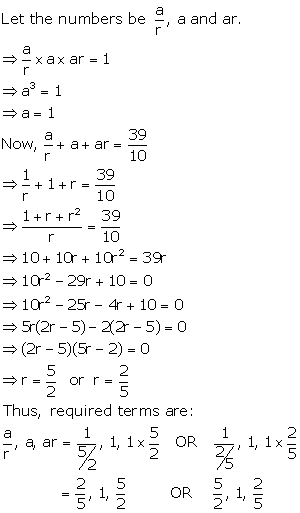
Solution 15

Solution 16
First term (a) = ![]()
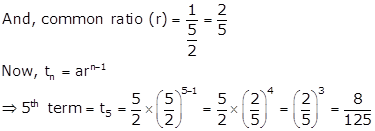
Solution 17
First term (a) = 125
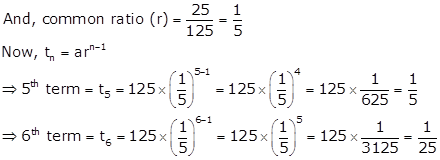
Solution 18
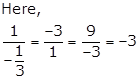
Thus, the given sequence is a G.P. with ![]()
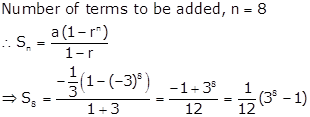
Solution 19
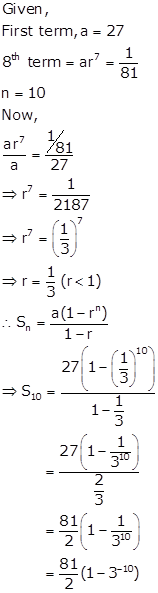
Solution 20
Let the five terms of the given G.P. be
![]()
Given, sum of first two terms = -4
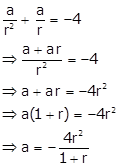
And, 5th term = 4(3rd term)
⇒ ar2 = 4(a)
⇒ r2 = 4
⇒ r = ±2
When r = +2,
![]()
When r = -2,
![]()
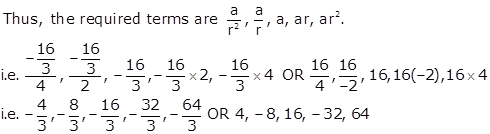
Solution 1(d)
Correct option: (a) ![]()
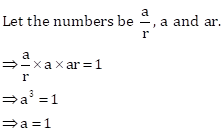


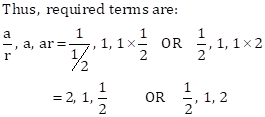
Solution 1(c)
Correct option: (a) 2
Geometric mean between 8 and 32 ![]()
Solution 1(b)
Correct option: (b) 3
Let the first term = a and the common ratio = r
nth term = arn-1
4th term = 54
⇒ ar3 = 54
And, 7th term = 1458
⇒ ar6= 1458
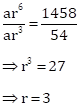
Solution 1(a)
Correct option: (b) 80
a = 2, n = 4 and ![]()
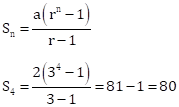
Solution 1(e)
Correct option: (c) 10(220 – 1)
a = 10, n = 20 and ![]()