Class 10 SELINA Solutions Maths Chapter 17 - Circles
Circles Exercise TEST YOURSELF
Solution 1(f)
Correct option: (ii) 80o
∠BOD = 2∠BAD = 2(80o) = 160o
Chord BC = Chord CD
⇒∠BOC = ∠COD
Now, ∠BOC + ∠COD = ∠BOD
⇒ 2∠BOC = ∠BOD = 160o
⇒∠BOC = 80o
Solution 1(e)
Correct option: (ii) 66o
AB is the side of a regular pentagon.
![]()
BC is the side of a regular hexagon.
![]()
∠AOC = ∠AOB + ∠BOC = 72o + 60o = 132o
∠AOC = 2∠APB
132o = 2∠APB
∠APB = 66o
Solution 1(d)
Correct option: (ii) 88o
Arc AB : Arc BC = 11 : 4
⇒∠AOB : ∠BOC = 11 : 4
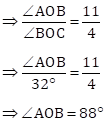
*∠AOC = ∠AOB + ∠BOC = 88o + 32o = 120o, which is not given in options. Hence, according to back answers, if option (ii) is correct, then ∠AOB is to be found.
Solution 1(c)
Correct option: (iii) xo + 2yo = 360o
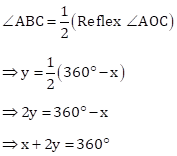
Solution 1(b)
Correct option: (iii) 360o
The sum of the measures of angles of any quadrilateral is 360o.
For a cyclic quadrilateral, each exterior angle equals its opposite interior angles.
Hence, xo + yo + zo + po = 360o
Solution 1(a)
Correct option: (ii) A is true, R is true
Angle in a semi-circle is a right angle.
Hence, the assertion (A) is true.
The measure of ∠ADC is calculated correctly in reason statement.
Hence, the reason statement is true.
Solution 2

Solution 3


Solution 4
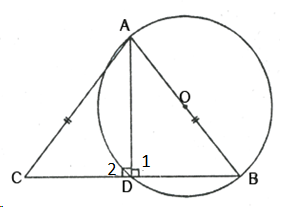
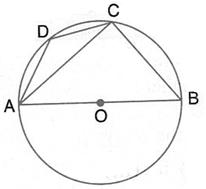
Given - In Δ ABC, AB = AC and a circle with AB as diameter is drawn which intersects the side BC at D.
To prove - D is the midpoint of BC.
Construction - Join AD.
Proof:
∠1 = 90° [Angle in a semi circle]
But ∠1 + ∠2 = 180° [Linear pair]
∴ ∠2 = 90°
Now in right ΔABD and Δ ACD,
Hyp. AB = Hyp. AC [Given]
Side AD = Ad [Common]
∴ By the Right angle - Hypotenuse - Side criterion of congruence, we have
Δ ABD ≅ ΔACD [RHS criterion of congruence]
The corresponding parts of the congruent triangles are congruent.
∴ BD = DC [c.p.c.t]
Hence D is the mid point of BC.
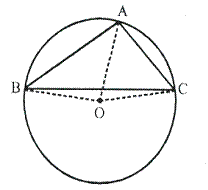
Solution 5
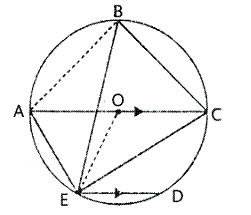
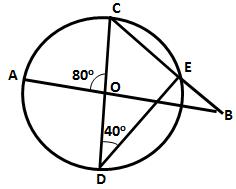
Join OE.
Arc EC subtends ∠EOC at the centre and ∠EBC at the remaining part of the circle.
∠EOC = 2 ∠EBC = 2 × 65° = 130°.
Now in Δ OEC, OE = OC [Radii of the same circle]
∴ ∠OEC = ∠OCE
But, in Δ EOC,
∠OEC + ∠OCE + ∠EOC = 180° [Angles of a triangle]
⇒ ∠OCE + ∠OCE + ∠EOC = 180°
⇒ 2 ∠OCE + 130° = 180°
⇒ 2 ∠OCE = 180° - 130°
⇒ 2 ∠OCE + 50°
⇒ ∠OCE = 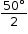 = 25°
= 25°
∴ AC || ED [given]
∴ ∠DEC = ∠OCE [Alternate angles]
⇒ ∠DEC = 25°
Solution 6

Solution 7

Solution 8

Solution 9

Solution 10


Solution 11
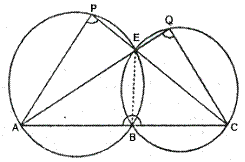

Solution 12
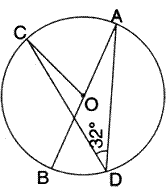

Solution 13
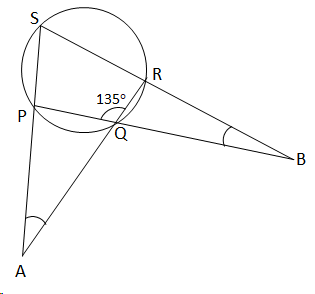

Solution 14
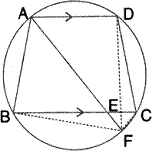

Solution 15
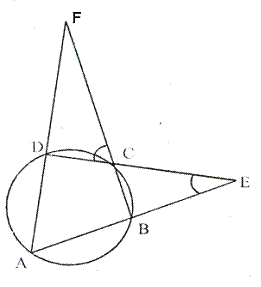

Solution 16
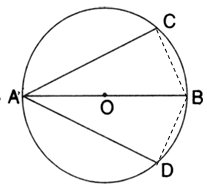

Solution 17
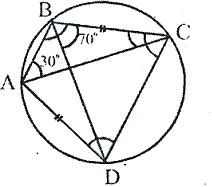

Solution 18


Solution 19
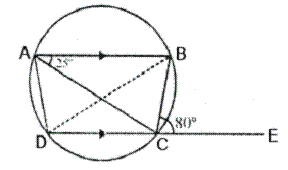

Solution 20
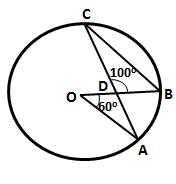
Given - In the figure, CP is the bisector of ∠ABC
To prove - DP is the bisector of ∠ADB
Proof - Since CP is the bisector of ∠ACB
∴ ∠ACP = ∠BCP
But ∠ACP = ∠ADP [Angles in the same segment of the circle]
and ∠BCP = ∠BDP
But ∠ACP = ∠BCP
∴ ∠ADP = ∠BDP
∴ DP is the bisector of ∠ADB
Solution 21

Solution 22
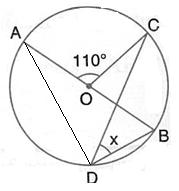
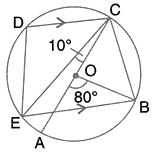
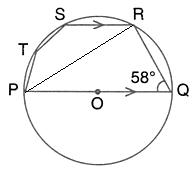
i. AD is parallel to BC, i.e., OD is parallel to BC and BD is transversal.
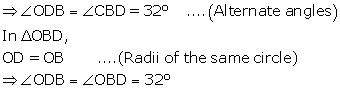


Solution 23
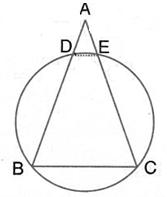
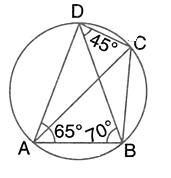
∠DAE and ∠DAB are linear pair
So,
∠DAE + ∠DAB = 180°
∴∠DAB = 110°
Also,
∠BCD + ∠DAB = 180°……Opp. Angles of cyclic quadrilateral BADC
∴∠BCD = 70°
∠BCD = ![]() ∠BOD…angles subtended by an arc on the center and on the circle
∠BOD…angles subtended by an arc on the center and on the circle
∴∠BOD = 140°
In ΔBOD,
OB = OD……radii of same circle
So,
∠OBD =∠ODB……isosceles triangle theorem
∠OBD + ∠ODB + ∠BOD = 180°……sum of angles of triangle
2∠OBD = 40°
∠OBD = 20°
Circles Exercise Ex. 17(A)
Solution 2

Solution 3
Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10
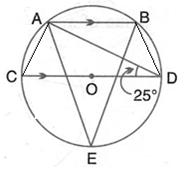

Solution 11
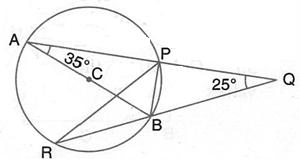

Solution 12
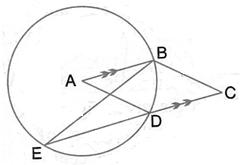

Solution 13
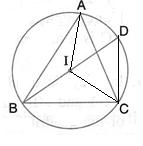

Solution 14
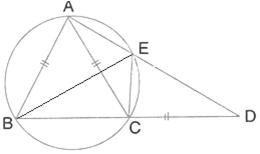
Solution 15

Solution 16

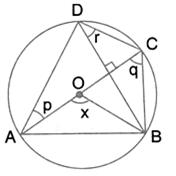
Solution 17

Solution 18

Solution 19

Solution 1(d)
Correct option: (iv) C, B and D are collinear
∠ABD = 90o (angle in a semi-circle)
∠ABC = 90o (angle in a semi-circle)
Now, ∠ABD + ∠ABC = 180o
Therefore, C, B and D are collinear.
Solution 1(c)
Correct option: (ii) 50o
∠APB = ∠ACB = 50o (angles in the same segment)
Chord AB = Chord PB
⇒∠PAB = ∠APB = 50o
Note: Back answer is incorrect
Solution 1(b)
Correct option: (iii) 40o
OA = OB (radii of circle)
⇒ ∠OAB = ∠OBA = 50o
⇒ ∠AOB = 180o – ∠OAB – ∠OBA = 180o – 50o – 50o = 80o
The angle at the centre is twice the angle at remaining circumference.
∴ ∠APB = 80o/2 = 40o
Solution 1(e)
Correct option: (i) 122o
AB is parallel to DC and AC is the transversal.
Hence, ∠BAC = ∠ACD = 32o (alternate angles)
∠DAC = 90o (angle in a semi-circle)
Therefore, ∠DAB = ∠DAC + ∠BAC = 90o + 32o = 122o
Solution 1(a)
Correct option: (ii) 35o
AB is the diameter of a circle with centre O.
Then, ∠BCA = 90o (angle in a semi-circle)
In ∆ABC,
∠A + ∠B + ∠C = 180o
∠A + 55o + 90o = 180o
∠A = 35o
Circles Exercise Ex. 17(B)
Solution 2

Solution 3

Solution 4


Solution 5

Solution 6


Solution 7


Solution 8

Solution 9
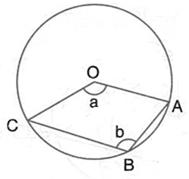
Solution 10
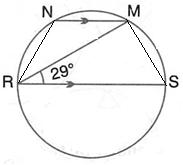

Solution 11
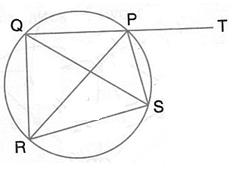

Solution 12
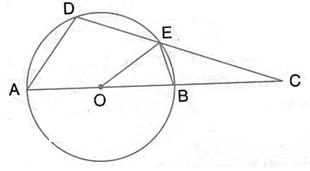

Solution 13
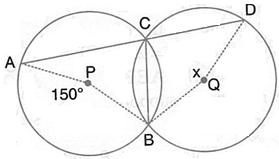

Solution 14


Solution 15
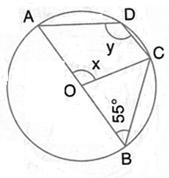

Solution 16
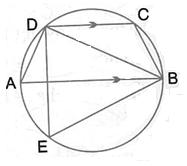
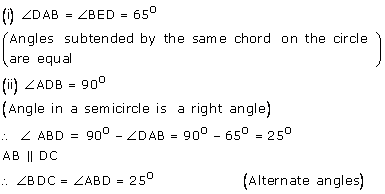
Solution 17
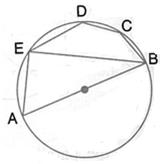
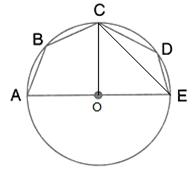
(i) ![]() AEB =
AEB = ![]()
(Angle in a semicircle is a right angle)
Therefore ![]() EBA =
EBA = ![]() -
- ![]() EAB =
EAB = ![]() -
- ![]() =
= ![]()
(ii) AB ![]() ED
ED
Therefore ![]() DEB = EBA =
DEB = EBA = ![]() (Alternate angles)
(Alternate angles)
Therefore BCDE is a cyclic quadrilateral
Therefore ![]() DEB +
DEB + ![]() BCD =
BCD = ![]()
[Pair of opposite angles in a cyclic quadrilateral are supplementary]
Therefore ![]() BCD =
BCD = ![]() -
- ![]() =
= ![]()
Solution 18

Solution 19
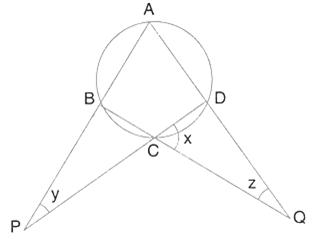
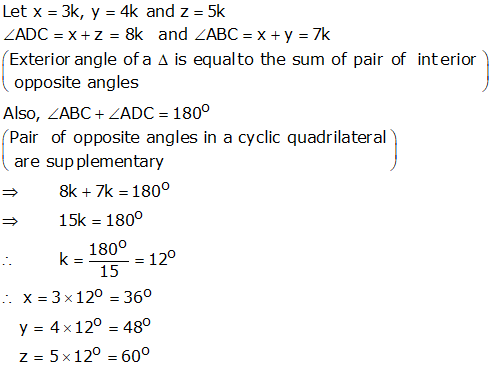
Solution 20

Solution 21

Solution 22

Solution 23

Solution 24

Solution 25


Solution 26

Solution 27

Solution 28

Solution 1(a)
Correct option: (i) 85o
∠DCE = ∠BAD (Exterior angle property of a cyclic quadrilateral)
⇒∠BAD = 95o
AD is parallel to BC and AB is the transversal.
⇒∠BAD + ∠ABC = 180o
⇒∠ABC= 180o – 95o = 85o
Solution 1(b)
Correct option: (iv) 120o
ABC is an equilateral triangle.
⇒∠ABC = 60o
ABCD is a cyclic quadrilateral.
⇒∠ABC + ∠ADC = 180o
⇒∠ADC = 180o – 60o = 120o
Solution 1(c)
Correct option: (iv) 140oJoin OB.
OA = OB (radii of the circle)
⇒∠OBA = ∠OAB = 30o
OC = OB (radii of the circle)
⇒∠OBC = ∠OCB = 40o
∠ABC = ∠OBA + ∠OBC = 30o + 40o = 70o
Therefore, ∠AOC = 2 ×∠ABC = 2 × 70o = 140o
Solution 1(d)
Correct option: (iv) AC//BD
ACQP is a cyclic quadrilateral.
∠ACQ + ∠APQ = 180o …..(i)
BDQP is a cyclic quadrilateral.
∠BDQ + ∠BPQ = 180o ….(ii)
Adding (i) and (ii),
∠ACQ + ∠APQ + ∠BDQ + ∠BPQ = 180o + 180o
∠ACQ + ∠BDQ + (∠APQ + ∠BPQ) = 360o
∠ACQ + ∠BDQ + 180o = 360o (APB is a straight line)
∠ACQ + ∠BDQ = 180o
Since, the interior angles ACQ and BDQ on the same side of the transversal CD are supplementary, AC is parallel to BD.
Solution 1(e)
Correct option: (i) 105o
ABCD is a cyclic quadrilateral.
∠DAC + ∠BCD = 180o (Opposite angles of a cyclic quadrilateral are supplementary)
∠BCD = 180o – 1050 = 75o
AB is parallel to DC and BC is the transversal.
⇒∠ABC + ∠BCD = 180o
⇒∠ABC = 180o – 75o = 105o
Circles Exercise Ex. 17(C)
Solution 2


Solution 3


Solution 4

Solution 5
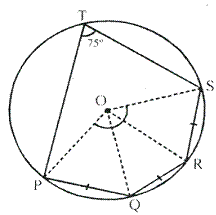

Solution 6

Solution 7
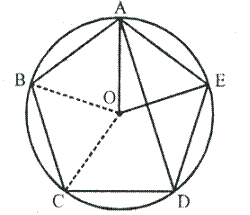

Solution 8
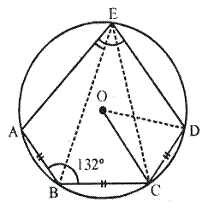

Solution 9
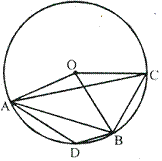

Solution 10

Solution 11
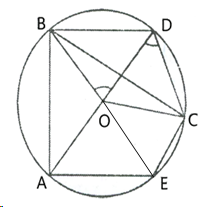
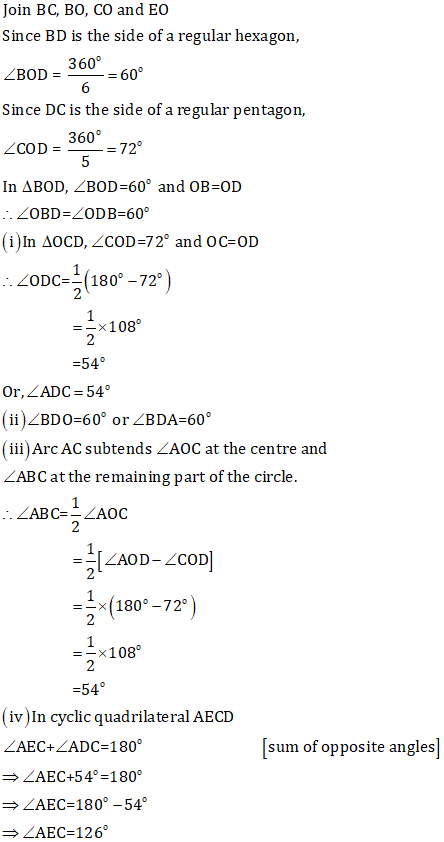
Solution 1(a)
Correct option: (iv) 100o
Chord AB : Chord CD = 3 : 5
⇒∠AOB : ∠COD = 3 : 5
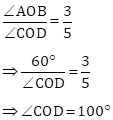
Solution 1(b)
Correct option: (ii) 35o
OA = OB (radii of the circle)
⇒∠OAB = ∠OBA = 55o
In triangle AOB,
∠AOB = 180o – ∠OAB –∠OBA = 180o – 55o – 55o = 70o
Also, ∠AOB = 2∠ACB
70o = 2∠ACB
∠ACB = 35o
Solution 1(c)
Correct option: (ii) 105o
AB is the side of a square.
![]()
BC is the side of a regular hexagon.
![]()
Arc AD = Arc CD
⇒∠AOD = ∠DOC = x
Then, ∠AOB + ∠BOC + ∠AOD + ∠DOC = 360o
90o + 60o + x + x = 360o
2x = 210
x = 105o
Solution 1(d)
Correct option: (i) 36o
AB is the side of a regular pentagon.
![]()
∠AOB = 2∠ACB
72o = 2∠ACB
∠ACB = 36o
Solution 1(e)
Correct option: (iv) 120o
Chord AB = Chord CD = Chord EF
⇒∠AOB = ∠COD = ∠EOF = x
Chord BC = Chord DE = Chord FA
⇒∠BOC = ∠DOE = ∠AOF = y
Now,
∠AOB + ∠COD + ∠EOF + ∠BOC + ∠DOE + ∠AOF = 360o
x + x + x + y + y + y = 360o
3x + 3y = 360o
x + y = 120o
∠AOC = ∠AOB + ∠BOC = x + y = 120o

