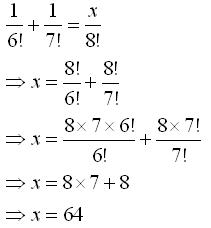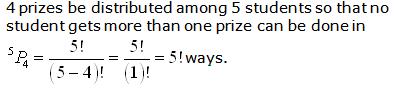Class 11-science RD SHARMA Solutions Maths Chapter 16 - Permutations
Permutations Exercise Ex. 16.1
Solution 1

Solution 2
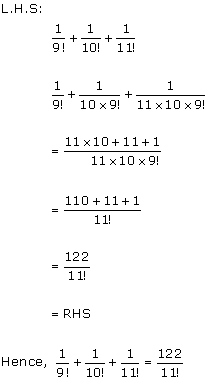
Solution 3(i)
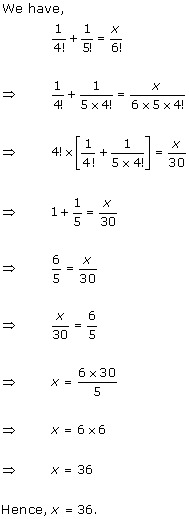
Solution 3(ii)
Solution 3(iii)
Solution 4(i)

Solution 4(ii)

Solution 4(iii)

Solution 4(iv)

Solution 5

Solution 6
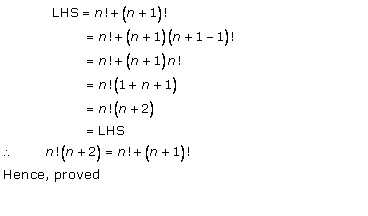
Solution 7
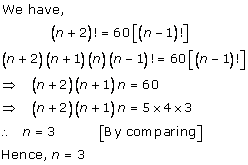
Solution 8

Solution 9

Solution 10

Solution 11(i)
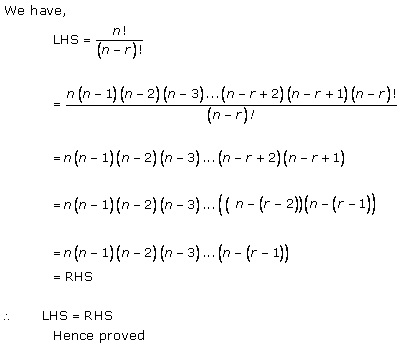
Solution 11(ii)

Solution 12

Permutations Exercise Ex. 16.2
Solution 1

Solution 2

Solution 3

Solution 4

Solution 4

Solution 5

Solution 6
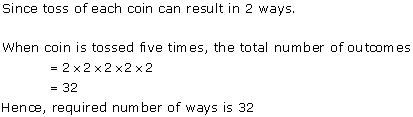
Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12
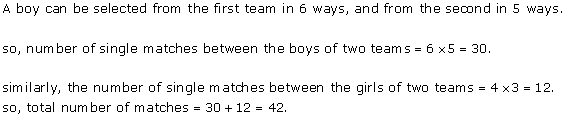
Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18
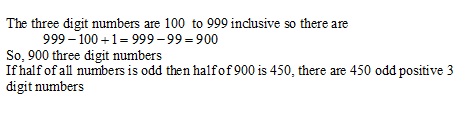
Solution 19(i)

Solution 19(ii)

Solution 20

Solution 21

Solution 22

Solution 23

Solution 24
One-digit odd number:
3 possible ways are there. These numbers are 3 or 5 or 7.
Two-digit odd number:
Tens place can be filled up by 3 ways (using any of the digit among 3, 5 and 7) and then the ones place can be filled in any of the remaining 2 digits.
So, there are 3
Three-digit odd number:
Ignore the presence of zero at ones place for some instance.
Hundreds place can be filled up in 3 ways (using any of any of the digit among 3, 5 and 7), then tens place in 3 ways by using remaining 3 digits (after using a digit, there will be three digits) and then the ones place in 2 ways.
So, there are a total of 3
To obtain the even 3-digit numbers, ones place can be filled up in 1 way (only 0 to be filled), hundreds place in 3 ways (using any of the digit among 3, 5, 7) and then tens place in 2 ways (using remaining 2 digits after filling up hundreds place).
So, there are a total of 1
So, number of three-digit odd numbers using the digits 0, 3, 5 and 7 (repetition not allowed) = 18 - 6 = 12.
Therefore, odd numbers less than 1000 can be formed by using the digits 0, 3, 5, 7 when repetition of digits is not allowed are 3 + 6 + 12 = 21.
Solution 25

Solution 26

Solution 27

Solution 28

Solution 29
Solution 30

Solution 31

Solution 32

Solution 33
The given digits are 1, 2, 3 and 4. These digits can be repeated while forming the numbers. So, number of required four digit natural numbers can be found as follows.
Consider four digit natural numbers whose digit at thousandths place is 1.
Here, hundredths place can be filled in 4 ways. (Using the digits 1 or 2 or 3 or 4)
Similarly, tens place can be filled in 4 ways. (Using the digits 1 or 2 or 3 or 4)
Ones place can be filled in 4 ways. (Using the digits 1 or 2 or 3 or 4)
Number of four digit natural numbers whose digit at thousandths place is 1 = 4 ![]() 4
4 ![]() 4 = 64
4 = 64
Similarly, number of four digit natural numbers whose digit at thousandths place is 2 = 4 ![]() 4
4 ![]() 4 = 64
4 = 64
Now, consider four digit natural numbers whose digit at thousandths place is 4:
Here, if the digit at hundredths place is 1, then tens place can be filled in 4 ways and ones place can also be filled in 4 ways.
If the digit at hundredths place is 2, then tens place can be filled in 4 ways and ones place can also be filled in 4 ways.
If the digit at hundredths place is 3 and the digit at tens place is 1, then ones place can be filled in 4 ways.
If the digit at hundredths place is 3 and the digit at tens place is 2, then ones place can be filled only in 1 way so that the number formed is not exceeding 4321.
Number of four digit natural numbers not exceeding 4321 and digit at thousandths place is 3 = 4 ![]() 4 + 4
4 + 4 ![]() 4 + 4 + 1 = 37
4 + 4 + 1 = 37
Thus, required number of four digit natural numbers not exceeding 4321 is 64 + 64 + 64 + 37 = 229.
Solution 34

Solution 35
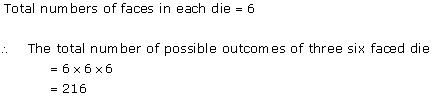
Solution 36

Solution 37

Solution 38

Solution 39

Solution 40

Solution 41

Solution 42
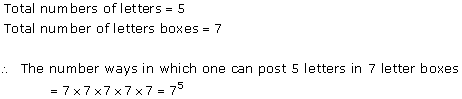
Solution 43

Solution 44

Solution 45

Solution 46

Solution 47(i)
Solution 47(ii)
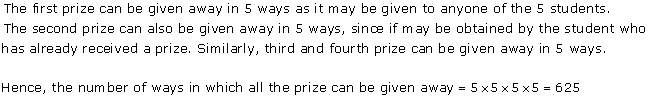
Solution 47(iii)

Solution 48
Each lamps has two possibilities either it can be switched on or off.
There are 10 lamps in the hall.
So the total numbers of possibilities are 210.
To illuminate the hall we require at least one lamp is to be switched on.
There is one possibility when all the lamps are switched off. If all the bulbs are switched off then hall will not be illuminated.
So the number of ways in which the hall can be illuminated is 210-1.
Permutations Exercise Ex. 16.3
Solution 1(ii)

Solution 1(iii)

Solution 1(iv)

Solution 1(i)

Solution 2

Solution 3
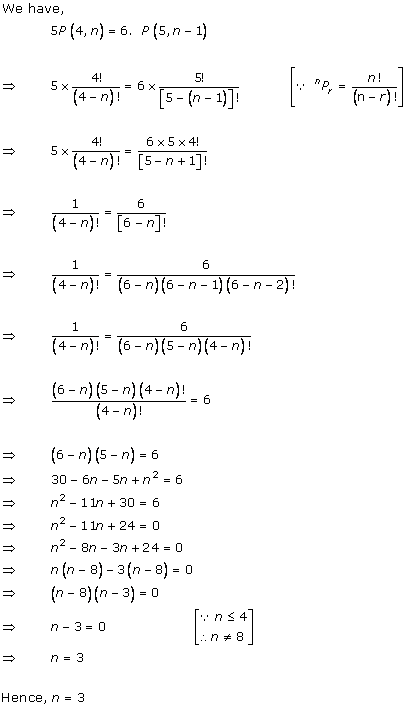
Solution 4

Solution 5
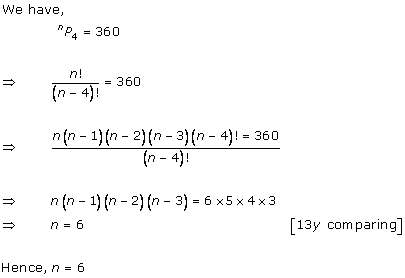
Solution 6

Solution 7

Solution 8
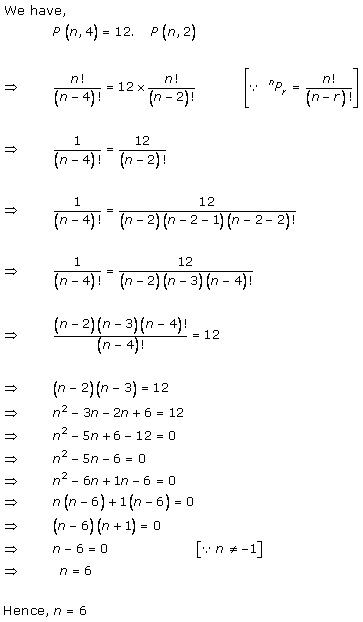
Solution 9

Solution 10
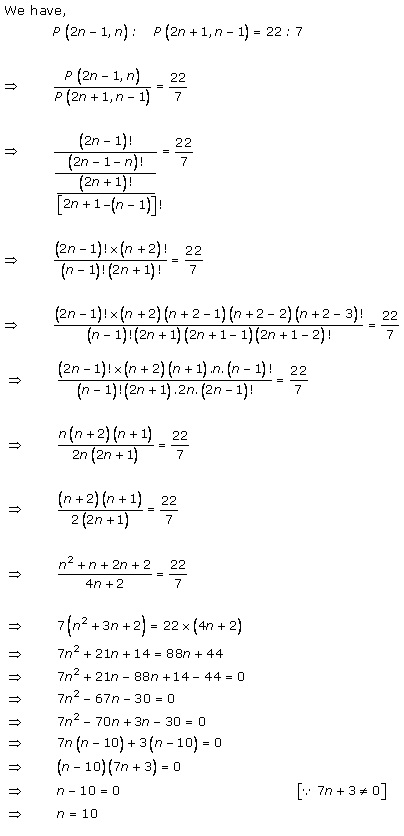
Solution 11

Solution 12
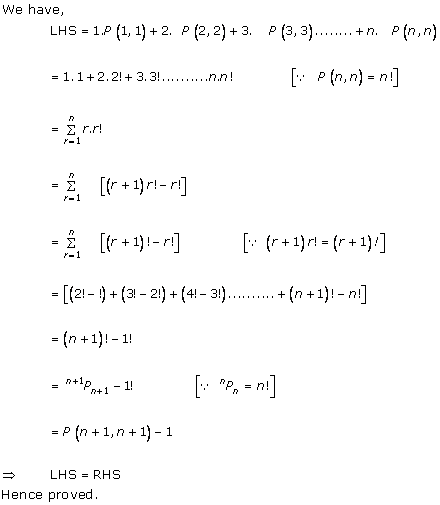
Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18
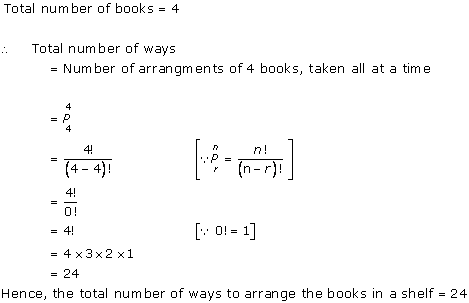
Solution 19

Solution 20

Solution 21

Solution 22

Solution 23

Solution 24

Solution 25

Solution 26

Solution 27

Solution 28
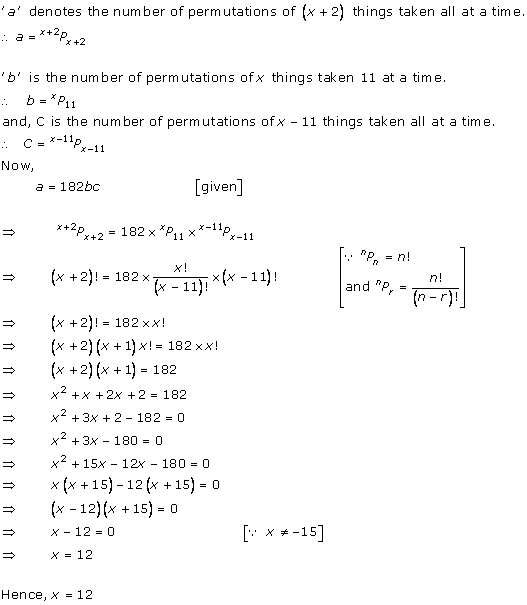
Solution 29

Solution 30

Solution 31

Solution 32
Permutations Exercise Ex. 16.4
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6
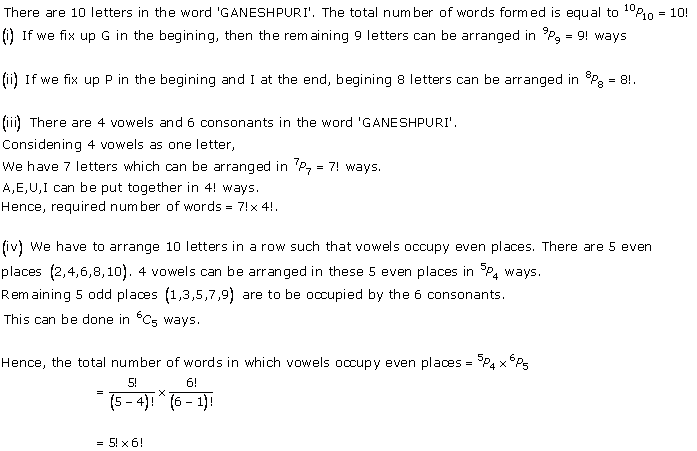
Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12

Permutations Exercise Ex. 16.5
Solution 1(i)

Solution 1(ii)

Solution 1(iii)

Solution 1(iv)
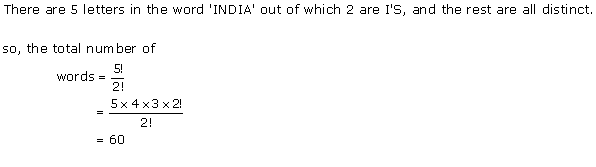
Solution 1(v)

Solution 1(vi)
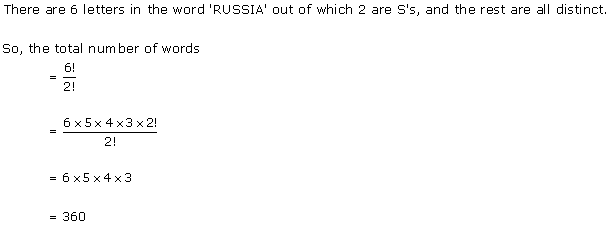
Solution 1(vii)

Solution 1(viii)
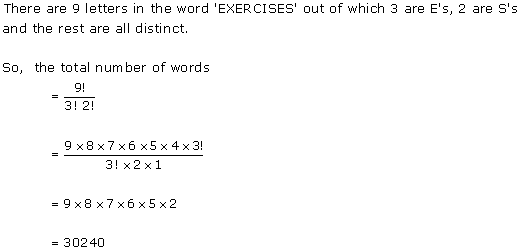
Solution 1(ix)

Solution 2

Solution 3

Solution 4
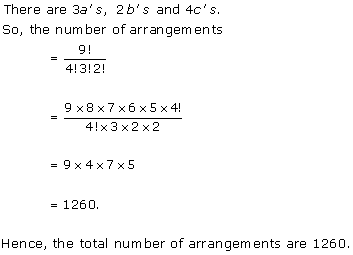
Solution 5

Solution 6

Solution 7

Solution 8
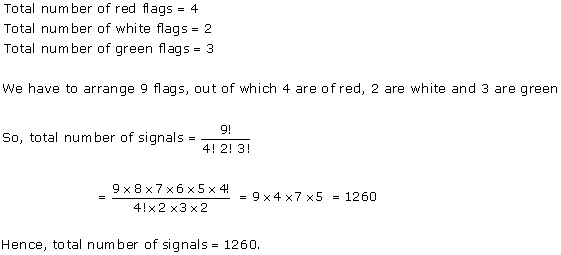
Solution 9

Solution 10

Solution 11
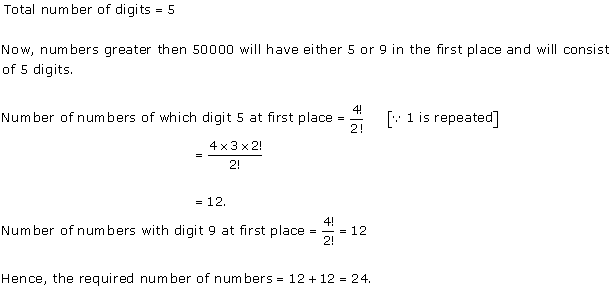
Solution 12

Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18
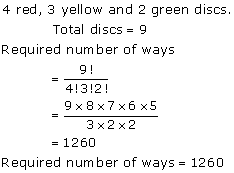
Solution 19

Solution 20

Solution 21

Solution 22

Solution 23

Solution 24

Solution 25

Solution 26

Solution 27

Solution 28

Permutations Exercise Ex. 16VSAQ
Solution 1
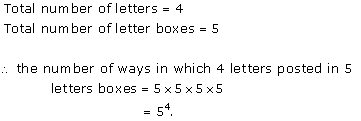
Solution 2
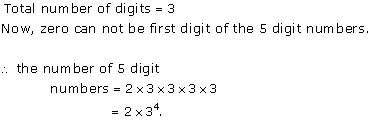
Solution 3
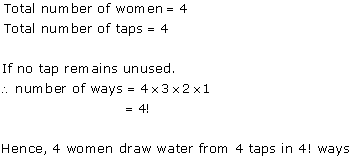
Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11
First we will find the least factorial term divisible by 14.
As 7!=7x6x5! is divisible by 14 leaving remainder zero.
Hence terms 7! onwards can be written as multiple of 7!.
8!=8x7!, 9!=9x8x7!... like ways 200! can also be written as multiple of 7!.
So all the terms 7! onwards are divisible by 14 leaving remainder zero.
1! + 2! + 3! + 4! + 5! + 6!
=1+2+6+24+120+720
=873
Hence remainder obtained when 1! + 2! + 3! + ….+ 200! is divided by 14 is 5.
Solution 12

Solution 13