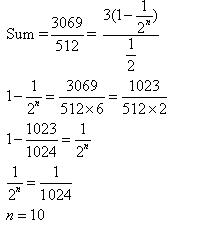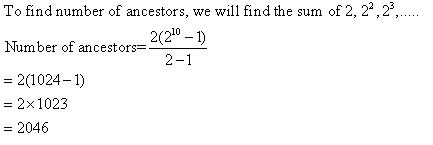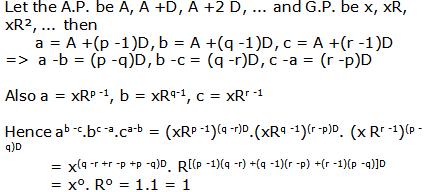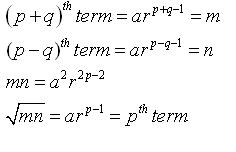Class 11-science RD SHARMA Solutions Maths Chapter 20 - Geometric Progressions
Ex. 20.1
Ex. 20.2
Ex. 20.3
Ex. 20.4
Ex. 20.5
Ex. 20.6
Ex. 20VSAQ
Geometric Progressions Exercise Ex. 20.1
Solution 1
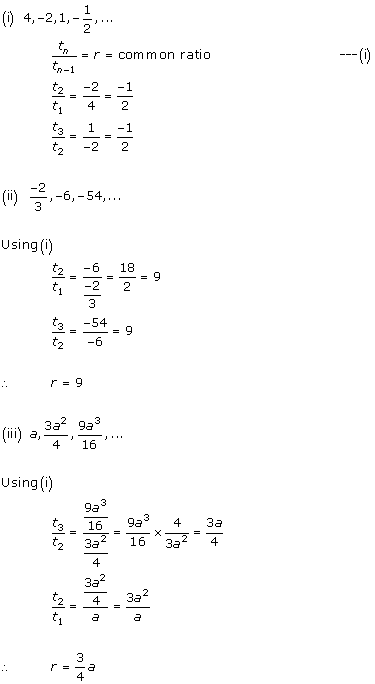
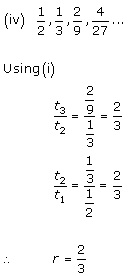
Solution 2

Solution 3
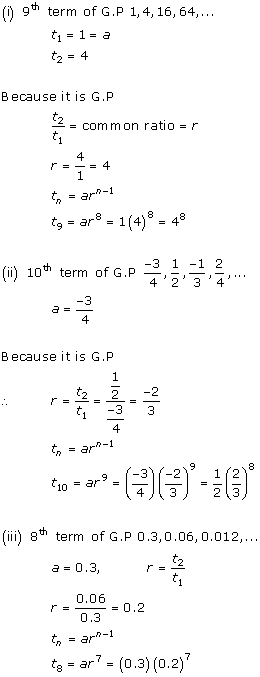

Solution 4
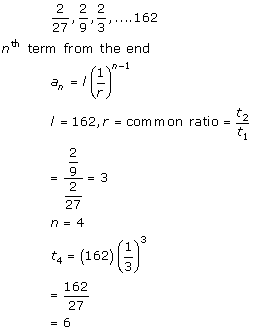
Solution 5

Solution 6(i)

Solution 6(ii)

Solution 6(iii)

Solution 6(iv)

Solution 7
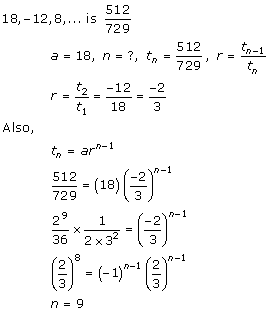
Solution 8

Solution 9
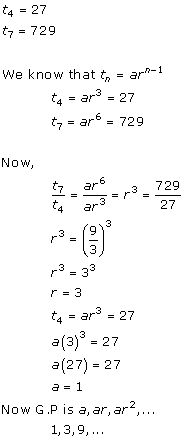
Solution 10

Solution 11

Solution 12

Solution 13
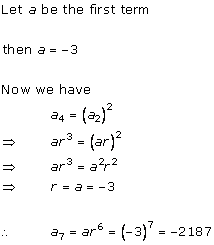
Solution 14
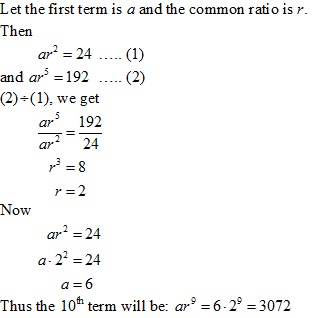
Solution 15

Solution 16

Solution 17
Geometric Progressions Exercise Ex. 20.2
Solution 1

Solution 2

Solution 3
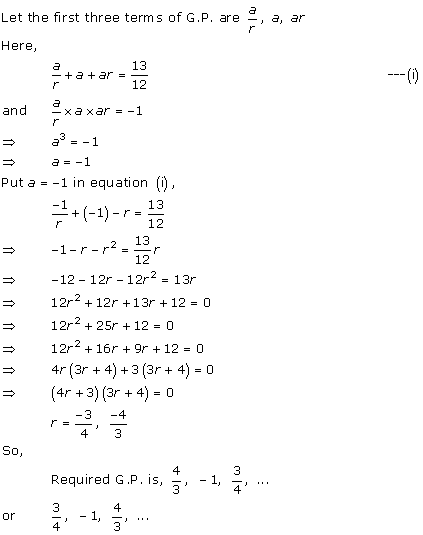
Solution 4

Solution 7

Solution 8

Solution 9

Solution 5
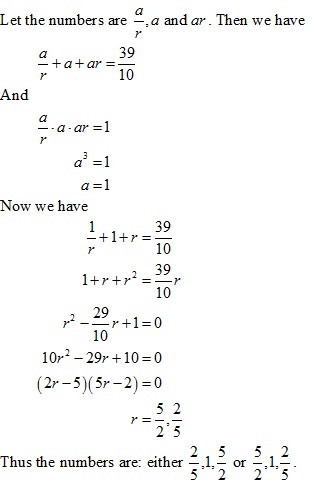
Solution 6
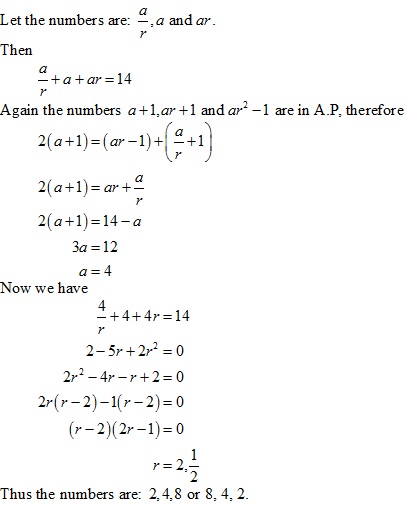
Geometric Progressions Exercise Ex. 20.3
Solution 1(i)

Solution 1(ii)

Solution 1(iii)

Solution 1(iv)

Solution 1(v)

Solution 2(i)
Solution 2(ii)
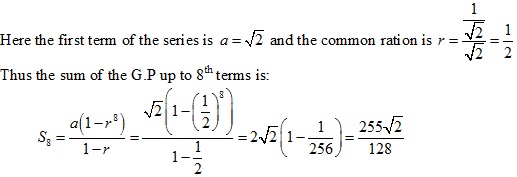
Solution 2(iii)

Solution 2(iv)
Solution 2(v)

Solution 2(vi)

Solution 2(vii)
Solution 2(viii)
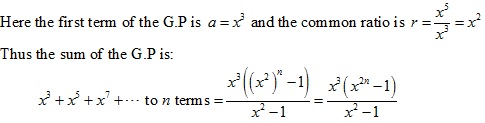
Solution 2(ix)

Solution 3(i)

Solution 3(ii)

Solution 3(iii)

Solution 4(i)

Solution 4(ii)
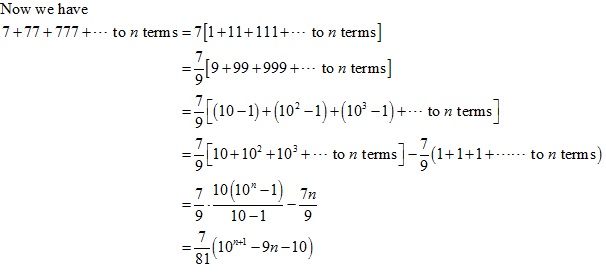
Solution 4(iii)

Solution 4(iv)
Solution 4(v)
Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10
Solution 11

Solution 12
Solution 13
Solution 14
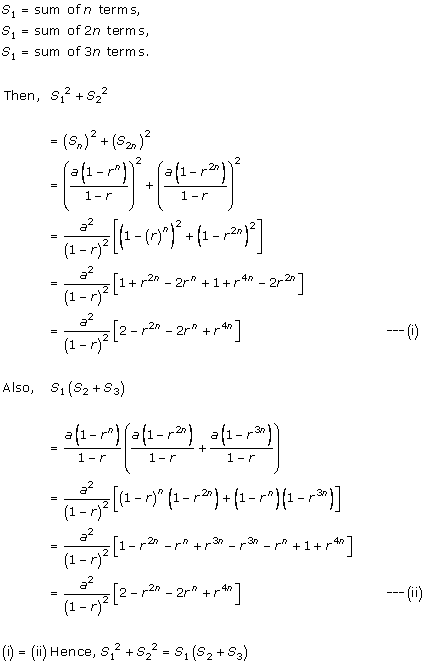
Solution 15

Solution 16
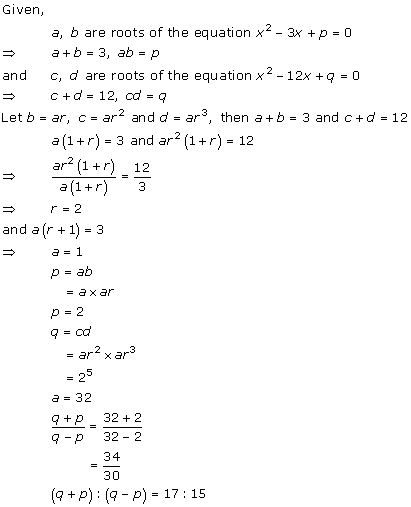
Solution 17
Solution 18
Solution 19
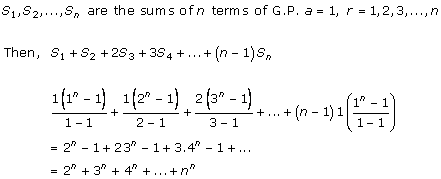
Solution 20

Solution 21

Solution 22

Geometric Progressions Exercise Ex. 20.4
Solution 1(i)
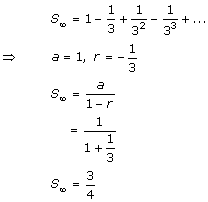
Solution 1(ii)

Solution 1(iii)
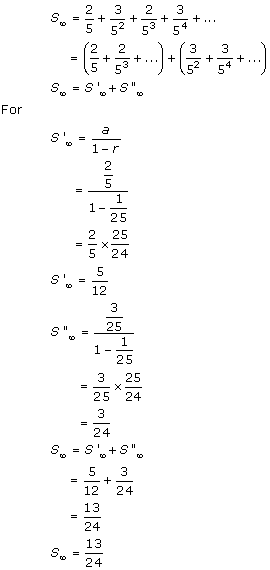
Solution 2

Solution 3

Solution 4

Solution 5

Solution 6
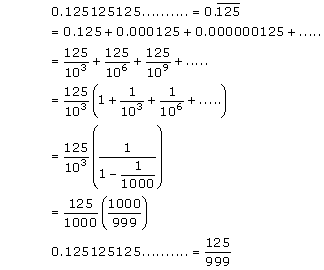
Solution 7
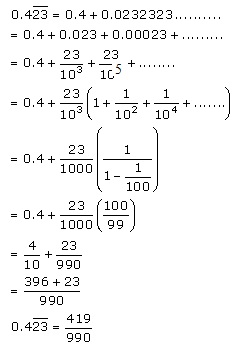
Solution 8(i)
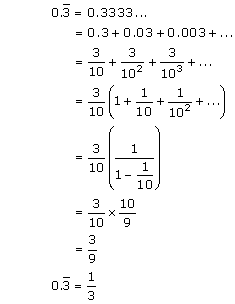
Solution 8(ii)

Solution 8(iii)

Solution 9

Solution 10

Solution 11

Solution 12

Solution 13

Solution 1(iv)
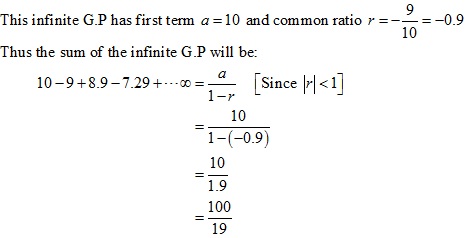
Solution 1(v)
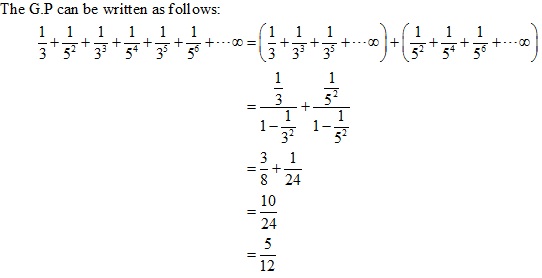
Solution 8(iv)

Geometric Progressions Exercise Ex. 20.5
Solution 1

Solution 2
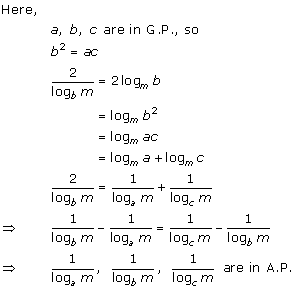
Solution 3
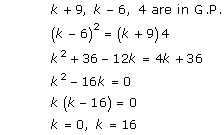
Solution 4
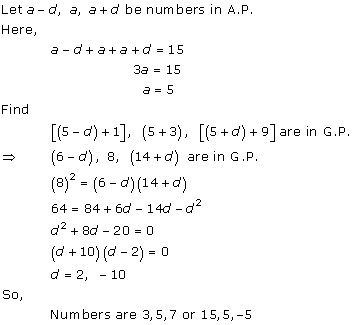
Solution 5

Solution 6
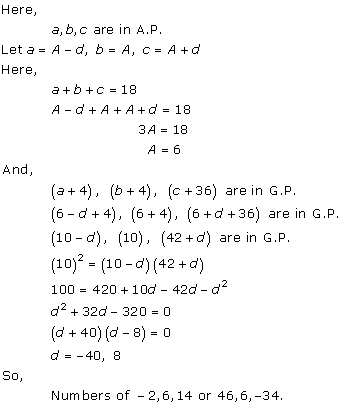
Solution 7

Solution 8(I)
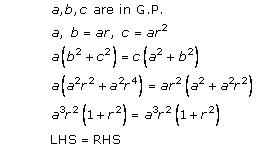
Solution 8(ii)
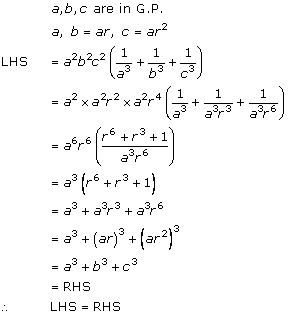
Solution 8(iii)

Solution 8(iv)
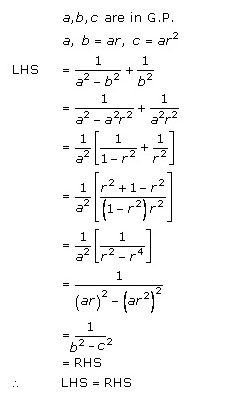
Solution 8(v)

Solution 9(i)

Solution 9(ii)

Solution 9(iii)
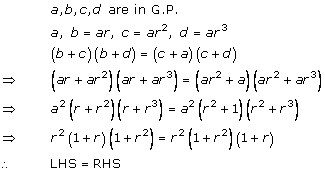
Solution 10(i)
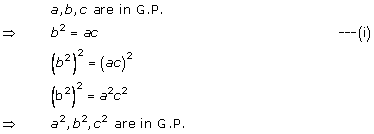
Solution 10(ii)

Solution 10(iii)

Solution 11(i)

Solution 11(ii)

Solution 11(iii)

Solution 11(iv)

Solution 12

Solution 13

Solution 14
Solution 15
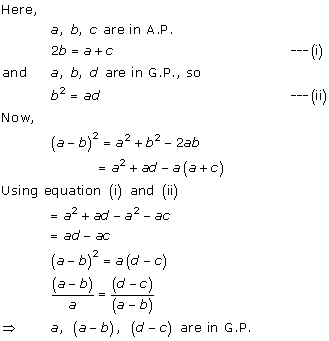
Solution 16

Solution 17

Solution 18
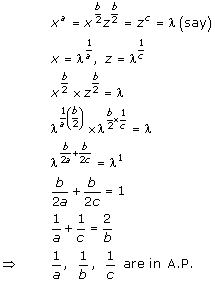
Solution 19

Solution 20

Solution 21

Solution 22

Solution 23
Geometric Progressions Exercise Ex. 20.6
Solution 1
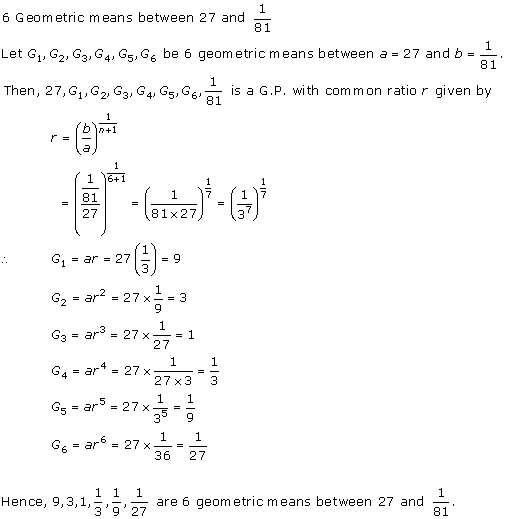
Solution 2
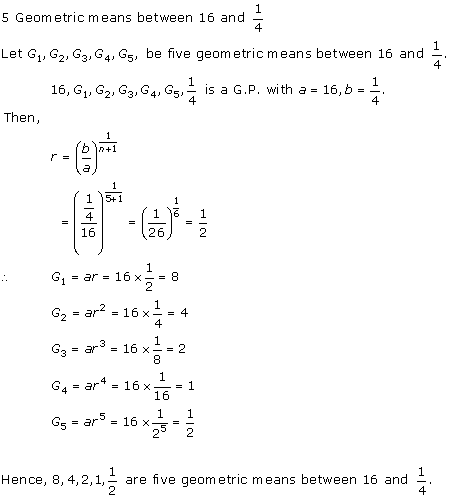
Solution 3

Solution 4
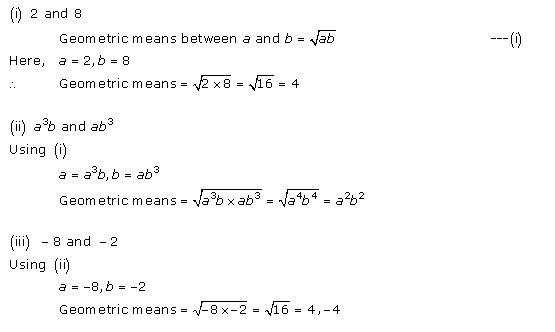
Solution 5
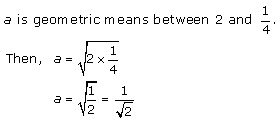
Solution 6
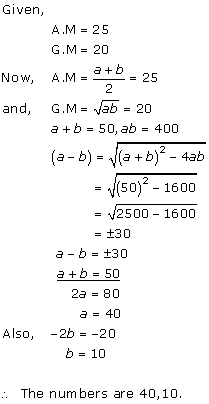
Solution 7
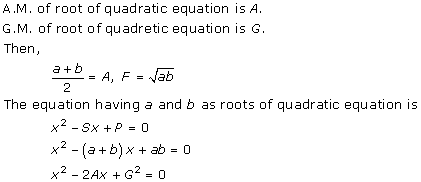
Solution 8

Solution 9

Solution 12

Solution 13
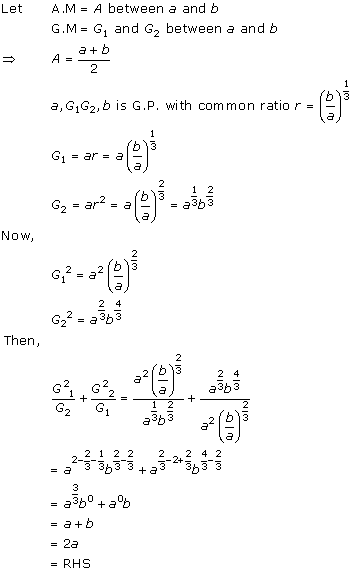
Solution 10
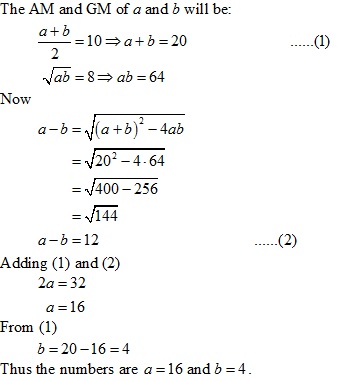
Solution 11

Geometric Progressions Exercise Ex. 20VSAQ
Solution 2
Solution 1
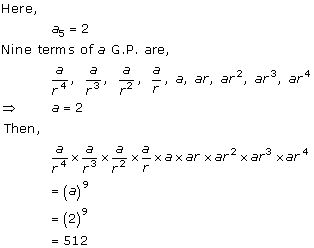
Solution 3

Solution 4

Solution 5
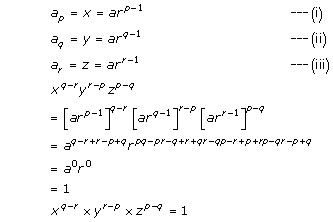
Solution 6

Solution 7
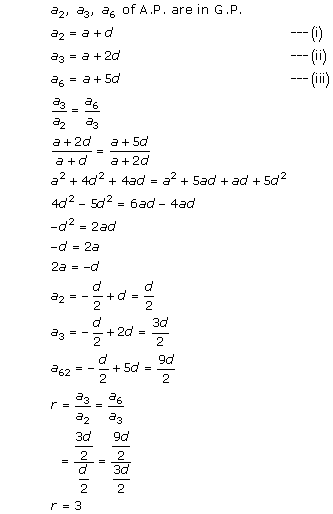
Solution 8

Solution 9

Solution 10