Class 11-science H C VERMA Solutions Physics Chapter 3: Rest and Motion Kinematics

Rest and Motion Kinematics Exercise 51

Solution 1

(a)

Distance travelled = 50+40+20

=110m

(b)

Displacement =50 ĵ +40 î- 20ĵ

=40î+30 ĵ

| disp |=

=50m at an angle of Ɵ=tan^-1() =37° north to east

Solution 2

Distance travelled = 20+40 =60m

Displacement=20m in the negative direction

Solution 3

(a)

_avg/plane = = = 520kmph

(b)

_avg/bus= = = 40kmph

(c)

_avg/plane= = = 520kmh

(d)

_avg/bus= =260/8 = 32.5kmph

Solution 4

(a)

V_avg==

V_avg =32kmph

(b)

_avg=displacement/time

_avg =0

Solution 5

u=0; v=18 = 5m/s; t=2sec

v=u+at

5=0+a(2)

a=2.5m/s²

Solution 6

Acceleration=slope of (v-t) graph

a=tan θ =

=2.5m/s²

Distance=Area under (v-t) graph

=20

=80m

Solution 7

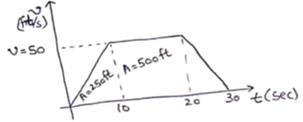
By velocity-time graph,

Acceleration =slope=

V=50m/s

Distance=Area of v-t graph

= (30+10) (50)

=1000ft

Solution 8

(a) Acceleration=slope of v-t graph

== 0.6m/s²

(b) Distance travelled = Area under v-t graph

=(2+8)10

=50m

Solution 9

(a) Velocity=displacement/time

==10m/s

(b) Instantaneous velocity=slope of v-t graph

At t=2.5s; slope== 20m/s

At t= 5s; slope=0m/s

At t=8s; slope== 20m/s

At t=12s; slope== -20m/s

Solution 10

Distance =Area of v-t graph

=() + ()

=100m

Displacement=() + ()

Displacement=0

_avg=

_avg=0

Rest and Motion Kinematics Exercise 52

Solution 11

Average velocity is zero when displacement is zero

At t=0; x=20 and again at t=12; x=20

Solution 12

Direction of instantaneous velocity of point B must be same as direction of average velocity.

So, point is approximately(5,3)

Solution 13

u=4m/s; a=1.2m/s²; t=5sec

Distance travelled

s=ut+at²

s = (4)(5) +(1.2) (5)²

=35m

Solution 14

u=43.2=12m/s; v=0; a=-6m/s²

Using,

v²=u²+2as

O²=(12)²-26s

s=12m

Solution 15

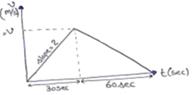
A=slope=

v=60m/s

(a) Distance=Area of v-t graph

=(30+60) (50)

=2700m

=2.7km

(b) Maximum speed

V=60m/s

(c)

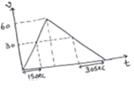
Velocity 30m/s is achieved at t=15sec and t=60sec

Area of (v-t) graph in first 15 second

s= (15)(30) =225m

Area of (v-t) graph in first 60 sec

S= ×30×60+ (60+30)(3)

=2250m

=2.25km

Solution 16

u=16m/s; v=0m/2; s=0.4m

v²=u²+2as

0²=(1)²+2(a)(0.4)

a=-320m/s²

v=u+at

0=16+(-320)t

t=0.05sec

Solution 17

u=350m/s; v=0; s=5×10^-2m

v²=2²+2as

0²=(350)²+2(a)(0.05)

a=-12.25×10⁵m/s²

Solution 18

u=0; t=5sec; v=18×5/18=5m/s

v=u+at

5=0+a(5)

a=1m/s²

S=ut+at²

S=0+ (a)(5)²

S=12.5m

V_avg=distance/time=

V_avg=2.5m/s

Solution 19

Speed of car=54×=15m/s

Distance travelled during reaction time

S₁=vt

=15×0.2=3m

When brakes are applied

u=15m/s; a=-6m/s²;v=0m/s

v²=u²+2as

0²=(15)²+2(-6)S₂

S₂=18.75m

Total distance=S₁+S₂

=3+18.75

=21.75m

≈22m

Solution 20

If initial velocity is u and deacceleration is -a then braking distance

v²= u²+2as

0²=u²- 2aS

S_b= (Braking distance)

S_R=u×t_R (Reaction distance)

Total distance = S_b+S_R

Solve table with given values and above formulas

Solution 21

V_bike=72=20m/s

V_police=90=25m/s

Distance travelled by culprit in 10sec = speed × time

=20×10

=200m

Time to catch culprit by police=Relative distance/Relative speed

T=40sec

So, police travels distance of =25×40

=1000m=1km

Solution 22

₁=60=16.6m/s

₂=42=11.6m/s

Relative velocity =16.6-11.6

V_rel=5m/s

d_res=10m

Time to cross===2sec

In 2 sec, 1^st car moves=16.6×2

=33.2

Length of road=33.2+length of car

=33.2+5

≈38m

Solution 23

u=50m/s; v=0m/s; a=-g

(a) v²=u²+2as

0²=(50)²+2(g)s

s=125m

(b) v=u+at

0=50-gt

t=5sec

v²=u²+2as

=(50)²-2(g)(62.5)

v≈35m/s

Solution 24

u=7m/s; a=-g; s=-60

s=ut+at²

-60=7t-(g)t²

t=4.28sec

Solution 25

(a) u=28m/s; v=0m/s; a=-g

v²=u²+2as

0²=(2s)²+2(-g)(s)

s=40m

(b) Velocity at one second before H_max=Velocity after one second of H_max

So, after H_maxis attained

u=0; a=g; t=1

v=u+at

v=9.8m/s

v=9.8m/s only

Solution 26

For every ball; u=0 and a=g

When 6^th ball is dropped, 5^thball moves for 1 second, 4^th ball moves for 2 seconds, 3^rd ball moves for 3 seconds

Position

S=ut+at²

3^rd ball S₃=0+ (g)(3)²=44.1m

4^th ball S₄=0+ (g)(2)²=19.6m

5^th ball S₅=0+ (g)(1)²=4.9m

Rest and Motion Kinematics Exercise 53

Solution 27

For kid,

u=0; a=g; s=11.8-1.8

s=10m

s=ut+at²

10=0+ (g)t²

t=1.42sec

In this time, man has to reach building

Speed==

=4.9m/s

Solution 28

For berry,

u=0; a=g; s=12.1m

s=ut+at²

12.1=0+ (g)t²

t=1.57sec

Distance moved by cadets=v× t

=(6)(1.57)

=2.6m

The cadet, 2.6m away from tree will receive berry on his uniform

Solution 29

For last 6m,

t=0.2sec; s=6m; a=g

s=ut+at²

6=u(0.2) + (g)(0.2)²

u=29m/s

Before last 6m,

u=0; a=g; v=29m/s

v²=u²+2as

(29)²=0²+2(g)s

S₁=42m

Total distance=42+6=48m

Solution 30

For ball in air

u=0m/s; a=g; s=5m

s=ut+at²

5=0+ (g)t²

v=u+at

v=0+g

For ball in sand

u=; v=0m/s; s=0.1m

v²=u²+2as

0²=()²+2(a)(0.1)

a=-490m/s²

Solution 31

For coin-lift

u_rel=0m/s

t_rel=1sec

s_rel=6ft

s_rel=u_relt+a_relt²

6=a_rel(1)²

a_rel=12 ft/sec²

g-a_lift=12

a_lift=32-12

a_lift=20ft/sec²

Solution 32

x-axis y-axis

u_x=20m/s u_y=0m/s

a_x=0m/s² a_y=gm/s²

(a) s_y=u_yt+a_yt²

100=0+ (9.8)t²

t=4.5sec

(b) s_x=u_xt

=(20)(4.5)

s_x=90m

v_x =20 v_y=0+ (9.8)(4.5)

v_y=44.1m/s

v=49m/s at that is 66° from ground

Solution 33

u=40m/s; θ=60°

(a)

H_max==

H_max=60m

(b)

R==

R=80√3m

Solution 34

y=x tan θ-

=(40×3)tan45-

=120-112.4

y=7.5ft < height of goalpost

So, football will reach the goalpost

Solution 35

x-axis y-axis

s_x=2m u_y=0

a_x=0 a_y=g

s_y=19.6cm

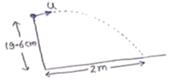
s_y=u_yt+a_yt²

=0+ (9.8)t²

s_x=u_xt+a_xt² t=0.2sec

2=u_xt+a_xt²

2=u_x(0.2)+0

u_x=10m/s

Solution 36

Range to be covered by bike=11.7+5=16.7ft

16.6=

u=32ft/sec

Solution 37

Tan θ=228/171=4/3

θ=53°

x-axis y-axis

u_x=15sin53 u_y=15cos53

u_x=12ft/sec u_y=9ft/sec

a_y=32ft/sec²

s_y=171ft

s_y=u_yt+a_yt²

171=9t+ (32)t²

t=3sec

s_x=12×3

=36ft

Packet will fall short by = 228-36=192ft

Solution 38

R=19.88m

Ball will hit 5m away wall

If wall is at a distance of 22m, it will not hit directly

Solution 39

Let particle reaches from A to B in time t.

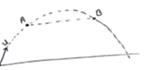
By symmetry, AB line is horizontal

So, displacement AB=u_xt

Velocity==

V_avg=u cos θ

Solution 40

During release, u_plane₌u_bomb

Along x-axis,

u_rel₌0

a_rel=0

So, at any time, s_rel=0

So, bomb will always be below and will explode

If plane is at some angle then also u_plane_/x-axis=u_bomb_/x-axis

i.e. Along x-axis u_rel=0

So, bomb explodes below plane

Solution 41

Time of flight for ball=

t=2sec

For ball-car, along horizontal direction

u_rel=0

a_rel=1

t=2

s_rel=u_relt₊ a_relt²

=0+ (1)(2)²

s_rel=2m

Solution 42

For minimum velocity ball will just be touching point B

If A is origin then coordinates of B(40,-20)

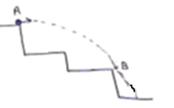
Y=x tan θ - g

-20=40tan0°-

u=200cm/s

u=2m/s

Solution 43

Time taken by ball=Time taken by truck to cover 58.8m

Time= ==4sec

(a)

For Truck, ball will seems to travel in vertical direction

Time to reach H_max by ball==2sec

v=0; a=-g;t=2sec

v=u+at

0=u-g×2

u=19.6m/s (upward direction)

(b)

From road, motion of ball will be projective

Now, usin θ=19.6

Ucos θ=14. 7

Squaring and adding

u²=(19.6)²+(14.7)²

u=25m/s

On dividing,

Tan θ=

θ=53°

Solution 44

Let ball lands on the nth bench

∴ y=(n-1)

and x=110+(n-1) = 110+y

Now

Y=x tan θ -

(n-1)=(110+n-1)tan53° -g

Solving

n=6

Solution 45

For near point of boat

R=5m= g

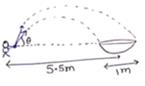
θ=15° or 75°

For for point of boat

R=6m=

θ=18° or 71°

For a successful shot angle may vary from 15° to 18° or 71° to 75°

Minimum angle=15°

Maximum angle=75°

Rest and Motion Kinematics Exercise 54

Solution 46

(a)

Velocity responsible for crossing is 10m/s

So, time to cross river=

t==40sec

(b)

Velocity responsible for drift=2m/s

Distance=speed × time

=2×40=80m

Solution 47

(a) Velocity responsible for crossing=3sinθ kmph

=3× sinθ

Time to cross=

= =

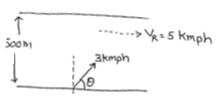
= minutes

(b) For t_min; sinθ=1

When θ=90°

t_min=10minutes

Solution 48

When v_river> v_manand for minimum drift sinθ=

sinθ=

θ=37°

Time to cross river=

drift=speed × time

=(5-3sin37°)time

=(5-d)()

drift= km

Solution 49

(a)

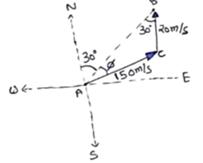
In ΔACB

Using sin formula

sin∅=

∅=sin^-1() east of the line AB

(b)

∅=3°48'. Angle between two vector=30 +3°48'

= (150)²+(20)²+2(150)(20)cos33°.48'

R=167m/s

Time==

=2994 sec

T=≈50min

Solution 50

Initially, resultant velocity of sound=v+u

(v+u)= ----(i)

Later, resultant velocity of sound=v-u

(v-u)= ------(ii)

Add (i) and (ii)

V=(+)

and

u=(-)

Solution 51

Let v be the velocity of sound along direction AC so it can reach B with resultant velocity AD

Velocity along AB=

Time=

Solution 52

Relative velocity = v-vcosθ

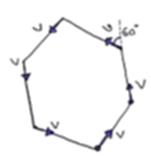
S_rel=a

Speed=

Please Login or Sign up to continue!

Class 11-science H C VERMA Solutions Physics Chapter 3: Rest and Motion Kinematics

Rest and Motion Kinematics Exercise 51

Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Rest and Motion Kinematics Exercise 52

Solution 11

Solution 12

Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18

Solution 19

Solution 20

Solution 21

Solution 22

Solution 23

Solution 24

Solution 25

Solution 26

Rest and Motion Kinematics Exercise 53

Solution 27

Solution 28

Solution 29

Solution 30

Solution 31

Solution 32

Solution 33

Solution 34

Solution 35

Solution 36

Solution 37

Solution 38

Solution 39

Solution 40

Solution 41

Solution 42

Solution 43

Solution 44

Solution 45

Rest and Motion Kinematics Exercise 54

Solution 46

Solution 47

Solution 48

Solution 49

Solution 50

Solution 51

Solution 52

Get in Touch