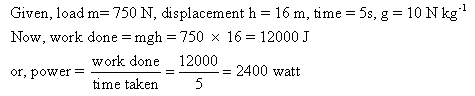Class 10 FRANK Solutions Physics Chapter 1.4 - Work, Energy, Power and Their Relation with Force

Access Frank Solutions for ICSE Class 10 Physics Chapter 1.4 Work, Energy, Power and their Relation with Force at TopperLearning. Revise chapter terms such as work, power, watt, joule and more through our Physics solutions. Find out whether work done is a vector quantity or a scalar quantity. Through the chapter solutions, our experts also guide you in solving simple calculations on work done using the relevant formula.

In addition, practise important ICSE Class 10 Physics MCQs from this chapter through our online practice tests. You could also revise important Physics chapter concepts with our study materials like concept videos, question papers, Selina Solutions etc.

Work, Energy, Power and Their Relation with Force Exercise 37

Solution 1

Force

Solution 2

Yes

Solution 3

Joule

Solution 4

Work

Solution 5

1N, 1m in its own direction

Solution 6

When no net force is applied, the work done which is the dot product of force and displacement is zero.

Work, Energy, Power and Their Relation with Force Exercise 38

Solution 7

The work done is zero because the displacement is zero.

Solution 8

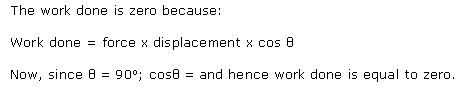
Solution 9

Work is a scalar quantity because it is a measure of transfer of energy without indicating any direction.

Solution 10

Solution 11

The work done by the gravitational force of the earth on a satellite revolving around the earth is zero because the motion of the satellite is perpendicular to the force at every point.

Solution 12

Solution 13

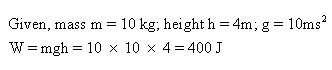
Solution 14

The work done against gravity is zero when a body is moved horizontally along a frictionless surface because the force of gravity is perpendicular to the displacement in this case.

Solution 15

'Work' is said to be done when the applied force makes the body move i.e., there is a displacement of body.
It is equal to the product of force and the displacement of the point of application of the force in the direction of force.

Solution 16

Work done depends upon:
(i) the magnitude and direction of the applied force, and
(ii) the displacement it produces.

Solution 17

Yes, we perform work against gravity.

Solution 18

The angle should be 90^o.

Solution 19

This is because at each point of the circular path, the displacement is perpendicular to the force, which is directed towards the centre, along the radius.

Solution 20

When the angle between the direction of motion and that of the force is 90°;
W = Fd cos 90° = 0
When the angle between the direction of motion and that of the force is 0°;
W = Fd cos 0° = Fd
Hence in the second case, when the angle is 0°; the work done is more.

Solution 21

The displacement of the man and suitcase is along the horizontal direction. Thus, the angle between the displacement and the force of gravity is 90°;
Thus, W = Fd cos 90° = 0
Hence, no work is done against gravity in this case.

Solution 22

When a body moves along a circular path, work done by the gravitational force towards the centre of the path is zero, because the displacement in this case is normal to the gravitational force.

Solution 23

The work done by the gravitational force of the sun on earth during its motion around the sun is zero because at every point, the displacement of earth is perpendicular to the gravitational force of sun i.e.,
W = Fd cos 90⁰ = 0

Solution 24

A kilojoule of work is said to done when a force of 1 newton displaces a body through 1000 metres in its own direction.
1 kJ = 10³ joules

Solution 25

1 MJ = 10⁶ joules

Solution 26

The SI unit of work is joule.
1 joule of work is said to be done when a force of 1 newton displaces a body through 1 metre in its own direction.

Solution 27

The SI unit of work is 'joules' and the CGS unit is 'erg'.
1 joule = 10⁷ erg
Thus the ratio is 10⁷: 1

Solution 28

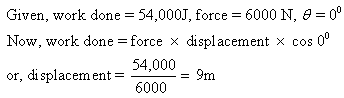
Solution 29

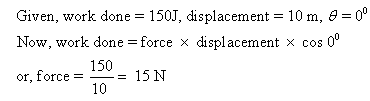
Solution 30

Applied force, displacement in the direction of the applied force.

Solution 31

Examples of work done:
(i) In free fall of a body of mass m, under gravity from a height h, the force of gravity (F=mg) is in the direction of displacement (=h) and the work done by the gravity is mgh.
(ii) A coolie lifting a load does work against gravity.

Solution 32

Work done depends upon:
(i) the magnitude and direction of the applied force, and
(ii) the displacement it produces.

Solution 33

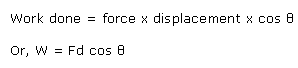
Solution 34

Work done against gravity = mass x acceleration due to gravity x height
Or, W = mgh

Solution 35

The displacement of the man and box is along the horizontal direction. Thus, the angle between the displacement and the force of gravity is 90⁰;
Thus, W = Fd cos 90⁰ = 0
Hence, no work is done against gravity in this case; however some work is done against friction.

Solution 36

Yes, power is a scalar quantity.

Solution 37

No, every force cannot produce work. Force can produce work if the applied force cause displacement in the direction of the force.

Solution 38

Work is said to be done only when the applied force on a body makes the body move but power is the rate of doing work.
The SI unit of work is 'joules' and that of power is 'watt'.

Solution 39

(a) joule, watt
(b) power, energy
(c) work
(d) 10⁷
(e) 746

Solution 40

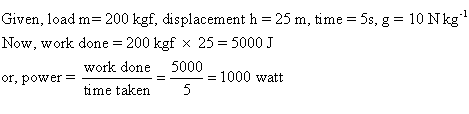
Work, Energy, Power and Their Relation with Force Exercise 39

Solution 43

Work done depends upon the vertical height and not the path taken, hence if the boy uses a lift to reach the same vertical height, work done will be mgh.

Solution 44

Yes, for e.g. if you push a wall, you apply force on it but no work is done since the displacement is zero.

Solution 45

1 H.P. = 0.746 kW

Solution 46

Solution 47

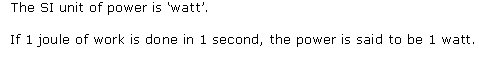
Solution 48

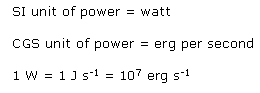
Solution 41

Solution 42

Power

Please Login or Sign up to continue!