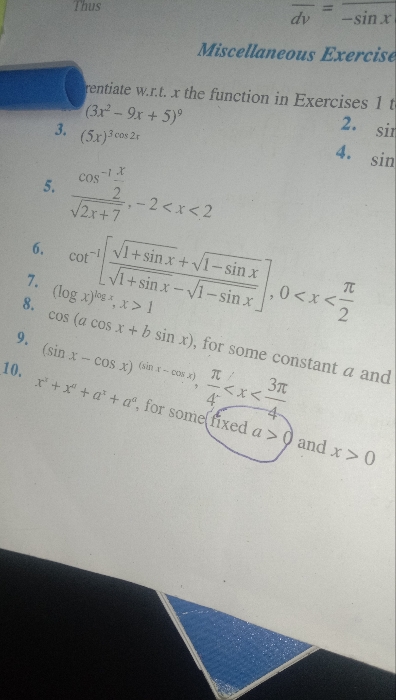CBSE Class 12-science Answered
Q1.prove that maximum area of right triangle inscribed in a circle is isosceles
Asked by | 06 Mar, 2009, 08:46: PM
Given a circle with radius r.
Let triangle ABC be a right triangle inscribed in the circle.
Since the triangle is a right triangle, hence one of the angle is 90o.
Let angle C = 90o
Then AB is diameter of the circle, since angle in semi circle is 90o
Hence, AB= 2r, let BC=x and AC = y
Area of traingle ABC = A = 1/2 * x*y
Applying pythagoras theorem in triangle ABC, we het
y =  ((2r)2-x2) =
((2r)2-x2) =  (4r2-x2)
(4r2-x2)
Putting this value of y in area
A = 1/2 * x *  (4r2-x2)
(4r2-x2)
Differentiating A with respect to x, we get
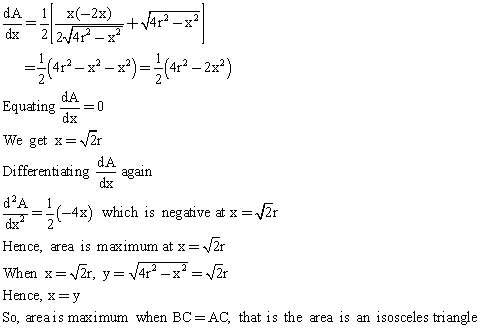
Answered by | 20 Mar, 2009, 12:38: PM
Application Videos
Concept Videos
CBSE 12-science - Maths
Asked by leelasri11663 | 25 Apr, 2024, 11:34: AM
CBSE 12-science - Maths
Asked by aishaazmata | 24 Apr, 2024, 08:48: PM
CBSE 12-science - Maths
Asked by revengesena | 24 Apr, 2024, 06:08: PM
CBSE 12-science - Maths
Asked by mahammadsharifdakhani67 | 16 Apr, 2024, 07:43: PM
CBSE 12-science - Maths
Asked by 20muskaansharma23 | 08 Apr, 2024, 11:31: AM
CBSE 12-science - Maths
Asked by cherrycharishma512 | 01 Apr, 2024, 12:32: PM
CBSE 12-science - Maths
Asked by annapoornaa429 | 31 Mar, 2024, 08:23: PM
CBSE 12-science - Maths
Asked by shirishakuruva477 | 28 Mar, 2024, 09:52: PM