CBSE Class 10 Answered
prove that 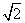 is irrational number.
is irrational number.
Asked by Topperlearning User | 12 Dec, 2013, 01:40: AM
Let us assume, to the contrary that ![]() is rational
is rational
![]() =
=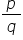
or ![]()
![]() --- (1)
--- (1)
Therefore 2 divides ![]() and 2 divides p. So we can
and 2 divides p. So we can
write p = 2r for some integer r
Substituting this value of p = 2r in (1)
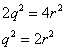
This means 2 divides to ![]() or 2 divides q also. Therefore, p and q have at least 2 as a common factor. But this contradict the fact that p and q have no common factor other than 1.
or 2 divides q also. Therefore, p and q have at least 2 as a common factor. But this contradict the fact that p and q have no common factor other than 1.
This contradiction arises because of our wrong assumption that ![]() is a rational number. So we conclude that
is a rational number. So we conclude that ![]() is irrational number.
is irrational number.
Answered by | 12 Dec, 2013, 03:40: AM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by nagalaxmidurgarao937 | 08 Apr, 2024, 01:42: PM
CBSE 10 - Maths
Asked by reddyjaswamth | 10 Jan, 2024, 01:49: PM
CBSE 10 - Maths
Asked by pv925403 | 07 Jan, 2024, 07:32: PM
CBSE 10 - Maths
Asked by abdulqadirmohd028 | 22 Dec, 2023, 12:56: AM
CBSE 10 - Maths
Asked by appanaboinakhasim8 | 05 Dec, 2023, 07:01: PM
CBSE 10 - Maths
Asked by kanchandevi5268 | 03 Nov, 2023, 06:35: AM
CBSE 10 - Maths
Asked by appusingh0840 | 29 Oct, 2023, 01:14: PM
CBSE 10 - Maths
Asked by jilsmendapara123 | 28 Jul, 2023, 02:44: PM








