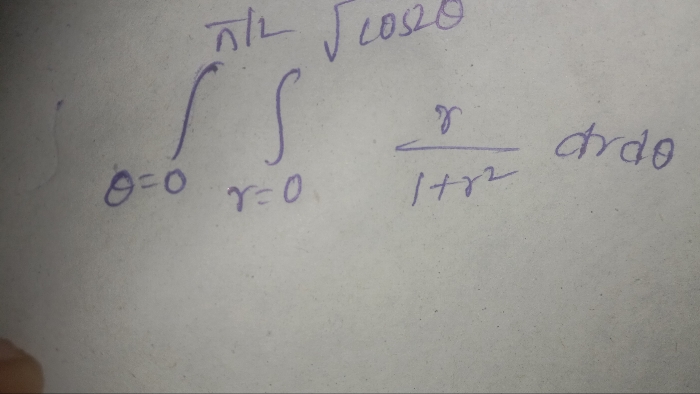CBSE Class 12-science Answered
Integrate the given ques
Asked by spsberry8 | 02 Feb, 2011, 07:49: PM
Dear student,
sinx + cosx = √2.sin(x+∏/4)
So, log(sinx + cosx) = log[√2.sin(x+∏/4)]
= log√2 + logsin(x+∏/4)
We have:
So, log(sinx + cosx) = log[√2.sin(x+∏/4)]
= log√2 + logsin(x+∏/4)
We have:
I = ∫log√2 dx + ∫logsin(x+∏/4) dx
= (log√2)x + I'
In I', put x+∏/4 = t. So, dx = dt
= (log√2)x + I'
In I', put x+∏/4 = t. So, dx = dt
I' = ∫log(sint) dt
Now, the limit is 0 to ∏/2
So, I = ∏/2.log√2 + I', where the limits are from o to ∏/2 ... (A)
Now, the limit is 0 to ∏/2
So, I = ∏/2.log√2 + I', where the limits are from o to ∏/2 ... (A)
Now, I'=∫ log(sin x).dx ...(1)
I'=∫logsin(π/2-x)dx
I'=∫logcosx dx...(2)
Add1&2,
2I'=∫logsinx+logcosx dx
=∫logsinx*cosx dx
=∫log(sin2x)/2 dx
=∫[logsin2x-log2] dx
=∫logsin2xdx - ∫log2dx ...(3)
In the first integral put 2x=t so dx=dt/2
when x=0,t=0 when x=π/2 ,t=π
So, the first integral can be solved as below:
∫logsint dt with limit t= o & t=π
Now, solve this integral and get the value of the integral I' from the equation (3). Thereafter, equate the value of I' in (A) to get the value of the required integral I.
Now, solve this integral and get the value of the integral I' from the equation (3). Thereafter, equate the value of I' in (A) to get the value of the required integral I.
We hope that clarifies your query.
Regards,
Team
TopperLearning
Answered by | 23 Mar, 2011, 09:25: PM
Concept Videos
CBSE 12-science - Maths
Asked by jprathamesh023 | 23 Mar, 2024, 04:01: PM
CBSE 12-science - Maths
Asked by atulmishra514 | 26 Jan, 2024, 10:15: PM
CBSE 12-science - Maths
Asked by aalavarshitha2005 | 21 Jan, 2024, 05:28: PM
CBSE 12-science - Maths
Asked by atharvaparkar04 | 17 Dec, 2023, 12:59: PM
CBSE 12-science - Maths
Asked by shashinayaka032 | 05 Dec, 2023, 12:46: PM
CBSE 12-science - Maths
Asked by manyarajawat1 | 06 Nov, 2023, 05:03: PM
CBSE 12-science - Maths
Asked by ps9680677 | 26 Oct, 2023, 11:47: AM
CBSE 12-science - Maths
Asked by manasvichandel49 | 19 Oct, 2023, 08:53: AM