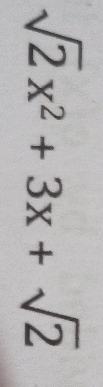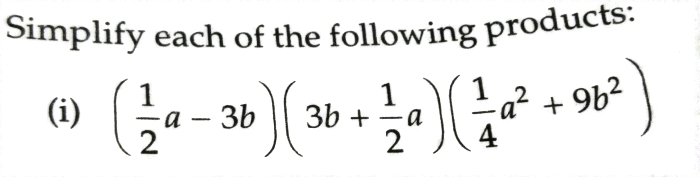CBSE Class 9 Answered
Factor theorem
In algebra, the factor theorem is a theorem for finding out the factors of a polynomial (an expression in which the terms are only added, subtracted or multiplied, e.g. x2 + 6x + 6). It is a special case of the polynomial remainder theorem.
The factor theorem states that a polynomial f(x) has a factor x − k if and only if f(k) = 0.
You wish to find the factors of
- x3 + 7x2 + 8x + 2.
To do this you would use trial and error finding the first factor. When the result is equal to 0, we know that we have a factor. Is (x − 1) a factor? To find out, substitute x = 1 into the polynomial above:
- x3 + 7x2 + 8x + 2 = (1)3 + 7(1)2 + 8(1) + 2
- = 1 + 7 + 8 + 2
- = 18
As this is equal to 18—not 0—(x − 1) is not a factor of x3 + 7x2 + 8x + 2. So, we next try (x + 1) (substituting x = − 1 into the polynomial):
- ( − 1)3 + 7( − 1)2 + 8( − 1) + 2.
This is equal to 0. Therefore x − ( − 1), which is to say x + 1, is a factor, and -1 is a root of x3 + 7x2 + 8x + 2.
The next two roots can be found by algebraically dividing x3 + 7x2 + 8x + 2 by (x + 1) to get a quadratic, which can be solved directly, by the factor theorem or by the quadratic equation.  = x2 + 6x + 2 and therefore (x + 1) and x2 + 6x + 2 are the factors of x3 + 7x2 + 8x + 2.
= x2 + 6x + 2 and therefore (x + 1) and x2 + 6x + 2 are the factors of x3 + 7x2 + 8x + 2.