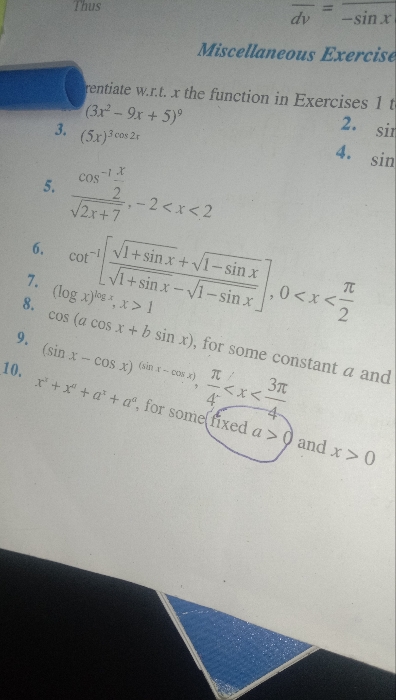CBSE Class 12-science Answered
For any sqare matrix A prove that A+A' is a symmetric matrix
Asked by neesa.vs | 17 Mar, 2017, 05:37: PM

Answered by | 17 Mar, 2017, 09:27: PM
Application Videos
Concept Videos
CBSE 12-science - Maths
Asked by leelasri11663 | 25 Apr, 2024, 11:34: AM
CBSE 12-science - Maths
Asked by aishaazmata | 24 Apr, 2024, 08:48: PM
CBSE 12-science - Maths
Asked by revengesena | 24 Apr, 2024, 06:08: PM
CBSE 12-science - Maths
Asked by mahammadsharifdakhani67 | 16 Apr, 2024, 07:43: PM
CBSE 12-science - Maths
Asked by 20muskaansharma23 | 08 Apr, 2024, 11:31: AM
CBSE 12-science - Maths
Asked by cherrycharishma512 | 01 Apr, 2024, 12:32: PM
CBSE 12-science - Maths
Asked by annapoornaa429 | 31 Mar, 2024, 08:23: PM
CBSE 12-science - Maths
Asked by shirishakuruva477 | 28 Mar, 2024, 09:52: PM