CBSE Class 9 Answered
A point E is taken as the midpoint of the
side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove
that ar ( ADF) = ar(ABFC).
ADF) = ar(ABFC).
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
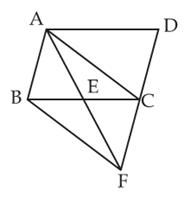
In triangles ABE and CFE,
BE = CE (E is the mid-point of BC)
![]() (vertically opposite angles)
(vertically opposite angles)
![]() (AB||CD and CD is produced to CF)
(AB||CD and CD is produced to CF)
![]()
![]() ABE
ABE
![]()
![]() FCE (ASA
criteria)
FCE (ASA
criteria)
![]() AB
= CF
AB
= CF
Now, AB = CD, as ABCD is a parallelogram.
Therefore, AB = CF = CD
![]() C is midpoint of FD
C is midpoint of FD
In parallelogram ABFC, AF is the diagonal, therefore,
ar(![]() ABF) = ar(
ABF) = ar(![]() ACF) ……(i)
ACF) ……(i)
In
![]() ADF,
ADF,
AC is the median, since CD = CF
Therefore,
ar(![]() ACF) = ar(
ACF) = ar(![]() ACD) ……(ii)
ACD) ……(ii)
From (i) and (ii)
ar(![]() ABF) = ar(
ABF) = ar(![]() ACD)
ACD)
Adding
ar(![]() ACF) to both sides,
ACF) to both sides,
ar(![]() ABF) + ar(
ABF) + ar(![]() ACF) = ar(
ACF) = ar(![]() ACD) + ar(
ACD) + ar(![]() ACF)
ACF)
ar(||gm
ABFC) = ar(![]() ADF)
ADF)
Answered by | 04 Jun, 2014, 03:23: PM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by bascaljoseph | 07 Feb, 2023, 01:27: PM
CBSE 9 - Maths
Asked by deepakumaraiya200 | 30 Jun, 2020, 09:51: AM
CBSE 9 - Maths
Asked by kishor.kp14 | 15 Dec, 2019, 05:00: PM
CBSE 9 - Maths
Asked by ravinderchoudhary0486 | 06 Dec, 2019, 10:59: AM
CBSE 9 - Maths
Asked by kumarvsteel477 | 12 Sep, 2019, 08:22: AM
CBSE 9 - Maths
Asked by phukansayan5 | 28 Aug, 2019, 06:16: PM
CBSE 9 - Maths
Asked by arunpssac | 19 Aug, 2019, 07:02: PM
CBSE 9 - Maths
Asked by yuvrajlkr8877 | 07 Aug, 2019, 09:31: PM
CBSE 9 - Maths
Asked by rushabhjain.av | 01 Apr, 2019, 07:56: AM
CBSE 9 - Maths
Asked by bhardwajvishesh2004 | 28 Nov, 2018, 04:18: PM





