Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

NEET Class neet Answered

Which of the following functions represent wave ? Plzz Explain each option by differential equation of wave... →d²y/dx²=1/v²(d²y/dt²)
question image
Asked by jhajuhi19 | 05 Mar, 2020, 13:28: PM
answered-by-expert Expert Answer
if a function y(x,t) is solution to the differential equation of wave motion , 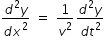 begin mathsize 14px style fraction numerator d squared y over denominator d x squared end fraction space equals space 1 over v squared fraction numerator d squared y over denominator d t squared end fraction end style 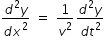 ..........................(1)
where v is speed of wave, then y(x,t) represents wave .
 
(a) y(x,t) = sin(kx) cos(ωt )
 
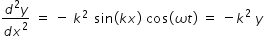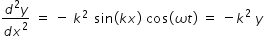we find,  begin mathsize 14px style fraction numerator d squared y over denominator d x squared end fraction space equals space minus space k to the power of 2 to the power of space end exponent space sin left parenthesis k x right parenthesis space cos left parenthesis omega t right parenthesis space equals space minus k squared space y end style ...........................(2)
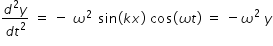we find begin mathsize 14px style fraction numerator d squared y over denominator d t squared end fraction space equals space minus space omega to the power of 2 to the power of space end exponent space sin left parenthesis k x right parenthesis space cos left parenthesis omega t right parenthesis space equals space minus omega squared space y end style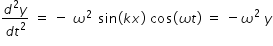.......................(3)
In above equations ω is angular frequency and k is wave vector .
 
Speed of the wave v is related to angular frequency ω and wave vector k is ,  v = ω/k  ..................(4)
 
from eqns.(2) , (3) and (4), we verify the function y(x,t) = sin(kx) cos(ωt) is solution to the differential equation
of wave motion as given by eqn.(1).
 
hence the function y(x,t) represents wave
---------------------------------------------------------------------------
 
(b) y(x,t) = k2 x2 - ω2 t2
 
we find , begin mathsize 14px style fraction numerator d squared y over denominator d x squared end fraction space equals space 2 space k to the power of 2 to the power of space end exponent space space end style  and    begin mathsize 14px style fraction numerator d squared y over denominator d x squared end fraction space equals space minus 2 space omega to the power of 2 to the power of space end exponent space space end style
from the above relations we find y(x,t) = k2 x2 - ω2 t2 is not the solution of differential equation (1)
 
Hence y(x,t) = k2 x2 - ω2 t2 do not represent wave
-------------------------------------------------------
 
similarly we can verify for other functions
 



Answered by Thiyagarajan K | 05 Mar, 2020, 19:24: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
NEET neet - Physics
what is the definition of OHM's law
Asked by deepakkumawat7886 | 30 Jan, 2025, 13:59: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
what is meant by projectile
Asked by sayrapatelsp09 | 04 Dec, 2024, 20:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
3 masses of 16 kg and 8 kg and 4 kg are placed in contact as shown in the figure if a force of 140 newton is applied on 4 KG mass, then the force on 16kg will be
Asked by jhansikethburugu2008 | 04 Oct, 2024, 22:09: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
RMS velocity for certain di atomic at 27°c is 1930 find the gas
Asked by arfasamreen7766 | 13 Sep, 2024, 16:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
at thin wire has length of 21.7cm and radius 0.46mm calculate the volume of the wire to connect significant figures
Asked by mehekfz8738 | 02 Sep, 2024, 19:56: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
explain nature of magnetic field lines
Asked by muhammadifatimanoori | 22 Aug, 2024, 09:10: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
a parallel plate capacitor is charged up to a potential V distance between the plates is d. electric field intensity between the plates is E. if the distance between plates is doubled then the electric field will be
Asked by kumawatranya0812 | 16 Aug, 2024, 16:25: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
hailstones fall from a certain height if only 1% of the hailstones melt on reaching the ground find the height from which they fall
Asked by nzf1042692 | 10 Aug, 2024, 21:07: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
The position function of a particle moving along the x axis is x(t t 2 3t 2) time t=0 to t =3 find distance travelled
Asked by dropper744 | 08 Aug, 2024, 10:44: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
Ek pahiya 120 Chakkar Prati minut se ghoom raha hai to ghumte pahiye ki koniya Sal Hogi
Asked by sajnadevirrc | 06 Aug, 2024, 11:55: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt