CBSE Class 12-science Answered

The value of direction cosine of two straight lines can satisfy the two equation, 3l+m+5n=0 & 6mn-2nl+5lm=0 . Find the angle between those lines.

Asked by rsjkumar2003 | 23 Sep, 2019, 01:09: PM

Expert Answer

3l+m+5n=0 i.e. m=-(3l+5n) .... (i)

6mn-2nl+5lm=0 ... (ii)

Substituting m in the (ii) eq, we get

(l+n)(l+2n)=0

l=-n or l=-2n

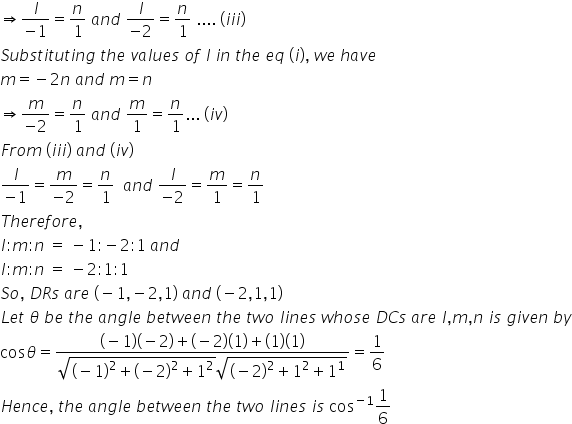
rightwards double arrow fraction numerator l over denominator negative 1 end fraction equals n over 1 space a n d space fraction numerator l over denominator negative 2 end fraction equals n over 1 space.... space left parenthesis i i i right parenthesis S u b s t i t u t i n g space t h e space v a l u e s space o f space l space i n space t h e space e q space left parenthesis i right parenthesis comma space w e space h a v e m equals negative 2 n space a n d space m equals n rightwards double arrow fraction numerator m over denominator negative 2 end fraction equals n over 1 space a n d space m over 1 equals n over 1... space left parenthesis i v right parenthesis F r o m space left parenthesis i i i right parenthesis space a n d space left parenthesis i v right parenthesis fraction numerator l over denominator negative 1 end fraction equals fraction numerator m over denominator negative 2 end fraction equals n over 1 space space a n d space fraction numerator l over denominator negative 2 end fraction equals m over 1 equals n over 1 T h e r e f o r e comma l colon m colon n space equals space minus 1 colon negative 2 colon 1 space a n d l colon m colon n space equals space minus 2 colon 1 colon 1 S o comma space D R s space a r e space left parenthesis negative 1 comma negative 2 comma 1 right parenthesis space a n d space left parenthesis negative 2 comma 1 comma 1 right parenthesis L e t space theta space b e space t h e space a n g l e space b e t w e e n space t h e space t w o space l i n e s space w h o s e space D C s space a r e space l comma m comma n space i s space g i v e n space b y cos theta equals fraction numerator left parenthesis negative 1 right parenthesis left parenthesis negative 2 right parenthesis plus left parenthesis negative 2 right parenthesis left parenthesis 1 right parenthesis plus left parenthesis 1 right parenthesis left parenthesis 1 right parenthesis over denominator square root of left parenthesis negative 1 right parenthesis squared plus left parenthesis negative 2 right parenthesis squared plus 1 to the power of 2 end exponent end root square root of left parenthesis negative 2 right parenthesis squared plus 1 to the power of 2 end exponent plus 1 to the power of 1 end root end fraction equals 1 over 6 H e n c e comma space t h e space a n g l e space b e t w e e n space t h e space t w o space l i n e s space i s space cos to the power of negative 1 end exponent 1 over 6

Answered by Renu Varma | 24 Sep, 2019, 10:05: AM

Practice Test

Webinar

Pre Board Assessment

CBSE Class 12-science Answered

Concept Videos

CONTACT

CBSE Class 12-science Answered

Concept Videos

Choose Filters

Get in Touch