Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

JEE Class main Answered

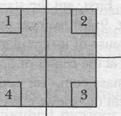
The figure shows a uniform square plate from which four identical squares at the corners will be removed. (a) Where is the center of mass of the plate originally? Where is it after the removal of (b) square 1; (c) squares 1 and 2; (d) squares 1 and 3; (e) squares 1, 2, and 3; (f) all four squares? Explain briefly 
question image
Asked by rushabh1234 | 21 Oct, 2019, 21:49: PM
answered-by-expert Expert Answer
centre of mass of full square plate is at geometrical centre O,
Let us have x-y coordinate system with origin O at centre of mass of full square plate.
 
(1) Square-1 is removed
 
By taking x-moment of masses with respect to O, we have
 
- a2 ρ [ (l/2)-(a/2) ] + (l2 - a2) ρ x = 0   or  x = (1/2) a2 /(l+a)
 
first term in above expression is x-moment of square-1 and second term is x-moment of [ full square - square-1 ]
ρ is mass per unit area and x is x-coordinate of centre of mass
 
Similarly by taking y-moment, we have
 a2 ρ [ (l/2)-(a/2) ] + (l2 - a2) ρ y = 0   or  y = -(1/2) a2 /(l+a)
 
Hence corrdinates of centre of mass from O :-  [ (1/2) a2 /(l+a), -(1/2) a2 /(l+a) ]
---------------------------------------------------------------------
Square-1 and square-2 are removed
 
By taking x-moment of masses with respect to O, we have
 
- a2 ρ [ (l/2)-(a/2) ] + a2 ρ [ (l/2)-(a/2) ] +  (l2 - 2a2) ρ x = 0   or  x = 0
 
first term in above expression is x-moment of square-1.  second term is x-moment of square-2 and
third term is x-moment of [ full square - square-1 - square-2]
 
Similarly by taking y-moment, we have
 a2 ρ [ (l/2)-(a/2) ] + a2 ρ [ (l/2)-(a/2) ]+ (l2 - 2a2) ρ y = 0   or  y = - a2(l-a) /(l2-2a2)
 
Hence corrdinates of centre of mass from O :-  [ 0 , - a2(l-a) /(l2-2a2) ]
-------------------------------------------------------------------------------
Square-1 and square-3 are removed
 
By taking x-moment of masses with respect to O, we have
 
- a2 ρ [ (l/2)-(a/2) ] + a2 ρ [ (l/2)-(a/2) ] +  (l2 - 2a2) ρ x = 0   or  x = 0
 
first term in above expression is x-moment of square-1.  second term is x-moment of square-3 and
third term is x-moment of [ full square - square-1 - square-3]
 
Similarly by taking y-moment, we have
 a2 ρ [ (l/2)-(a/2) ] - a2 ρ [ (l/2)-(a/2) ]+ (l2 - 2a2) ρ y = 0   or  y = 0
 
Hence corrdinates of centre of mass from O :-  [ 0 , 0 ]
-----------------------------------------------------------------------------------------------------
 
User is advised to do the remaining part of this problem as explained above
Answered by Thiyagarajan K | 22 Oct, 2019, 12:27: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
JEE main - Physics
a marble block of mass 2 kg lying on ice when a given velocity of 6 ms–1 is stopped by friction in 10 seconds then co efficient of friction is
Asked by sumalathamadarapu9 | 23 Oct, 2024, 22:06: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
show that the frequency of oscillations remain unchanged whether a mass attached to a spring is made to oscillate in the vertical or in the horizontal direction
Asked by py309649 | 13 Oct, 2024, 13:39: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Square of the time period of revolution of a planet is proportional to the cube of the mean distance between sun and planet. If mean distance is increased by 2% then percentage change in its time period is
Asked by coolskrish | 13 Oct, 2024, 12:50: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
two particles of mass m and 4m are initially actress the sad moving towards each other due to mutual gravitational force at an instantly of m is vî then at this instant the velocity of mass 4m is
Asked by midnightmoon3355 | 09 Oct, 2024, 09:09: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
what is the second law of thermodynamics
Asked by rambabunaidu4455 | 03 Oct, 2024, 16:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
what is the relation between drift velocity and mobility
Asked by ratchanavalli07 | 17 Sep, 2024, 07:46: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
A ball of mass m approaches a moving wall of infinite mass with speed v along the normal to the wall. The speed of the ball is u towards the ball. The speed of the ball after elastic collision with the wall is
Asked by yayashvadutta45 | 15 Sep, 2024, 19:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
a current of 2a is flowing through a conductor of length 22m bent in arc radius 5cm
Asked by adithireddy999 | 03 Sep, 2024, 09:35: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
two vectors vector a and vector B lie in one plane vector c lie in the different plane then vector a + vector b + vector c is
Asked by vaishalinirmal739 | 29 Aug, 2024, 18:07: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
What is impulse?
Asked by vradhysyam | 26 Aug, 2024, 17:17: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt