Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

JEE Class main Answered

solve
question image
Asked by sarveshvibrantacademy | 07 May, 2019, 11:38: AM
answered-by-expert Expert Answer
mirror equation after applying sign convention for convex mirror :- 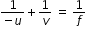 begin mathsize 12px style fraction numerator 1 over denominator negative u end fraction plus 1 over v space equals space 1 over f end style 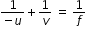 ................(1)
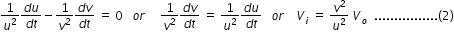
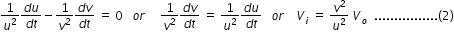
by differentiating eqn.(1) with respect to time,  begin mathsize 12px style 1 over u squared fraction numerator d u over denominator d t end fraction minus 1 over v squared fraction numerator d v over denominator d t end fraction space equals space 0 space space space o r space space space space space fraction numerator begin display style 1 end style over denominator begin display style v squared end style end fraction fraction numerator begin display style d v end style over denominator begin display style d t end style end fraction space equals space fraction numerator begin display style 1 end style over denominator begin display style u squared end style end fraction fraction numerator begin display style d u end style over denominator begin display style d t end style end fraction space space space o r space space space space V subscript i space equals space v squared over u squared space V subscript o space space................ left parenthesis 2 right parenthesis end style
where u is the object-to-lens distance, v is image-to-lens distance, f is focal length, Vo is the object speed and Vi is image speed .
 
let us eliminate v using eqn.(1) :  v = ( f u ) / (f+u)    or 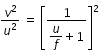 begin mathsize 12px style v squared over u squared space equals space open square brackets fraction numerator 1 over denominator begin display style u over f plus 1 end style end fraction close square brackets squared end style 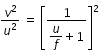..................(3)
from (2) and (3),  begin mathsize 12px style V subscript i space equals space open square brackets fraction numerator 1 over denominator begin display style u over f end style plus 1 end fraction close square brackets squared space V subscript o end style  ...................(4)
 
In eqn.(4), multiplier term on RHS is always >1 irrespective of  u < f   or u > f .  
Hence Vi < Vo irrespective of  u < f   or u > f .  Hence case (A) and case (C) are true
 
It can be verified from eqn.(4) that case (B) and (D) are false
Answered by Thiyagarajan K | 09 May, 2019, 10:19: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
JEE main - Physics
a marble block of mass 2 kg lying on ice when a given velocity of 6 ms–1 is stopped by friction in 10 seconds then co efficient of friction is
Asked by sumalathamadarapu9 | 23 Oct, 2024, 22:06: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
show that the frequency of oscillations remain unchanged whether a mass attached to a spring is made to oscillate in the vertical or in the horizontal direction
Asked by py309649 | 13 Oct, 2024, 13:39: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Square of the time period of revolution of a planet is proportional to the cube of the mean distance between sun and planet. If mean distance is increased by 2% then percentage change in its time period is
Asked by coolskrish | 13 Oct, 2024, 12:50: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
two particles of mass m and 4m are initially actress the sad moving towards each other due to mutual gravitational force at an instantly of m is vî then at this instant the velocity of mass 4m is
Asked by midnightmoon3355 | 09 Oct, 2024, 09:09: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
what is the second law of thermodynamics
Asked by rambabunaidu4455 | 03 Oct, 2024, 16:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
what is the relation between drift velocity and mobility
Asked by ratchanavalli07 | 17 Sep, 2024, 07:46: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
A ball of mass m approaches a moving wall of infinite mass with speed v along the normal to the wall. The speed of the ball is u towards the ball. The speed of the ball after elastic collision with the wall is
Asked by yayashvadutta45 | 15 Sep, 2024, 19:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
a current of 2a is flowing through a conductor of length 22m bent in arc radius 5cm
Asked by adithireddy999 | 03 Sep, 2024, 09:35: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
two vectors vector a and vector B lie in one plane vector c lie in the different plane then vector a + vector b + vector c is
Asked by vaishalinirmal739 | 29 Aug, 2024, 18:07: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
What is impulse?
Asked by vradhysyam | 26 Aug, 2024, 17:17: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt