Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

JEE Class main Answered

solve        
question image
Asked by sarveshvibrantacademy | 06 Apr, 2019, 15:00: PM
answered-by-expert Expert Answer
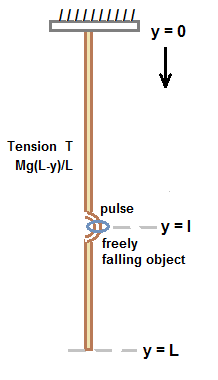
Let y be the distance measured from top of the rope towards bottom as shown in figure.
 
Tension T(y) at a point y of a rope is given by, T(y) = Mg(L-y)/L  .............................. (1)
 
where M is mass of rope and L is length of rope.
 
Veleocity of transverse wave, v(y) = 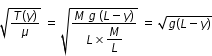begin mathsize 12px style square root of fraction numerator T left parenthesis y right parenthesis over denominator mu end fraction end root space equals space square root of fraction numerator M space g space open parentheses L minus y close parentheses over denominator L cross times begin display style M over L end style end fraction end root space equals space square root of g open parentheses L minus y close parentheses end root end style 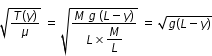  .........................(2)
where μ is linear mass density  i.e. mass per unit length.
 
let at time τ, the freely falling object meets the pulse at location y = l
 
then we have for freely falling object,  (1/2)gτ2 = l    or 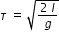begin mathsize 12px style tau space equals space square root of fraction numerator 2 space l over denominator g end fraction end root end style 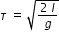......................(3)
Time τ required for the pulse to reach the location y = l is obtained  from eqn.(2) as follows
 
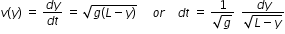begin mathsize 12px style v left parenthesis y right parenthesis space equals space fraction numerator d y over denominator d t end fraction space equals space square root of g open parentheses L minus y close parentheses end root space space space space space o r space space space space d t space equals space fraction numerator 1 over denominator square root of g end fraction space space fraction numerator d y over denominator square root of L minus y end root end fraction end style ................................(4)
integrating both sides of eqn.(4), we get, 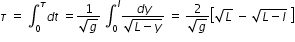begin mathsize 12px style tau space equals space integral subscript 0 superscript tau d t space equals fraction numerator 1 over denominator square root of g end fraction space integral subscript 0 superscript l fraction numerator d y over denominator square root of L minus y end root end fraction space equals space fraction numerator 2 over denominator square root of g end fraction open square brackets square root of L space minus space square root of L minus l end root space close square brackets end style 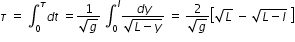 .......................(5)
By equating eqn.(3) and eqn.(5), and solving for l in terms of full length of rope L, we get l = (8/9)L
( user can verify the algebra, it is so long and difficult to enter all the steps involved )
 
hence from bottom, the pulse and the freely falling object meets at a distance (1/9)L
Answered by Thiyagarajan K | 07 Apr, 2019, 10:23: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
JEE main - Physics
a marble block of mass 2 kg lying on ice when a given velocity of 6 ms–1 is stopped by friction in 10 seconds then co efficient of friction is
Asked by sumalathamadarapu9 | 23 Oct, 2024, 22:06: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
show that the frequency of oscillations remain unchanged whether a mass attached to a spring is made to oscillate in the vertical or in the horizontal direction
Asked by py309649 | 13 Oct, 2024, 13:39: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Square of the time period of revolution of a planet is proportional to the cube of the mean distance between sun and planet. If mean distance is increased by 2% then percentage change in its time period is
Asked by coolskrish | 13 Oct, 2024, 12:50: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
two particles of mass m and 4m are initially actress the sad moving towards each other due to mutual gravitational force at an instantly of m is vî then at this instant the velocity of mass 4m is
Asked by midnightmoon3355 | 09 Oct, 2024, 09:09: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
what is the second law of thermodynamics
Asked by rambabunaidu4455 | 03 Oct, 2024, 16:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
what is the relation between drift velocity and mobility
Asked by ratchanavalli07 | 17 Sep, 2024, 07:46: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
A ball of mass m approaches a moving wall of infinite mass with speed v along the normal to the wall. The speed of the ball is u towards the ball. The speed of the ball after elastic collision with the wall is
Asked by yayashvadutta45 | 15 Sep, 2024, 19:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
a current of 2a is flowing through a conductor of length 22m bent in arc radius 5cm
Asked by adithireddy999 | 03 Sep, 2024, 09:35: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
two vectors vector a and vector B lie in one plane vector c lie in the different plane then vector a + vector b + vector c is
Asked by vaishalinirmal739 | 29 Aug, 2024, 18:07: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
What is impulse?
Asked by vradhysyam | 26 Aug, 2024, 17:17: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt