JEE Class main Answered
Sir please solve the mcq,provide steps...

Asked by subhrajayanta64 | 10 Sep, 2019, 04:37: AM
(Vectors are typed as Bold )
First, let us find out the magnetic field at test point r for the spinning charged sphere.
This is done by finding the magneteic vector potential A .
Then magnetic field is obtained from vector potential using B = 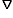 x A .
x A .
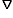 x A .
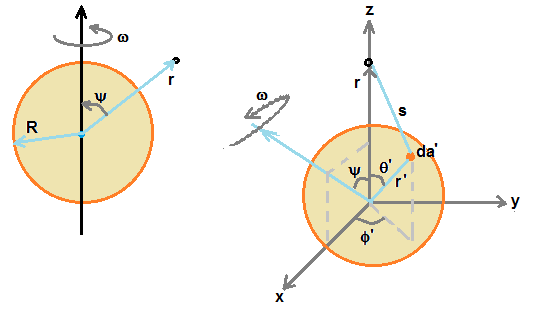
x A .Left side figure shows a charged sphere of radius R, spinning with angular speed ω .
It is required to find the vector potential at test point r whose position vctor makes angle ψ with the spinning axis.
Let us asume the coordinate system as shown in right side of figure so that centre of sphere coincides with origin,
position vector of test point r aligns with z-axis and spinning axis is rotated to lie in X-Z plane
Let us consider small area element da' = R2sinθ' dθ' dφ' . Vector potential dA at test point r is given by
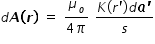 ........................(1)
........................(1)where K(r') is the surface current density, s is the ditance between area element da' and test point r.
vector potential A(r) due to whole spinning sphere, 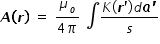 .................................(2)
.................................(2)
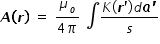 .................................(2)
.................................(2)we have, K(r') = σ v , and s = ( R2 + r2 - 2Rr cosθ' )
where σ is surface charge density, v is velocity vector of area element da'
we have,
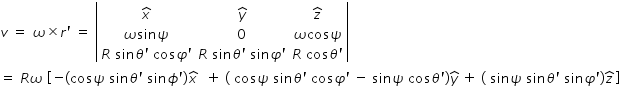
It has to be noticed that each of these terms, except one, involves either sinφ' or cosφ' .
Since integration of sinφ' or cosφ' within limits 0 to 2π vanishes, with only one non-vanishing term,
vector potential relation (2) becomes
 ........................ (3)
........................ (3)Above integration can be worked out using u = cosθ' , then integration eqn.(3) becomes
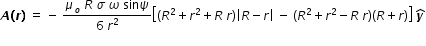 .....................................(4)
.....................................(4)Let us consider, ω × r = - ω r sinψ 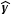 .
.
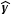 .
.Also when test point r is outside of sphere r > R, then bracketed term in eqn.(4) becomes -2R3
Hence 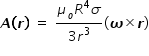 .................................(5)
.................................(5)
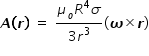 .................................(5)
.................................(5)Next step is to adjust the coordinate system, so that spinning axis coincides with z-axis and the point r is at (r, θ, φ)
Hence eqn.(5) becomes, 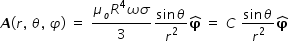 ..............................(6)
..............................(6)
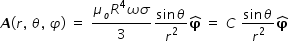 ..............................(6)
..............................(6)where in eqn.(6), C = ( μo R4 ω σ )/3 .............................(7)
Now to get magnetic field, we use B = 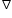 x A
x A
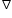 x A
x A In Spherical coordinate system, using curl of vector potential , magnetic field is written as,
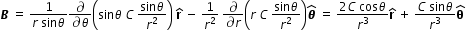 ......................................(8)
......................................(8)we know electric field of sphere at test point r,
E(r) = [ Q/(4πεor2) ] 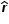 = [ (4πR2σ) / (4πεor2) ]
= [ (4πR2σ) / (4πεor2) ] 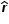 = [ (R2σ) / (εor2) ]
= [ (R2σ) / (εor2) ] 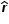 ........................(9)
........................(9)
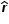 = [ (4πR2σ) / (4πεor2) ]
= [ (4πR2σ) / (4πεor2) ] 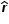 = [ (R2σ) / (εor2) ]
= [ (R2σ) / (εor2) ] 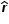 ........................(9)
........................(9)Poynting vector S = (1/μo) [ E × B ] = (1/μo) [ (R2σ) / (εor2) ] ( C sinθ / r3 ) 

By substituting C from eqn.(7), by considering r = R very near to spherical surface, Poynting vector becomes
S(θ) = [ (σ2 ω R sinθ )/εo ] 

Answered by Thiyagarajan K | 11 Sep, 2019, 12:27: PM
Application Videos
Concept Videos
JEE main - Physics
Asked by sumalathamadarapu9 | 23 Oct, 2024, 22:06: PM
JEE main - Physics
Asked by py309649 | 13 Oct, 2024, 13:39: PM
JEE main - Physics
Asked by coolskrish | 13 Oct, 2024, 12:50: PM
JEE main - Physics
Asked by midnightmoon3355 | 09 Oct, 2024, 09:09: AM
JEE main - Physics
Asked by rambabunaidu4455 | 03 Oct, 2024, 16:03: PM
JEE main - Physics
Asked by ratchanavalli07 | 17 Sep, 2024, 07:46: AM
JEE main - Physics
Asked by yayashvadutta45 | 15 Sep, 2024, 19:47: PM
JEE main - Physics
Asked by adithireddy999 | 03 Sep, 2024, 09:35: AM
JEE main - Physics
Asked by vaishalinirmal739 | 29 Aug, 2024, 18:07: PM
JEE main - Physics
Asked by vradhysyam | 26 Aug, 2024, 17:17: PM










