Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

JEE Class main Answered

Sir please provide answer to this question 
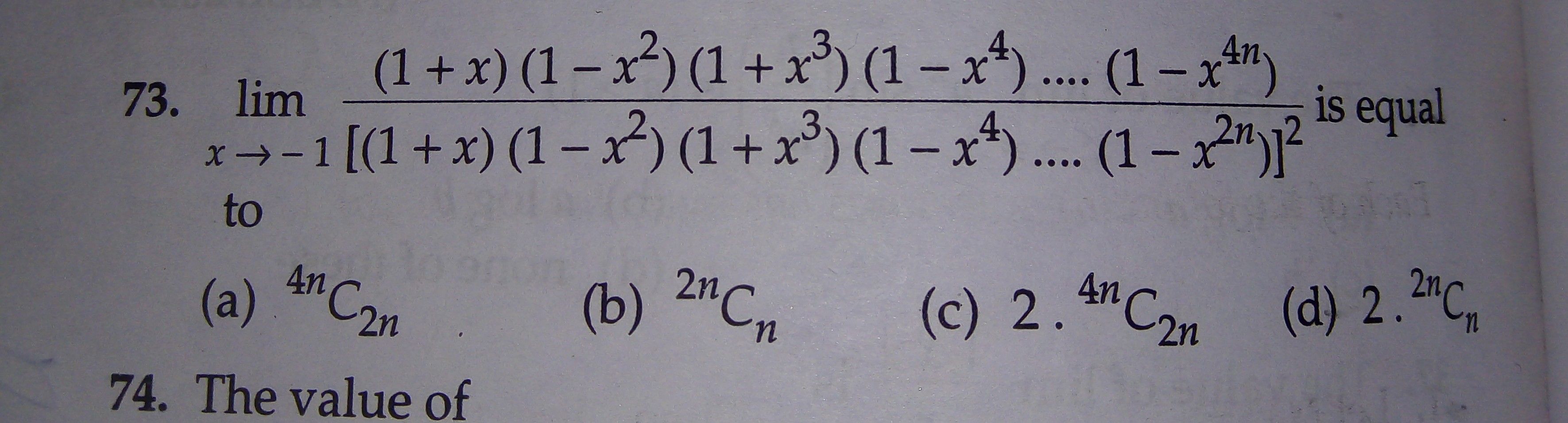
question image
Asked by anshuman.anshuman090 | 19 Sep, 2020, 12:05: PM
answered-by-expert Expert Answer
TO find the limit x tends to -1 for the function f(x) = {(1+x)(1-x2)(1+x3)(1-x4)...(1-x4n)}/{[(1+x)(1-x2)(1+x3)(1-x4)...(1-x2n)]2}
Cancel out the common terms in the numerator and denominator so we get 
f(x) = {(1+x2n+1)(1-x2n+2)(1+x2n+3)(1-x2n+4)...(1-x4n)}/{(1+x)(1-x2)(1+x3)(1-x4)...(1-x2n)}
Now use (a2 - b2) = (a - b)(a + b)
Again cancel out the common terms
Now substitute x = -1
If the value coming out to be 0, then again use the identity (a2 - b2) = (a + b)(a - b) and cancel out common terms
COntinue this till we get non-zero value
Answered by Renu Varma | 21 Sep, 2020, 19:38: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
JEE main - Maths
kho kho me kitne team khel sakte hain? options 1 6 2 4
Asked by amitraj39524 | 15 Feb, 2025, 05:15: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
find the equation of line passing through the point (3,2) and having slop 2
Asked by thosarrohit705 | 07 Feb, 2025, 18:08: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
If a number is completely divided by another number, can the quotient be an irrational number?
Asked by rathore6375 | 09 Jan, 2025, 10:52: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
in how many ways a team of 2 boys and 4 girls selected from 5 boys and 6 girls
Asked by pallavibirangal87 | 08 Dec, 2024, 10:18: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
if a chord of length 18 cm is 12 cm away from the centre then find the distance of 24 cm long chord from the centre
Asked by pritisindra6 | 06 Dec, 2024, 21:04: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
The number of ways in which at least one coin can be selected from 3 coins of one rupee, 4 coins of fifty paise, 5 coins of twenty paise and 6 coins of ten paise is-
Asked by kanishthkumawat | 29 Nov, 2024, 00:23: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
what is range of tan^-1 x
Asked by pawandhayal125 | 06 Oct, 2024, 10:03: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
what is 2+2
Asked by srishtipra2008 | 28 Sep, 2024, 10:33: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
n arithmetic means are inserted between the numbers 7 and 49. if the sum of these means is 364 then the sum of their squares is
Asked by yogeshsoni575 | 23 Sep, 2024, 23:01: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
consider a dodecagon then number of ways of selecting two triangles which can be made using the vertices of dodecagon so that they do not have a common side.
Asked by sumit.parsudih | 17 Sep, 2024, 22:22: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt