CBSE Class 10 Answered
Let us assume that ![]() is a rational;
is a rational;
![]() ,
,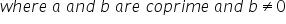
So, 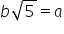
squaring both sides, we get
![]()
Therefore ![]() is divisible by 5 and also a is divisible by 5.
is divisible by 5 and also a is divisible by 5.
Now we can write 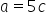 for some integer c.
for some integer c.
Substituting this value of for a, in (1) we get

This means that ![]() is divisible by 5 and also b is divisible by 5. Therefore a and b have 5 as their common factor, but this contradicts the fact that a and b are co prime. The contradiction arises because of our wrong assumption that
is divisible by 5 and also b is divisible by 5. Therefore a and b have 5 as their common factor, but this contradicts the fact that a and b are co prime. The contradiction arises because of our wrong assumption that ![]() is a rational.
is a rational.
So, we conclude that ![]() is an irrational.
is an irrational.








