Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

JEE Class main Answered

Plz sove my query as soon as possible shown below
question image
Asked by sarveshvibrantacademy | 16 Mar, 2019, 13:13: PM
answered-by-expert Expert Answer
when a stretched string under tension is fixed at both ends, standing waves are setup.
 
if y is displacment at any point x, then standing wave equation is given by,   y = 2a sin(kx) cos(ωt) ...........................(1)
 
for fundamental mode k = 2π/λ = 2π/(2L) = π/L  where λ is wavelength and L is length of string. 
 
ω = 2πf = 2π(v/λ) = πv/L , where f is frequency = v/λ  and v is velocity of wave in the string.
 
velocity at a given point x is given by, 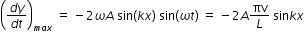 begin mathsize 12px style open parentheses fraction numerator begin display style d y end style over denominator begin display style d t end style end fraction close parentheses subscript m a x end subscript space equals space minus 2 omega A space sin left parenthesis k x right parenthesis space sin left parenthesis omega t right parenthesis space equals space minus 2 A πv over L space sin k x space end style 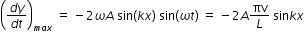.............................(2)
for a small mass of string dm at a point x, maximum kinetic energy dk is given by, 
 
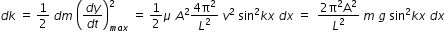begin mathsize 12px style d k space equals space 1 half space d m space open parentheses fraction numerator d y over denominator d t end fraction close parentheses subscript m a x end subscript superscript 2 space equals space 1 half mu space A squared fraction numerator 4 straight pi squared over denominator L squared end fraction space v squared space sin squared k x space d x space equals space space fraction numerator 2 straight pi squared straight A squared over denominator L squared end fraction space m space g space sin squared k x space d x end style   ................................(3)
where μ is the linear mass density (mass /unit length).
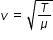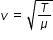we have used the relations  begin mathsize 12px style v space equals space square root of T over mu end root end style   and T = mg , to get the simplified eqn.(3)
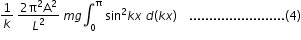
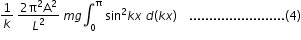
Maximum Kinetic energy Kmax for full string of length L  = begin mathsize 12px style 1 over k space fraction numerator begin display style 2 straight pi squared straight A squared end style over denominator begin display style L squared end style end fraction space m g integral subscript 0 superscript straight pi space sin squared k x space d left parenthesis k x right parenthesis space space space space........................ left parenthesis 4 right parenthesis end style
( integration limits :  when x = 0,   kx = 0  ;  when x = L,   kx = kL = π )
 
maximum kinetic energy Kmax is obtained from eqn.(4) ,  begin mathsize 12px style K subscript m a x end subscript space equals space fraction numerator straight pi squared straight A squared over denominator L end fraction space m space g end style
----------------------------------------
 
for first ovetone, maximum kinetic energy is calculated in similar manner by using   k = (2π) / λ =  (2π) / L 
Answered by Thiyagarajan K | 17 Mar, 2019, 11:55: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
JEE main - Physics
a marble block of mass 2 kg lying on ice when a given velocity of 6 ms–1 is stopped by friction in 10 seconds then co efficient of friction is
Asked by sumalathamadarapu9 | 23 Oct, 2024, 22:06: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
show that the frequency of oscillations remain unchanged whether a mass attached to a spring is made to oscillate in the vertical or in the horizontal direction
Asked by py309649 | 13 Oct, 2024, 13:39: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Square of the time period of revolution of a planet is proportional to the cube of the mean distance between sun and planet. If mean distance is increased by 2% then percentage change in its time period is
Asked by coolskrish | 13 Oct, 2024, 12:50: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
two particles of mass m and 4m are initially actress the sad moving towards each other due to mutual gravitational force at an instantly of m is vî then at this instant the velocity of mass 4m is
Asked by midnightmoon3355 | 09 Oct, 2024, 09:09: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
what is the second law of thermodynamics
Asked by rambabunaidu4455 | 03 Oct, 2024, 16:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
what is the relation between drift velocity and mobility
Asked by ratchanavalli07 | 17 Sep, 2024, 07:46: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
A ball of mass m approaches a moving wall of infinite mass with speed v along the normal to the wall. The speed of the ball is u towards the ball. The speed of the ball after elastic collision with the wall is
Asked by yayashvadutta45 | 15 Sep, 2024, 19:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
a current of 2a is flowing through a conductor of length 22m bent in arc radius 5cm
Asked by adithireddy999 | 03 Sep, 2024, 09:35: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
two vectors vector a and vector B lie in one plane vector c lie in the different plane then vector a + vector b + vector c is
Asked by vaishalinirmal739 | 29 Aug, 2024, 18:07: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
What is impulse?
Asked by vradhysyam | 26 Aug, 2024, 17:17: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt