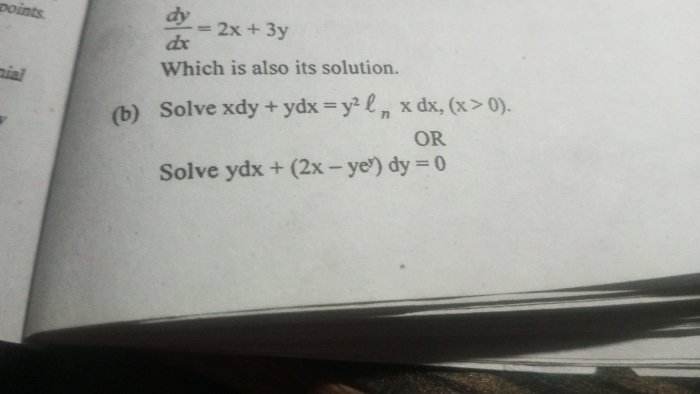CBSE Class 12-science Answered
Of all the closed cylindrical cans, which enclose a given volume has the minimum surface area?
Asked by | 07 Sep, 2009, 01:09: PM
Given volume = V
πr2h = V
h = V/πr2
S = total surface area = 2πr2 + 2πrh
= 2πr2 + 2πr(V/πr2)
= 2πr2 + 2V/r
To minimize the surface area,
dS/dr = 4πr - 2V/r2 = 0
d2S/dr2 = 4π + 4V/r3 > 0
2πr = V/r2
r = (V/2π)1/3
r = (100/2π)1/3
r = 2.52 cm and h = 5.02 cm.
The cylindrical can with r = 2.52 cm and h = 5.02 cm, will minimize the total surface area.
Regards,
Team,
TopperLearning.
Answered by | 07 Sep, 2009, 01:44: PM
Application Videos
Concept Videos
CBSE 12-science - Maths
Asked by aryaman822006 | 28 Apr, 2024, 11:52: AM
CBSE 12-science - Maths
Asked by vs.super.king999 | 28 Apr, 2024, 09:37: AM
CBSE 12-science - Maths
Asked by leelasri11663 | 25 Apr, 2024, 11:34: AM
CBSE 12-science - Maths
Asked by aishaazmata | 24 Apr, 2024, 08:48: PM
CBSE 12-science - Maths
Asked by revengesena | 24 Apr, 2024, 06:08: PM
CBSE 12-science - Maths
Asked by mahammadsharifdakhani67 | 16 Apr, 2024, 07:43: PM
CBSE 12-science - Maths
Asked by 20muskaansharma23 | 08 Apr, 2024, 11:31: AM
CBSE 12-science - Maths
Asked by cherrycharishma512 | 01 Apr, 2024, 12:32: PM