Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

NEET Class neet Answered

moment of inertia of a solid cylinder along an axis perpendicular to the axis of cylinder, we use parellel axis therom but i feel its wrong because the it can be applied only of the parellel axis pass through centre of mass of cylinder? can u please explain  
Asked by bhupinderpal61 | 10 Oct, 2019, 12:21: PM
answered-by-expert Expert Answer
Parallel axis theorem
 
 
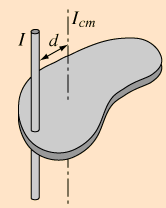
The moment of inertia of any object about an axis through its center of mass is the
minimum moment of inertia for an axis in that direction in space.
The moment of inertia about any axis parallel to that axis through the center of mass is given by 
 
Iparallel-axis = ICM + Md2
 
Your confusion is which axis is passing through centre of mass ?
 
Correct answer is reference axis is passing through centre of mass .
Using this reference axis passing through centre of mass, we are finding the moment of inertia about another parallel axis.
 
Hence parallel axis is not passing through centre of mass.
 
Moment of inertia of cylinder about an axis perpendicular to the axis of cylinder and passing through centre of mass is given below
 

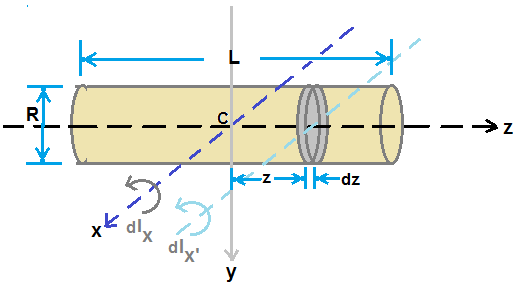
Let us consider a cylinder of radius R and length L and M be its mass.
 
Let the axis of cylinder coincides with z-axis of coordinate system.
We need to get moment of inertia about an axis perpendicular to axis of cylinder and passing throuh centre of mass of cylinder.
 
X-axis of coordinate system is the required axis of rotation as shown in figure.
 
Let us consider a thin disc of mass dm and thickness dz at a distance z frm centre of mass.
 
moment of inertia of this thin disk about axis of cylinder is given by
 
dIz = (1/2) dm R2  ..............(1)
 
By perpendicular axis theorem,   dIz = dIx' + dIy'   .............(2)
 
where x', y' axis are mutually perpendicular axis to z-axis . By symmetry, dIx' = dIy'
Hence dIx' = (1/2) dIz = (1/4) dm R2 ....................(3)
 
Moment of inertia given by above eqn. (3) is about the axis passing through centre of mass of thin disc.
 
Hence by parallel axis theorem, moment of inertia of this thin disc about the x-axis is given by
 
dIx = (1/4) dmR2 + dm z2................(4)
 
if mass is uniformly distributed, we have , dm = (M/L)dz   ..............(5)
 
using eqn.(5), eqn.(4) is rewritten as,   dIx = (1/4)R2(M/L)dz + (M/L) z2 dz  ..............(6)
 
Moment of inertia of whole cylinder about the x-axis is given by
 
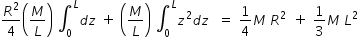
begin mathsize 14px style R squared over 4 open parentheses M over L close parentheses space integral subscript 0 superscript L d z space plus space open parentheses M over L close parentheses space integral subscript 0 superscript L z squared d z space space equals space 1 fourth M space R to the power of 2 space end exponent space plus space 1 third M space L squared end style

 

 


Answered by Thiyagarajan K | 12 Oct, 2019, 11:51: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
NEET neet - Physics
An object of mass 3 kg is at rest . Now if a force F=6t^2i+4tj is applied to the object what is the final velocity of the object after 3 second
Asked by cmashudrana | 26 Jul, 2024, 10:51: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
derive the equation of motions from vt graph
Asked by upparmanjunath70 | 19 Jul, 2024, 22:26: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
On the three corners of a square charge Q is kept and at the fourth corner charge q is kept. Find net electric force on charge q
Asked by zfaima704 | 19 Jul, 2024, 14:29: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
in a house three bulbs of 100w each are lighted for four hours daily and six tube lights of 20w each are lighted for five hours daily and a refrigerator of 400w is worked for 10hours daily for a month of 30days calculate the electricity bill if the cost of one unit is 4.00.
Asked by shaikmuneerjaan | 18 Jul, 2024, 20:58: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
An object is moving with variable speed then
Asked by nk4746870 | 15 Jul, 2024, 21:21: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
elevation of lift
Asked by dasmyton | 09 Jul, 2024, 22:46: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
a sonometer wire emits a fundamental note of frequency 150 hz calculate the frequency of note emitted when tension is change in the ratio of 9:16 and length of 1:2
Asked by shobhaguduru02 | 09 Jul, 2024, 20:21: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
speed of light in vacuum is 3 into 10 to the power 8 m/s if refractive index of glass is 1.5 the time taken by the light to travel 400 m in glass in microsecond is
Asked by kashinathpaikrao89446 | 09 Jul, 2024, 10:46: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
a body falls freely from a height it's average velocity when it reaches earth is
Asked by dshyamala44 | 08 Jul, 2024, 21:05: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
To a fish in water, a bird in air appears to be at 30 cm from the surface. If a
Asked by jagadishshnkr | 08 Jul, 2024, 20:50: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Are You a Teacher or a Parent Seeking Customised Tests? Click here
×