CBSE Class 9 Answered
MID PTS THEOREM
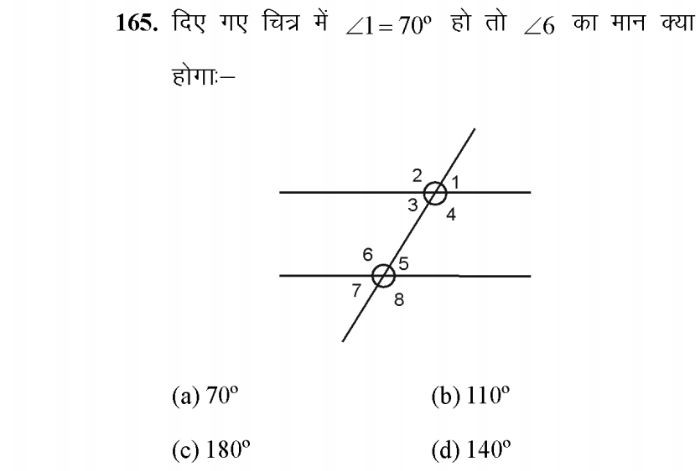
Asked by | 13 Sep, 2009, 06:46: AM
let ABCD is rectangle.
E,F,G,H be the mid points of the sides AB,BC,CD,DA resply.
join BD.
EH II BD
and
EH=1/2[BD].... mid pt thm.
simly
GFII BD
and
GF=1/2[BD]
So
EH=GF
and
EH II GF
so
EFGH is a parallelogram... one pair of opp sides is parallel and equal.
by the same argument as above,
we see that
EF=GH=1/2[AC]
but
BD=AC...Diagonals of a rectangle are equal.
so
EF=GH=1/2[AC]=1/2[BD]=EH=GF
so we see that for the parallelogram EFGH, all sides ae equal, so it's a rhombus.
Answered by | 13 Sep, 2009, 09:21: AM
Application Videos
Concept Videos
CBSE 9 - Maths
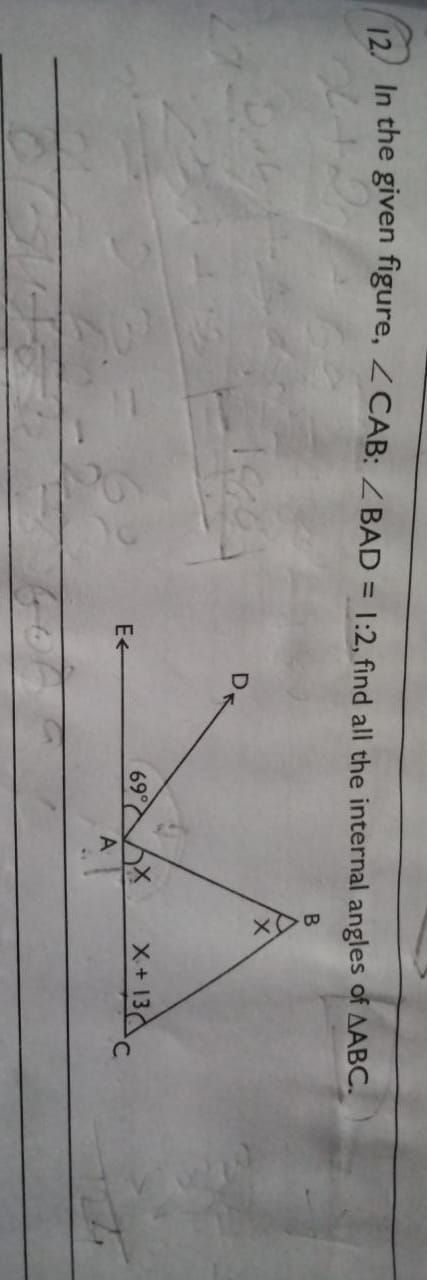
Asked by roshan.rony001 | 19 Sep, 2023, 05:02: PM
CBSE 9 - Maths
Asked by pushpadevipushpadevi19 | 13 Jan, 2023, 08:06: PM
CBSE 9 - Maths
Asked by savitamahajan202 | 02 Jan, 2023, 10:55: AM
CBSE 9 - Maths
Asked by amarjitruksh | 20 Jun, 2022, 10:40: PM
CBSE 9 - Maths
Asked by Abhishita9 | 12 Nov, 2021, 06:41: PM
CBSE 9 - Maths
Asked by raghavgargrg28 | 10 Sep, 2021, 05:11: PM
CBSE 9 - Maths
Asked by kamateganpati | 08 Sep, 2021, 06:17: PM
CBSE 9 - Maths
Asked by swatipuspapatel | 07 Feb, 2021, 07:29: PM
CBSE 9 - Maths
Asked by saritaagarwal30121980 | 14 Oct, 2020, 10:07: AM