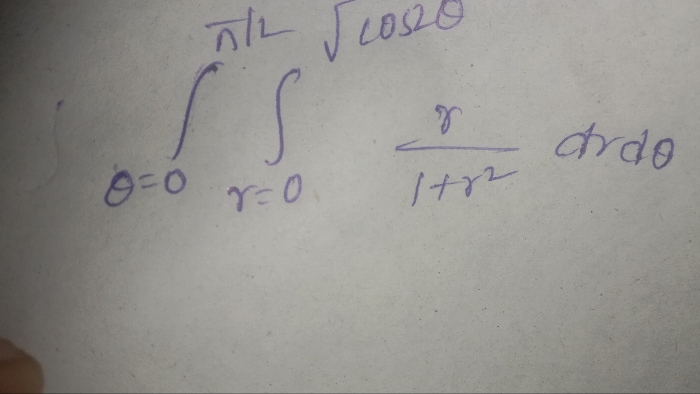CBSE Class 12-science Answered
Asked by manish.kkd4 | 20 Feb, 2019, 12:15: PM

Answered by Sneha shidid | 20 Feb, 2019, 01:07: PM
Concept Videos
CBSE 12-science - Maths
Asked by aalavarshitha2005 | 21 Jan, 2024, 05:28: PM
CBSE 12-science - Maths
Asked by atharvaparkar04 | 17 Dec, 2023, 12:59: PM
CBSE 12-science - Maths
Asked by shashinayaka032 | 05 Dec, 2023, 12:46: PM
CBSE 12-science - Maths
Asked by manasvichandel49 | 19 Oct, 2023, 08:53: AM
CBSE 12-science - Maths
Asked by diptiranigupta1981 | 02 Oct, 2023, 06:33: PM
CBSE 12-science - Maths
Asked by sdmbotch1123 | 30 Sep, 2023, 10:54: PM
CBSE 12-science - Maths
Asked by sdmbotch1123 | 16 Jan, 2023, 08:18: PM
CBSE 12-science - Maths
Asked by devilkano80 | 07 Jul, 2022, 01:45: PM