ICSE Class 9 Answered

Following steps to be followed to represent the irrational number on number line

Step.1 :-  Square of given irrational number should be expressed as sum of square numbers

Step 2 : Form a right triangle with above square root of square numbers as sides  so that square root of one square number

              is on number line and square 2of the other one is perpendicular to number line.

Step 3 :- join the hypotenuse of the right triangle formed . This length of hypotenuse represents the irrational number .

Step 4 :- Draw the arc with radius equal to hypotenuse and let the rac will meet a point on number line.

               This intersection point of arc with umber line represents the irrational number.

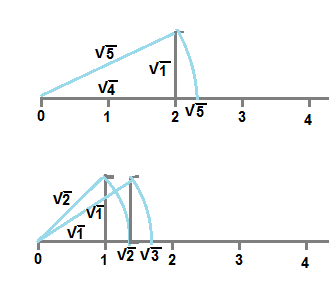
For example top figure of the illustration below shows above procedure to get irrational number √5 on number line .

For √5 , we write  5 = 4 + 1 = 2² + 1² .

Hence 4 and 1 are the square numbers so that perfect square root can be obtained.

Hence we make right triangle with side √4 on number line and side √1 perpendicular to number line .

Hypotenuse is 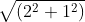= √5

If the square of given irrational number can not be written as perfect square numbers but it is written as sum of

square of irrational number and another perffect square number , then get the irrational number on number line .

Then form the right triangle with one side as this irrational number and other side as square root of other square number.

Then length of hypotenuse of second right triangle represents the irrational number .

For example we want to represent √3 as shown in the bottom figure of above illustration.

we first write , 3 = 2 + 1

1 is perfect square number because √1 = 1

but 2 is not a perfect square number and that itself an irrational number .

hence first get √2 on number line as described before.

Then use the right triangle with side √2 on number line and side 1 perpendicular to number line.

Hypotenuse of second triangle represents √3 .

Draw the arc of  radius equal to the hypotenuse of second trinagle to get √3 on number line as shown in figure.