Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

NEET Class neet Answered

HELP
question image
Asked by astutijoshi | 28 Jul, 2019, 16:01: PM
answered-by-expert Expert Answer

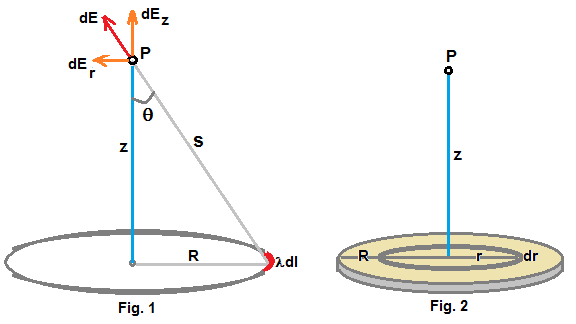
Fig.1 shows a charged ring of radius R that has charge density λ per unit length.
We need to find elecrical intensity at a point P which is on the axis passing through centre of ring and at a distance z from the centre.
we consider a small length dl in the ring that has charge λdl. Direction of electric field dE is shown in figure.
 
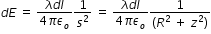begin mathsize 12px style d E space equals space fraction numerator lambda d l over denominator 4 pi epsilon subscript o end fraction 1 over s squared space equals space fraction numerator lambda d l over denominator 4 pi epsilon subscript o end fraction fraction numerator 1 over denominator open parentheses R squared space plus space z squared close parentheses end fraction end style ................................. (1)
 
  Electric field dE can be resolved in axial direction as dEz and radial direction dEr as shown infigure.
 
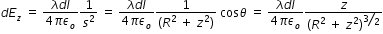
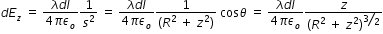
Axial field : begin mathsize 12px style d E subscript z space equals space fraction numerator lambda d l over denominator 4 pi epsilon subscript o end fraction 1 over s squared space equals space fraction numerator lambda d l over denominator 4 pi epsilon subscript o end fraction fraction numerator 1 over denominator open parentheses R squared space plus space z squared close parentheses end fraction space cos theta space equals space fraction numerator lambda d l over denominator 4 pi epsilon subscript o end fraction z over open parentheses R squared space plus space z squared close parentheses to the power of begin display style bevelled 3 over 2 end style end exponent end style
 
When we add the electric field due to whole ring by integration, Radial component will be cancelled out.
 
Hence Electric field of whole charged ring at a point P = begin mathsize 12px style integral d E subscript z space equals space space integral fraction numerator lambda d l over denominator 4 pi epsilon subscript o end fraction z over open parentheses R squared space plus space z squared close parentheses to the power of begin display style bevelled 3 over 2 end style end exponent space equals space fraction numerator 2 pi R space lambda over denominator 4 pi epsilon subscript o end fraction z over open parentheses R squared space plus space z squared close parentheses to the power of begin display style bevelled 3 over 2 end style end exponent end style ..................(2)
In the above eqn.(2), 2πRλ in the numerator is the total charge on the ring.
 
Now let us calculate electric field due to a circular disc of radius R that has charge density σ per unit area.
Fig.2 shows such a disc. Let us consider a ring which is part of disc that has radius r, thickness dr as shown in figure.
 
Using eqn.(2), we get the electric field dE due to this ring at a point P which is at a distance z from centre of disc is given by
 
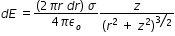begin mathsize 12px style d E space equals fraction numerator open parentheses 2 pi r space d r close parentheses space sigma over denominator 4 pi epsilon subscript o end fraction z over open parentheses r squared space plus space z squared close parentheses to the power of begin display style bevelled 3 over 2 end style end exponent end style ..........................(3)
Electric field due to charged disc is obtained by integrating above eqn.(3).
 
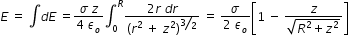begin mathsize 12px style E space equals space integral d E space equals fraction numerator sigma space z over denominator 4 space epsilon subscript o end fraction integral subscript 0 superscript R fraction numerator 2 r space d r over denominator open parentheses r squared space plus space z squared close parentheses to the power of begin display style bevelled 3 over 2 end style end exponent end fraction space equals space fraction numerator sigma space over denominator 2 space epsilon subscript o end fraction open square brackets 1 space minus space fraction numerator z over denominator square root of R squared plus z squared end root end fraction close square brackets end style ........................(4)
From eqn.(4), by substituting σ = 10 nC/m2 , R = 4 cm and z = 3 cm,  we get electric field E = 0.226×103 N/C
Answered by Thiyagarajan K | 29 Jul, 2019, 07:43: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
NEET neet - Physics
what is meant by projectile
Asked by sayrapatelsp09 | 04 Dec, 2024, 20:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
3 masses of 16 kg and 8 kg and 4 kg are placed in contact as shown in the figure if a force of 140 newton is applied on 4 KG mass, then the force on 16kg will be
Asked by jhansikethburugu2008 | 04 Oct, 2024, 22:09: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
RMS velocity for certain di atomic at 27°c is 1930 find the gas
Asked by arfasamreen7766 | 13 Sep, 2024, 16:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
at thin wire has length of 21.7cm and radius 0.46mm calculate the volume of the wire to connect significant figures
Asked by mehekfz8738 | 02 Sep, 2024, 19:56: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
explain nature of magnetic field lines
Asked by muhammadifatimanoori | 22 Aug, 2024, 09:10: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
a parallel plate capacitor is charged up to a potential V distance between the plates is d. electric field intensity between the plates is E. if the distance between plates is doubled then the electric field will be
Asked by kumawatranya0812 | 16 Aug, 2024, 16:25: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
hailstones fall from a certain height if only 1% of the hailstones melt on reaching the ground find the height from which they fall
Asked by nzf1042692 | 10 Aug, 2024, 21:07: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
The position function of a particle moving along the x axis is x(t t 2 3t 2) time t=0 to t =3 find distance travelled
Asked by dropper744 | 08 Aug, 2024, 10:44: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
Ek pahiya 120 Chakkar Prati minut se ghoom raha hai to ghumte pahiye ki koniya Sal Hogi
Asked by sajnadevirrc | 06 Aug, 2024, 11:55: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
NEET neet - Physics
dimensional formula of heat energy
Asked by nainamalviya833 | 04 Aug, 2024, 20:42: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt