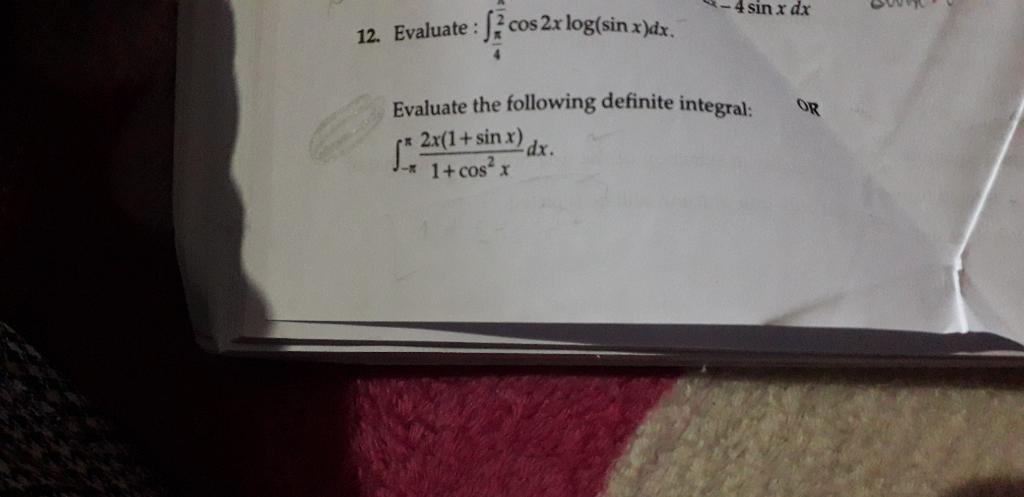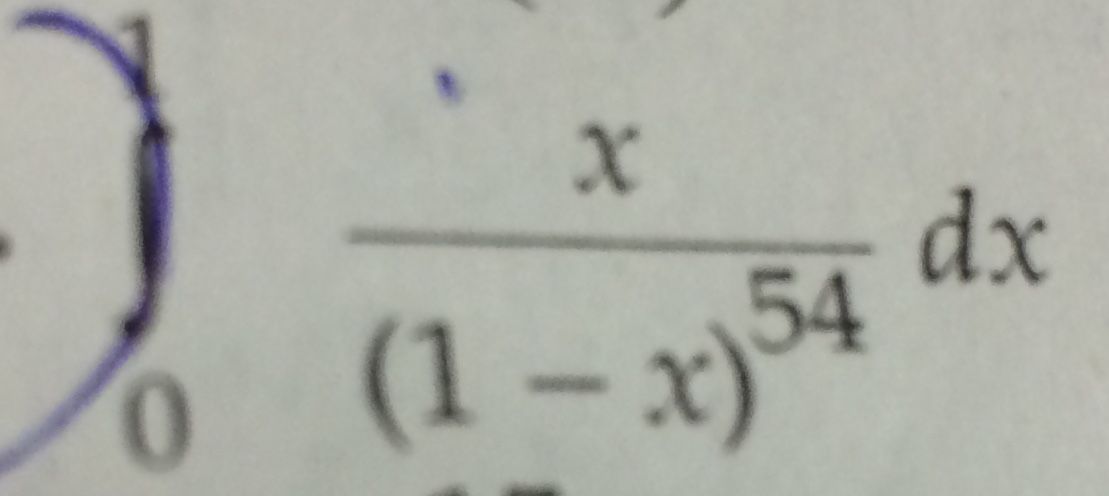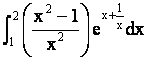CBSE Class 12-science Answered
Find 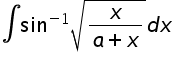
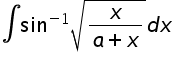
Asked by sunil2791 | 04 Jul, 2017, 06:35: AM

Answered by Sneha shidid | 04 Jul, 2017, 10:02: AM
Concept Videos
CBSE 12-science - Maths
Asked by lovemaan5500 | 07 Feb, 2020, 09:50: AM
CBSE 12-science - Maths
Asked by Harshgupta343260 | 25 Aug, 2019, 05:18: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 01 Oct, 2014, 04:44: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM