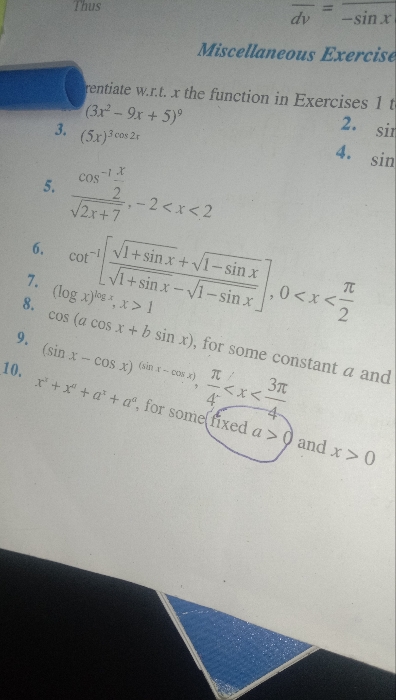CBSE Class 12-science Answered
evaluate
Asked by | 03 Jan, 2010, 06:21: PM
Expert Answer
sinx/(sinx+cosx) = 1/(1+cotx) = tanx/(1+tanx)
Put tanx = y
sec2x dx = dy
(1+tan2x)dx = dy
dx = dy/(1+tan2x)
dx = dy/(1+y2)
sinx dx/(sinx+cosx) = y dy/{(1+y)(1+y2)}
= (1/2){(y+1) dy/(1+y2)} - (1/2)dy/(1+y)
= (1/2)(1/2)ln(1+y2) + (1/2) tan-1y - (1/2)ln(1+y) + c
= (1/4)ln(1+y2) + (1/2) tan-1y - (1/2)ln(1+y) + c
= (1/4)ln(sec2x) + (x/2) - (1/2)ln(1+tanx) + c
= ln(
(secx/(1+tanx) + x/2 + c.
Regards,
Team,
TopperLearning.
Answered by | 03 Jan, 2010, 10:04: PM
Application Videos
-
ProblemsbasedonIntoFunction-I
Video contains the question based on verification of a function to be Into ... -
ProblemsbasedonIntoFunction-II
Video contains the question based on verification of a function to be Into ...
Concept Videos
-
Properties of Inverse Trigonometry Part - 1
This video explains the properties of inverse trigonometric applications an... -
Graphical representation of inverse trigonometric funct ...
Graphical representation of inverse trigonometric functions and principle ... -
Continuous and Discontinuous function
Understand the meaning of function to be continuous and discontinuous, comb... -
Relationship between continuity and differentiability - ...
Relationship between continuity and differentiability, concept of composite... -
Introduction to Relations
This video explains the concept of relations and types of relation like Emp...
CBSE 12-science - Maths
Asked by leelasri11663 | 25 Apr, 2024, 11:34: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by aishaazmata | 24 Apr, 2024, 08:48: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by revengesena | 24 Apr, 2024, 06:08: PM
ANSWERED BY EXPERT
CBSE 12-science - Maths
Asked by mahammadsharifdakhani67 | 16 Apr, 2024, 07:43: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by 20muskaansharma23 | 08 Apr, 2024, 11:31: AM
ANSWERED BY EXPERT
CBSE 12-science - Maths
Asked by cherrycharishma512 | 01 Apr, 2024, 12:32: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by annapoornaa429 | 31 Mar, 2024, 08:23: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by shirishakuruva477 | 28 Mar, 2024, 09:52: PM
ANSWERED BY EXPERT
