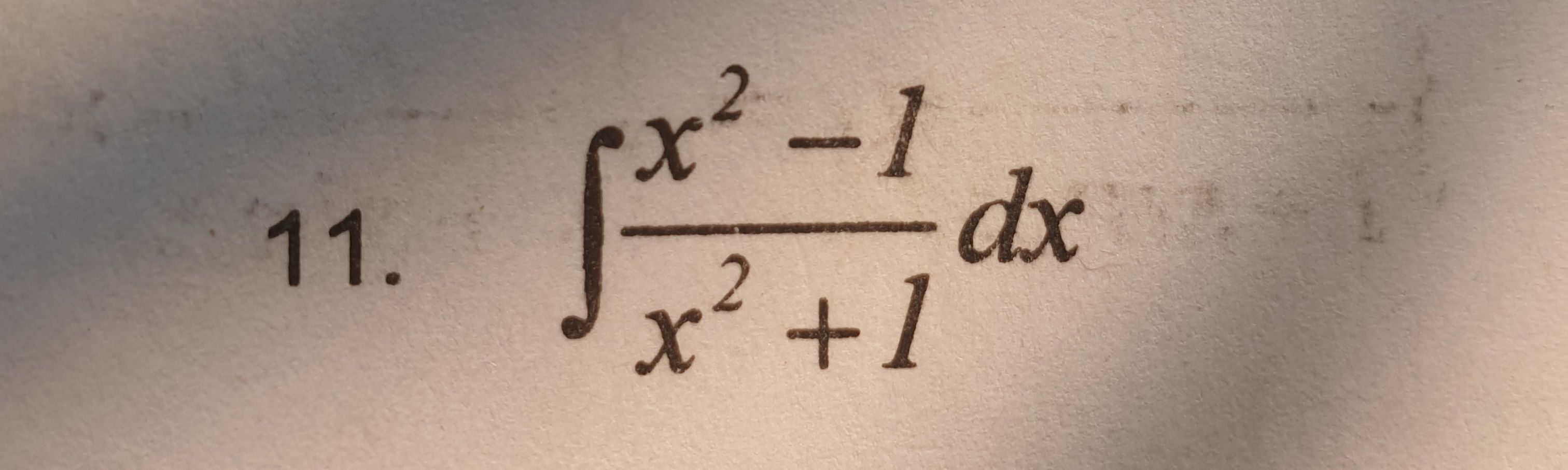CBSE Class 12-science Answered
Evaluate: 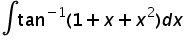
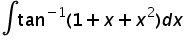
Asked by Kaustav Mondal | 27 Sep, 2014, 11:02: PM
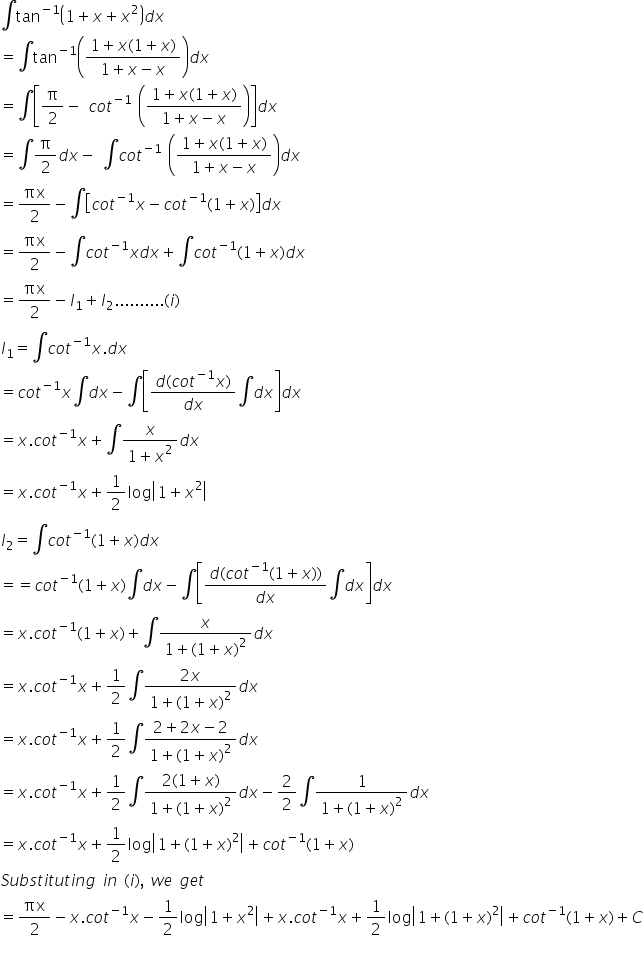
Answered by Prasenjit Paul | 29 Sep, 2014, 11:01: AM
Concept Videos
CBSE 12-science - Maths
Asked by Brahmduttkumar5102003 | 01 Jan, 2021, 01:44: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 28 Oct, 2016, 01:07: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 28 Oct, 2016, 01:09: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM