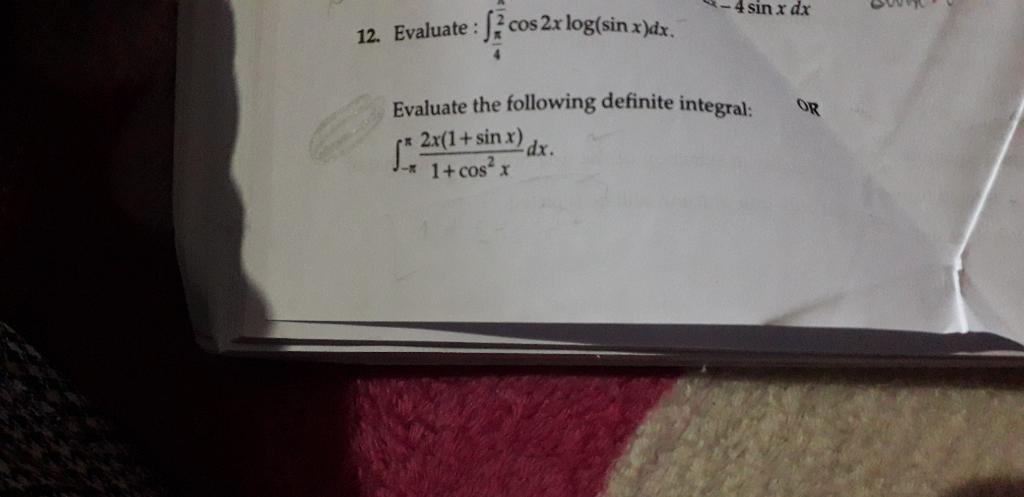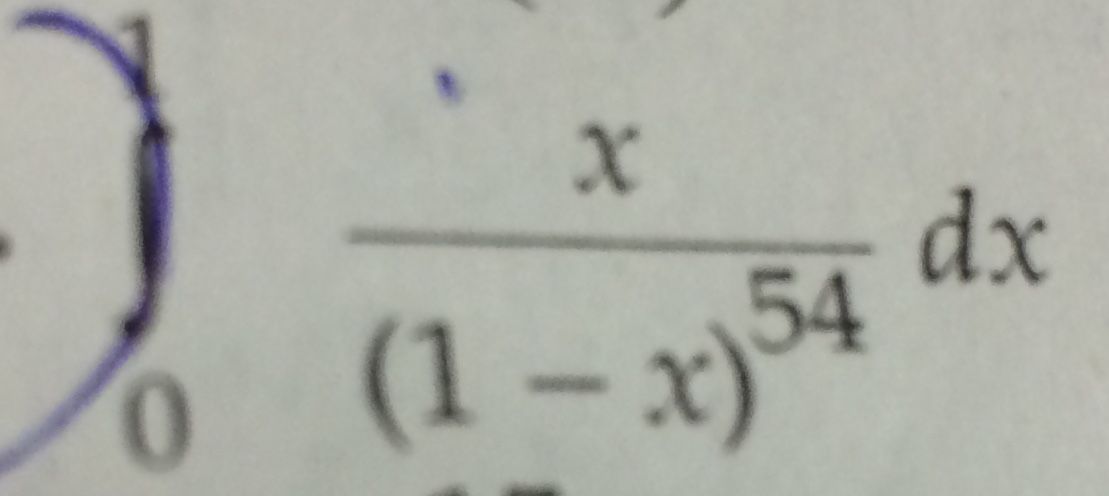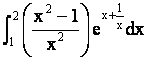CBSE Class 12-science Answered
Evaluate : 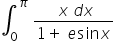 ,
, 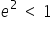
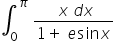 ,
, 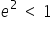
Answer is 

Asked by ahuja8087 | 15 Mar, 2017, 04:54: PM

Dear student, the answer is as shown above. Kindly check. Since this is a definite integral so it should have a constant answer rather than that in terms of x.
Answered by Rebecca Fernandes | 16 Mar, 2017, 02:21: PM
Concept Videos
CBSE 12-science - Maths
Asked by lovemaan5500 | 07 Feb, 2020, 09:50: AM
CBSE 12-science - Maths
Asked by Harshgupta343260 | 25 Aug, 2019, 05:18: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 01 Oct, 2014, 04:44: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM