Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

Mizoram Class 9 Answered

Derive the equation of motion of a body in uniform acceleration using graphical method
Asked by mateilrf | 19 Jan, 2021, 10:25: PM
answered-by-expert Expert Answer
Acceleration a is defined as rate of change of velocity.
 
If at initial time to , let the velocity be u and after time t , let the velocity be v. 
 
Acceleration a = ( v - u ) / ( t - to )   ..................(1)
 
If acceleration is uniform then a is constant with respect to time. 
 
From eqn.(1) , we get v =  u + a ( t - to ) .................(2)
 
Let us consider we start recording time from reference time instant to , so that we consider to = 0
 
Hence we get velocity as a function of time as , v = u + a t  ...................(3)
 
Graph of eqn.(3) that gives velocity as a function of time is linear and it is given below
 
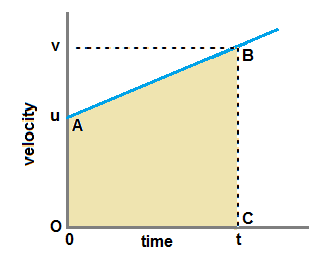
Area under the velocity-time graph between time τ =0 to time τ = t is the distance travelled by the object in time duration of t seconds.
 
As seen from graph given above, area under the graph between time τ = 0 to time τ = t is a trapezium OABC
 
Area of trapezium OABC = (1/2) [ OA + BC ] × OC  ......................(4)
 
OA = inital velocity  u  ;  BC = final velocity v  ; OC = time duration t 
 
Hence eqn.(4) becomes ,   Area OABC = (1/2) [ u+v ] × t
 
If S is distance travelled by object in time duration t , then above equation becomes ,  
 
S = (1/2) [ u+v ] × t ........................(5)
 
If we substitute final velocity v from eqn.(3) , we get , S = (1/2) [ u + u + a t ] × t 
 
Hence we get , S = u + (1/2) a t2 .........................(6)
 
If we want to eliminate t from eqn.(5) , we use eqn.(3) to substitute t as , t = ( v-u) /a ............(7)
 
Using eqn.(7) , we rewrite eqn.(5) as 
 
S = (1/2) [ u + v ] ( v - u ) /a   or     v2 = u2 + ( 2 a S )   ............................(8)
 
Eqn.(3) , Eqn.(6) and Eqn.(8) are equations of motion if acceleration is uniform 
 
v = u + a t  .................................(3)
 
S = u + (1/2) a t2 .........................(6)
 
v2 = u2 + ( 2 a S )   ......................(8)
Answered by Thiyagarajan K | 20 Jan, 2021, 10:36: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
Mizoram 9 - Physics
Derive the equation of motion of a body in uniform acceleration using graphical method
Asked by mateilrf | 19 Jan, 2021, 10:25: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×