Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

JEE Class main Answered

A massive rod of length 1m is placed on a smooth horizontal surface is pulled longitudinally by a force of 10N as shown in figure. The tension in rod varies as T=10√x.How will linear mass density vary with x?
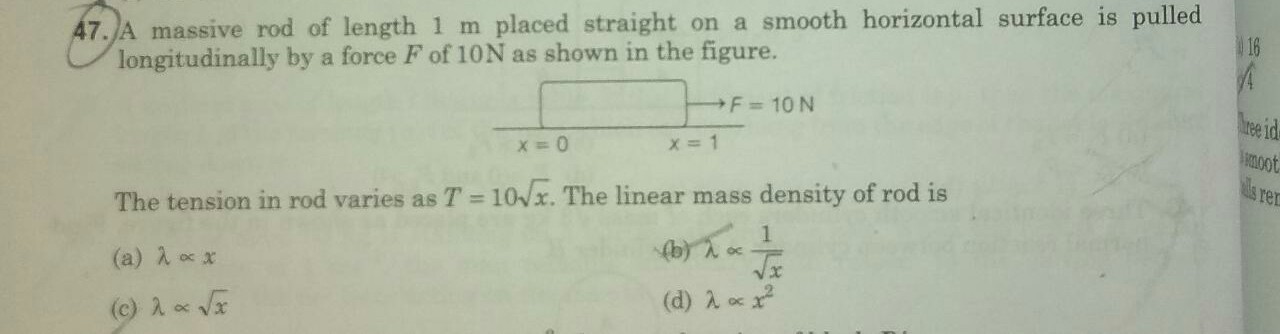
question image
Asked by mailkunalmunjal | 09 Sep, 2020, 06:19: AM
answered-by-expert Expert Answer
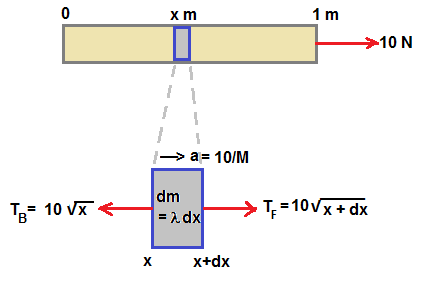
Let a massive rod of 1 m length is subjected to a force 10 N as shown in figure. Let M be the mass of rod. 
 
Acceleration a of whole rod = Force / mass = ( 10 / M )
 
let us consider a small mass element dm at a distance x and having width dx.
 
Tension forces acting at forward and backward direction are shown in figure .
 
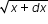
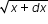
Forward direction tension force , TF = 10 begin mathsize 12px style square root of x plus d x end root end style 
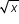
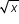
Backward direction tension force, TB = 10 begin mathsize 12px style square root of x end style
By Newton's second law,  TF - TB = dm × a
 
Hence we have , 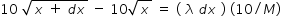begin mathsize 14px style 10 space square root of x space plus space d x end root space minus space 10 square root of x space equals space left parenthesis space lambda space d x space right parenthesis space left parenthesis 10 divided by M right parenthesis end style 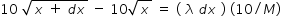 ................(1)
where λ is linear mass density.
 
After simplification , eqn.(1) can be written as
 
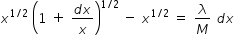
begin mathsize 14px style x to the power of 1 divided by 2 end exponent space open parentheses 1 space plus space fraction numerator d x over denominator x end fraction close parentheses to the power of 1 divided by 2 end exponent space minus space x to the power of 1 divided by 2 end exponent space equals space lambda over M space d x end style
begin mathsize 14px style x to the power of 1 divided by 2 end exponent space open parentheses 1 space plus space 1 half fraction numerator d x over denominator x end fraction close parentheses space minus space x to the power of 1 divided by 2 end exponent space equals space 1 half space fraction numerator d x over denominator x to the power of 1 divided by 2 end exponent end fraction space equals space lambda over M space d x end style
Hence , λ = ( M/2 ) ( 1 / √x )
 
Hence linear mass density λ begin mathsize 14px style proportional to end style ( 1 / √x )
Answered by Thiyagarajan K | 15 Oct, 2020, 23:47: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
JEE main - Physics
What is circular motion
Asked by jwjwwj | 16 Jan, 2025, 13:26: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
what is difference between drift and jerk
Asked by mishradarshan03 | 22 Dec, 2024, 11:45: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
a marble block of mass 2 kg lying on ice when a given velocity of 6 ms–1 is stopped by friction in 10 seconds then co efficient of friction is
Asked by sumalathamadarapu9 | 23 Oct, 2024, 22:06: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
show that the frequency of oscillations remain unchanged whether a mass attached to a spring is made to oscillate in the vertical or in the horizontal direction
Asked by py309649 | 13 Oct, 2024, 13:39: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Square of the time period of revolution of a planet is proportional to the cube of the mean distance between sun and planet. If mean distance is increased by 2% then percentage change in its time period is
Asked by coolskrish | 13 Oct, 2024, 12:50: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
two particles of mass m and 4m are initially actress the sad moving towards each other due to mutual gravitational force at an instantly of m is vî then at this instant the velocity of mass 4m is
Asked by midnightmoon3355 | 09 Oct, 2024, 09:09: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
what is the second law of thermodynamics
Asked by rambabunaidu4455 | 03 Oct, 2024, 16:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
what is the relation between drift velocity and mobility
Asked by ratchanavalli07 | 17 Sep, 2024, 07:46: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
A ball of mass m approaches a moving wall of infinite mass with speed v along the normal to the wall. The speed of the ball is u towards the ball. The speed of the ball after elastic collision with the wall is
Asked by yayashvadutta45 | 15 Sep, 2024, 19:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
a current of 2a is flowing through a conductor of length 22m bent in arc radius 5cm
Asked by adithireddy999 | 03 Sep, 2024, 09:35: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt