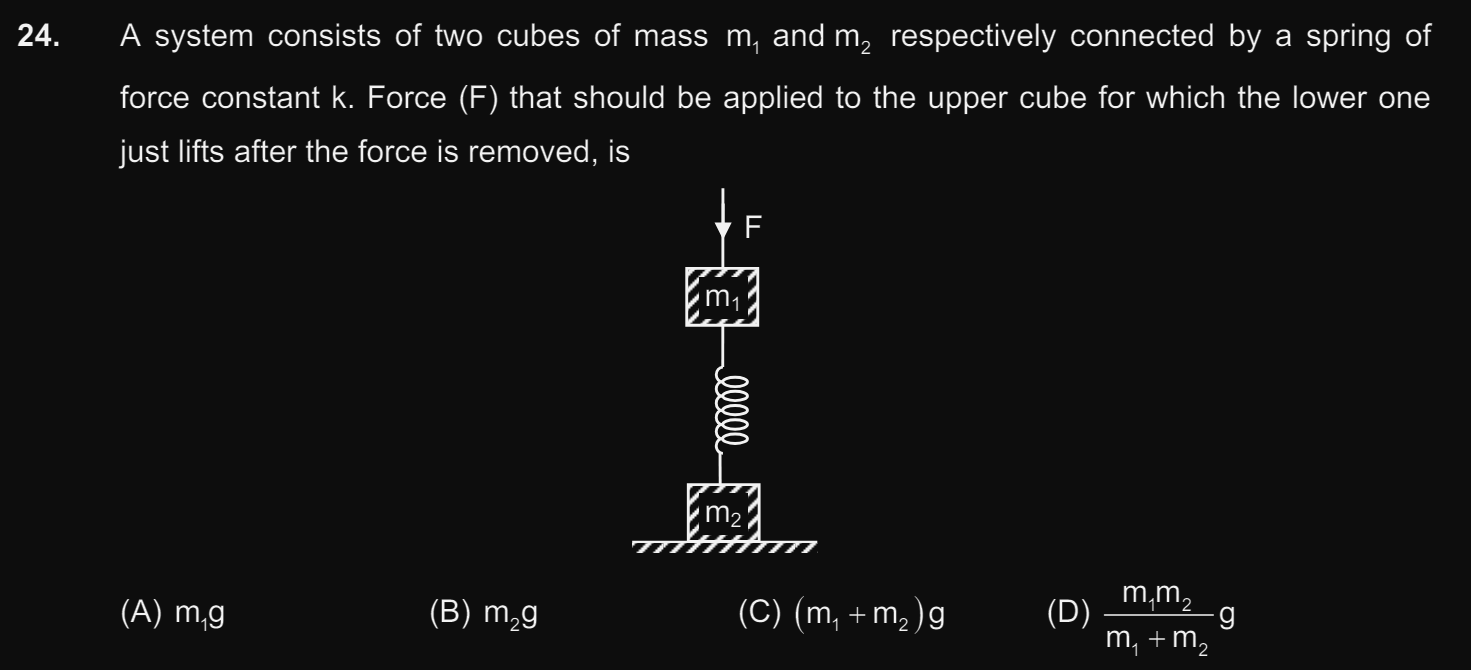
Doubts and Solutions
OR
JEE Main - Physics
Asked by ashwinskrishna2006 | 07 May, 2024, 05:33: PM
CBSE VIII - Science
Asked by sppatil3668 | 07 May, 2024, 05:29: PM
CBSE XII Commerce - Accountancy
Asked by riyanprajapati308 | 07 May, 2024, 05:01: PM
CBSE XI Science - Physics
Asked by rajeshabirami27 | 07 May, 2024, 04:31: PM
Foundation X - Maths
Asked by arushanaseer | 07 May, 2024, 01:08: PM
JEE Main - Chemistry
Asked by jayshreebhalerao7 | 07 May, 2024, 08:24: AM